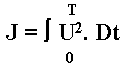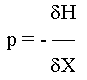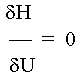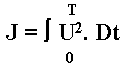ELEKTRO INDONESIA
Edisi ke Dua Belas, Maret 1998
Aplikasi Sistem Kontrol
Optimal dalam Reaktor Nuklir
Sistem kontrol merupakan sebuah sistem
yang terdiri atas satu atau beberapa peralatan yang berfungsi untuk mengendalikan
sistem lain yang berhubungan dengan sebuah proses. Dalam suatu industri,
semua variabel proses seperti daya, temperatur dan laju alir harus dipantau
setiap saat. Bila variabel proses tersebut berjalan tidak sesuai dengan
yang diharapkan, maka sistem kontrol dapat mengendalikan proses tersebut
sehingga sistem dapat berjalan kembali sesuai dengan yang diharapkan. Sistem
kontrol dapat digunakan di dalam pabrik, gedung-gedung maupun dalam PLTN.
Sistem kontrol sudah berkembang sejak
awal abad ke 20, yaitu dengan ditemukannya sistem kontrol proporsional,
integral dan sistem kontrol differensial. Dalam perkembangannya, ketiga
sistem kontrol tersebut digabung menjadi satu, menjadi sistem kontrol PID
( Proporsional, Integral, Differensial ).
Untuk mengendalikan sistem proses
yang sangat komplek, seperti PLTN dan jaringan distribusi listrik terpadu,
maka sistem kontrol PID mempunyai banyak kelemahan. Sistem kontrol PID
hanya dapat digunakan untuk sistem proses yang berbentuk linier dengan
satu masukan dan satu keluaran ( SISO ). Untuk mengatasi hal ini, maka
dikembangkan sistem kontrol yang lebih canggih, yaitu sistem kontrol optimal.
Sistem Kontrol Optimal
Yang dimaksud dengan optimal yaitu hasil
paling baik yang dapat dicapai dengan memperhatikan kondisi dan kendala
dari sistem tersebut. Dalam sistem kontrol optimal, maka istilah optimal
seringkali merujuk pada minimal. Misalnya meminimalkan bahan bakar (input),
waktu dan kesalahan (error).
Supaya sistem proses tersebut dapat
dikontrol, maka perlu dibuat model matematis yang menghubungkan antara
masukan (input), proses dan keluaran (output). Pada sistem kontrol optimal,
model yang banyak digunakan adalah model persamaan keadaan. Dalam persamaan
keadaan, persamaan differensial dari sistem yang semula berorde n diubah
menjadi n persamaan differensial berorde satu secara simultan dan ditulis
dalam notasi vektor matrik. Metode persamaan keadaan banyak digunakan dalam
menganalisis suatu sistem, karena metode tersebut mempunyai banyak keuntungan
yaitu:
-
Notasinya mudah dan kompak, dan dapat
dibentuk ke dalam persamaan matrik dan vektor.
-
Notasinya seragam untuk semua sistem
tanpa mempedulikan tingkat, maka dapat diselesaikan dengan menggunakan
teknik algorithma dan komputer dengan mudah.
-
Dapat digunakan untuk mengetahui karakteristik
dan tingkah laku sistem secara lebih lengkap.
Dengan menggunakan model persamaan keadaan,
maka sistem kontrol optimal dapat diterapkan pada sistem proses yang komplek.
Sistem kontrol optimal dapat digunakan untuk mengendalikan sistem proses
yang berbentuk linier maupun non linier Sistem kontrol optimal juga dapat
digunakan untuk mengontrol sistem proses dengan banyak masukan dan banyak
keluaran (MIMO).
Bentuk umum dari persamaan keadaan
adalah sebagai berikut:
X = A.X + B.U
X= variabel keadaan.
U = input ( masukan ).
A = matrik yang mempengaruhi harga
variabel keadaan.
B = matrik yang mempengaruhi harga
masukan.
Masalah umum dalam perancangan suatu
sistem kontrol adalah pencapaian spesifikasi rancangan yang telah ditentukan.
Hal lain yang juga perlu diperhatikan adalah bagaimana spesifikasi rancangan
ini dapat dicapai. Sistem kontrol yang baik adalah sistem kontrol yang
mempunyai daya tanggap yang cepat dan stabil, tetapi tidak memerlukan energi
yang berlebihan. Sistem kontrol demikian dapat dicapai melalui pengaturan
indeks performansi yang tepat. Sistem kontrol yang dirancang berdasarkan
optimasi indeks performansi disebut sistem kontrol optimal.
Indeks performansi suatu sistem kontrol
optimal merupakan indikator dari kumpulan deviasi suatu sistem dari keadaan
ideal atau keadaan yang diinginkan. Indeks performansi dapat digunakan
untuk meminimalkan energi, kesalahan dan waktu. Bila hanya bagian tertentu
dari sistem yang akan dioptimalkan, maka indeks performansinya dipilih
sesuai dengan bagian yang akan dioptimalkan tersebut. Bentuk umum dari
indeks performansi adalah sebagai berikut:
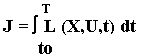
J = indeks performansi.
L (X,U,t) = fungsi kuadratik dari
X, U dan t
t = waktu
Pada sistem kontrol optimal, optimasi
kontrol dicapai dengan meminimalkan nilai indeks performansi tersebut.
Ada beberapa metode yang dapat digunakan untuk meminimalkan indeks performansi
yaitu:
Kalkulus variasi: digunakan untuk
mengoptimalkan sistem proses yang sederhana.
-
Persamaan aljabar Riccati: digunakan
untuk mengoptimalkan sistem proses yang
berbentuk linier.
-
Persamaan Hamilton Pontryagin: dapat
digunakan untuk mengoptimalkan sistem proses yang berbentuk linier mupun
non linier
Dinamika Reaktor Nuklir
Reaktor nuklir merupakan tempat untuk
mengadakan reaksi fisi (pembelahan).
Bahan bakar yang biasa digunakan
adalah Uranium yang merupakan zat radio aktif. Operasi reaktor dilakukan
dengan jalan memberikan neutron kedalam bahan bakar sehingga terjadi reaksi
fisi. Dari reaksi fisi tersebut dihasilkan neutron, energi yang sangat
besar dan inti -inti baru yang tidak stabil. Dengan adanya neutron-neutron
baru tersebut, maka reaksi fisi dapat dilanjutkan sehingga terjadilah reaksi
berantai. Pada reaktor riset, neutron yang dihasilkan digunakan untuk penelitian,
sedangkan energinya dibuang. Dalam reaktor daya ( reaktor untuk PLTN ),
energi yang dihasilkan digunakan untuk memutar turbin sehingga dihasilkan
tenaga listrik yang sangat besar.
Untuk model reaktor titik, dimana
fluks neutron tidak bergantung pada tempat dan energi neutron berada dalam
satu kelompok, maka dapat dibuat persamaan keadaan dinamika reaktor sebagai
berikut:
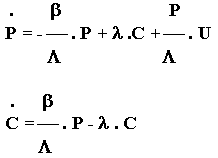
P = daya
C = precursor
b = fraksi neutron kasip
L = umur generasi neutron
l = konstanta peluruhan neutron
U = input ( masukan ).
Karena daya reaktor dan precursor
dari waktu ke waktu selalu berubah, maka daya reaktor dan precursor merupakan
variabel keadaan. Jadi P = X1 dan C = X2.
Maka persamaan di atas dapat ditulis
dalam bentuk persamaan keadaan sebagai berikut:
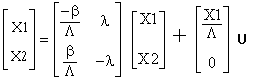
Dengan menggunakan harga awal sebagai
berikut:
-
X1(0) = 10 Watt
-
X2(0) = 0
-
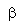 = 0,0073
= 0,0073
-
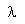 = 0,0768
detik -1
= 0,0768
detik -1
-
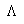 = 0,00096
detik
= 0,00096
detik
-
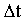 = 0,5
detik.
= 0,5
detik.
-
U = 0,0539
Maka besarnya kenaikan daya reaktor
sebagai fungsi waktu dapat dihitung dengan menggunakan program matlab.
Hasil perhitungan tersebut dapat dilihat pada tabel I. Dalam percobaan
ini, optimasi hanya dilakukan pada harga masukan. Jadi indeks performansi
yang diperlukan untuk menaikkan daya reaktor dari 10 Watt ke 1000 Watt
adalah sebagai berikut:
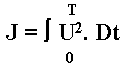
J = 0,0378 .
|
Nomor
|
Waktu (detik)
|
Daya (Watt)
|
0
1
2
3
4
5
6
7
8
9
10
11
12 |
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
5,5
6
|
10
14
21
32
47
69
102
151
222
328
484
711
1000
|
Tabel I
Kenaikan daya reaktor sebagai fungsi
waktu
Optimasi Daya Reaktor
Persamaan dinamika reaktor merupakan
persamaan keadaan non linier. Untuk mengoptimalkan daya reaktor maka dapat
digunakan persamaan Hamilton Pontryagin. Persamaan Hamilton Pontryagin
merupakan pengembangan dari persamaan Kalkulus variasi, teknik Multiplikasi
Lagrange dan persamaan Euler. Persamaan Hamilton Pontryagin dapat digunakan
untuk mengoptimalkan sistem proses yang bersifat komplek dengan banyak
kendala. Persamaan Hamilton Pontryagin juga dapat digunakan untuk mengoptimalkan
sistem proses yang bersifat linier maupun non linier.
Langkah-langkah untuk mengoptimalkan
daya reaktor dengan menggunakan persamaan Hamilton Pontryagin adalah sebagai
berikut:
-
Persamaan Hamilton Pontryagin:
H(X,U,p,t) = L(X,U,t) + pt
(A.X + B.U)
-
Persamaan Costate:
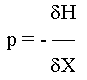
-
Kondisi Stasioner:
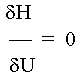
Dengan menggunakan beberapa persamaan
diatas, maka besarnya kenaikan daya reaktor sebagai fungsi waktu setelah
dioptimalkan dapat dihitung dengan menggunakan program matlab. Hasil perhitungan
tersebut dapat dilihat pada tabel II. Karena yang dioptimalkan hanya masukan
, maka indeks performansi yang diperlukan untuk menaikkan daya reaktor
dari 10 Watt ke 1000 Watt dapat dihitung dengan rumus sebagai berikut:
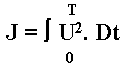
J = 0,00588.
|
Nomor
|
Waktu (detik)
|
Input
|
Daya (Watt)
|
0
1
2
3
4
5
6
7
8
9
10
11
12 |
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
5,5
6
|
0,0083
0,0094
0,0104
0,0116
0,0128
0,0140
0,0155
0,0172
0,0196
0,0231
0,0287
0,0383
0,0573 |
10
11
11,7
13,6
17
22
30
41
63
104
190
403
1000
|
Tabel II
Kenaikan daya reaktor sebagai fungsi
waktu setelah dioptimalkan.
Kesimpulan
Dari uraian diatas maka dapat ditarik
kesimpulan sebagai berikut:
-
Dengan menggunakan persamaan Hamilton
Pontryagin, maka indeks performansi yang diperlukan untuk menaikkan daya
reaktor dapat diperkecil. Jadi persamaan Hamilton Pontryagin dapat digunakan
untuk mengoptimalkan daya reaktor.
-
Dalam sistem kontrol optimal, persamaan
yang digunakan untuk memodelkan sistem proses adalah persamaan keadaan.
Dengan demikian maka semua variabel keadaan dari sistem proses dapat dipantau
dan harganya dapat diketahui setiap saat.
-
Sistem kontrol optimal dapat digunakan
untuk mengendalikan sistem proses yang bersifat MIMO ( Multi Input Multi
Output ), yaitu sistem proses dengan banyak masukan dan banyak keluaran.
Sedangkan sistem kontrol klasik tidak dapat digunakan untuk mengendalikan
sistem proses yang demikian.
-
Dengan semakin kompleknya industri seperti
PLTN dan jaringan distribusi listrik, maka sistem kontrol yang canggih
sangat diperlukan. Dengan demikian maka sistem kontrol optimal perlu dikembangkan
karena mempunyai prospek yang baik dimasa yang akan datang.
Daftar Pustaka
-
Brogan, W.L., Modern Control Theory
, Prentice-Hall, Inc., New Yersey, 1985.
-
Lewis, F.L., Optimal Control, John
Wiley & Sons,Inc., New York, 1985.
-
Lewis, E.E., Nuclear Power reactor
Safety, John Wiley & Sons, Inc., New York, 1977.
-
Hasan, Optimasi Reaktivitas pada
sistem pengaturan daya reaktor zero power dengan menggunakan persamaan
Hamilton Pontryagin,Tesis, ITB, Bandung, 1994.
Oleh: Ir. Hasan, MT
[[Sajian Utama] [Sajian
Khusus]
[KOMPUTER] [TELEKOMUNIKASI]
[ MULTIMEDIA ] [ENERGI]
[TUTORIAL]
Please send comments, suggestions, and criticisms about ELEKTRO
INDONESIA.
Click here to send me
email.
[ Halaman Muka]
© 1996-1998 ELEKTRO
Online.
All Rights Reserved.
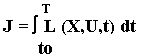
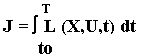
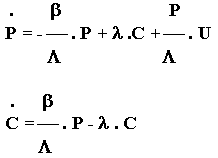
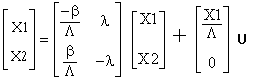
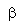 = 0,0073
= 0,0073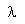 = 0,0768
detik -1
= 0,0768
detik -1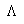 = 0,00096
detik
= 0,00096
detik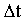 = 0,5
detik.
= 0,5
detik.