Probably everybody who knows quantum mechanics can sense
the same. It's a real pleasure by the way. Words emit other virtual words just like electron emits virtual photons.

  Since our brain behaves like dynamic system  the words play
a role of quasi-particles and memory of the brain plays a role of vacuum which determines interaction constants of words.

Consider simple examples showing that quantum devices can solve problems better then classical ones:
Problem 1.
Suppose there is a number of channels between two cells.
Channels may be open, or closed.
Problem  to solve is to clear up whether or not any open channel exists.
In classical case one has  to insert particles to the inputs of all channels and search for the particles at output.
In quantum case it's enough to send one particle propagating through all channels.
If at least one channel is open the particle will appear at the output.

Problem 2.
Let be a cell connected by many channels to other cells.
It's known that only one of channels is open. How to find
the open channel ?
In classical case we again send particles through all channels.
In quantum  case we send one particle. The answer is the
destination cell in which the particle will appear.

3.  st connectivity and graph-traversing automata:
   Given an undirected graph G and two distinguished vertices
s and t, determine if there is a path from s to t.
   Quantum device solving this problem consists of nodes or cells
connected by channels according to graph given.
We insert a particle in node s and after some time measure
the particle presence in node t. In quantum case a particle
passes all possible trajectories in parallel.
In classical case one can try the same procedure, but a lot of particles
needed to pass all possible paths.

-------------------------------

  A formal language is usually defined as a set of sentences which can be derived using a certain set of rules or generated by an automaton.
  In QLT a language consists of sentences which can be generated by a memory considered.
Generated means that words of a sentence interact strongly in a memory exciting long lived states in it.

    Process of recognition and generation of words is probably similar to
the process of quantum mechanical scattering. It explains how we can look through all our memory so fast as we do, since quantum mechanical search goes in parallel.

   A word really is a sort of "bare" word plus all its interactions with other words and objects stored in a human memory. Word stimulation results in excitation of  its links producing under suitable conditions the long lived quasi stationary states of brain which include many words.
    A word as though sits in a "potential" created by other words.
Like in quantum field theory one can define  the mutual potential energy of two words as the total propagation amplitude squared. The total propagation amplitude is the sum of propagation amplitudes taken over all possible  links between these words.  All possible means that all semantic networks, images and models containing links between the words  are taken into account.
In a particular case only the links from selected models may participate.

  Let’s consider a set of neurons nk (see the picture).   Every neuron has many inputs and one output.  Index  k numbers neurons, index j numbers the inputs.  In neuron nkevery input j has a connection weight wj(k)  . Let’s consider  how this set of neurons can recognize input vectors in classical and quantum mechanical case.

 In process of education a set of  input vectors  forms the weights.  Every vector comes to one (and only one) neuron. Components of the vector correspond to neuron inputs.  In neuron k the weights wj(k) which are proportional to the  vector vj(k) components are formed.

  In process of recognition an arbitrary vector vj comes to all neurons in parallel.   Suppose that output of a neuron is proportional to the scalar  product s(k) of the input vector vj and vector of weights wj(k).  Then the maximal output will be in the neuron which weights are similar to the input vector.  The negative feedback between neurons helps to amplify the maximal signal and suppress others.

Consider simple mathematical model.  Let the neuron outputs qk change according to the following equations.

 (1)           d/dt (qk)  =  (qk) * sum(j) vjwj(k) - sum(k) (qk)*(qk) ;

Here  the first term gives linear amplification, second term - negative feedback.
The whole is a process with mode competition. Modes here are the outputs qk.
The output  qk with max sum(j) vjwj(k) survives resulting in the exitation of a certain neuron.

Now about the difference between classical and quantum mechanics.
In classical case in process of recognition all signals coming in parallel to look
over all neurons must be real signals (current pulses or just classical particles).
It takes a lot of energy.

In quantum case we just let a quantum particle pass through all possible paths.
First we let the particle come to the neuron inputs with the probability amplitudes proportional to the input vector components  (vector we want to recognize).  For example, at every neuron input we emit particle with such amplitude.
   Then the neuron internal weights are now the amplitudes for particle to pass through  specific input channel.  Probability amplitude for the particle to come in a neuron will be the scalar product of the input vector and weight vector again.
Because all is going in parallel the quantum mechanical case has an advantage of saving energy.

In quantum case instead of equations (1) we get Shredinger equation

 (2) ih d/dt (qk)  =  (qk) * sum(j) wj(k)vj ;

where qk  - wavefunction. Now the scalar product sum(j) vjwj(k) determines the energy
level value at individual neuron.
Suppose that ions can transit between  the neurons and some reservoir. Then in case of underbarrier transition the transition probability exponentially depends on energy levels considered.
This exponential dependance gives us very sensitive method for maximum evaluation.

    Let's consider a common case of a system which reacts on inputs and produces outputs.
From input side there are an input amplitude  vj and a matrixWjk .  Together they give the probability amplitudes Ak = sum(j) wkjvj to excite a certain internal state k of the system.
From the output side there is another transition matrix Tlk  ,  which determines  the probability amplitude to excite a certain output l from a certain internal state k  .

Finally the probaility to exite output l is equal to  sum(jk) Tlk wkjvj .
 

From such point of view a human memory is a huge number of internal models.
Many of them  are looked through in parallel (due to quantum mechanical nature) to produce the result.

Let's stress that classical machine cannot do it, or better
say that can but with a lot of energy required.
This explains why human intellect  is more poweful than artificial one till now.
 

    Once more example:
Let's consider chains of objects (words, for example ) which can be linked.
Let’s number words  (objects) by index i. Two words ai and aj  can be connected by link Tij.
We can record such chains on a lattice of cells (neurons). Link between words will mean that signal (or particle in quantum case) can pass between cells. Index k will number the different chains recorded (see the picture).

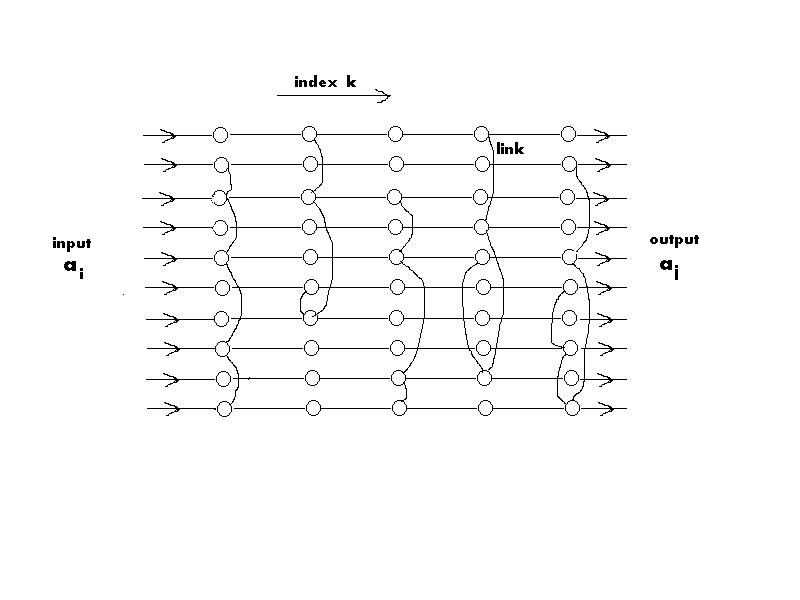
 A particle coming through input line i  will pass along any chain through the links existing in the chain. Total amplitude for particle to come to line j is the  sum of amplitudes over all chains recorded.
Such amplitude is large for those lines j which have many links with line i and small for other lines. Supposing that output signals are generated only for lines which are excited significantly we get what we need. Entering such a system an input word will excite or generate other words according to the chains previously recorded in the memory.

If particle (or particles) enters through several inputs (corresponding to combination of input words) then the total amplitude will be the sum of amplitudes for all inputs.
Again in quantum mechanical case all is going in parallel.

Suppose also that particle has a certain amplitude to tunnel between chains. Then the amount of paths which  particle  can pass increases significantly since a path now can be composed from parts of different chains.
In classical case it takes a lot of signals and power to look over all these combinations.

    Now let's suppose  that the particles are bosons in an active media.
Then additional particles are produced  due to induced radiation like in a laser.
This process leads to amplification of particle propagation between nodes with larger mutual propagation amplitude.
   The process is similar to processes with mode competition taking place in biological systems and lasers.
 

    Let's   consider  interaction of words from path-integral point of view. Suppose that every word is a quantized field.
Again we have words ai  interacting through links Tij  which form a memory.
See the network picture above.
Interaction operator (part of Hamiltonian) is
  sum(k) { sum(i,j) aiai+ Tij(k)aj+   +  Herm. conj. }, where
ai , aj+ are annihilation and creation operators of word quantum (semilon).
An input word  i  comes at moment t0 and excites (creates) other words through possible links Tij(k).
If we do time slices t1, t2, t3 ...  we shall see some word quanta excited at moment t1,
others at moment t2 and so on. This is the path integral picture usual for quantum field theory.
Every path has its probability amplitude.  The total amplitude to  excite an output word is the sum of amplitudes over all possible paths. When quanta considered are bosons in active media
they amplify their production like photons in a laser. As a result the modes with more branched links survive.
If the number of semantic networks enumerated by index k is large
the so called "classic" trajectories are possible which can be attributed to long lived quasi stationary states of the memory considered.

It's important that "classic" trajectories exist only if quantum memory is large enough.
This may be the possible explanation of human intellectual superiority over animals.

Probably in process of recording the links between cells which participate in long lived states are established better, like in usual neural networks.

------------------------------------
Quantum calculating device:
   To represent semantic networks we need a system (consisting of connected nodes or cells) in which many excitable chains can exist but one chain survives finally due to maximum weight of links along this chain.
   Consider two-dimensional grid, nodes are numbered by i, k .
Every grid row has a number of links T(i,j) (k) along x axis,
connecting nodes i and j of row k .
Note, that number of possible chains grows fast with the system
dimension growth because chains may include pieces of different
rows. So the search for the chain with maximum weight of links is
NP hard problem.
   To solve the problem let's introduce interaction between nodes i and j
of row k.
( c(i)c(j)+  + c(j)c(i)+  ) t(i,j) (k)+  - interaction operator.
where c(i) , c(i)+  - annihilation and creation operators for node i .
t(i,j) (k),  t(i,j) (k)+   - annihilation and creation operators of link T(i,j) (k).
Let's also allow transition between rows, to include in the game
the chains containing nodes of different rows.
Suppose t(i,j) (k) - bosons , and proccess run in pumped medium in
which t(i,j) (k) creation amplitude is larger than absorption amplitude.
Then we hope that exitation amplitude is larger for chains which includes more nodes connected by links t(i,j) (k) .

-----------------------

        About generalization in quantum mechanical networks.

  In classical neural networks the generalization is realized with the help of next layer neurons which fire when certain subgroups of  the lower level neurons are exited.
  This mechanism can exist in quantum mechanical networks too. But in addition to this in quantum networks there is another mechanism due to ability of quantum particle pass over all possible paths in parallel. So many quantum chains may act cooperatively resulting in generalized answer on external stimulus. Also generalized quantum states exist in such system.
 

               Quantum Lingvo Dynamics (QLD)

   SU(n) + memory matrices  =   Quantum Lingvo Dynamics

           QCD                                                            QLD
         quarks                                                         semilons
         gluons                                                          linkons
    vertex constants                                          memory matrices
       symmetry                                         symmetry broken by memory
         lattice                                                    semantic networks
 

   What's interesting that we can imagine dynamic systems which implement not
only groups (as families of elementary particles do) but also grammars.
Obviously grammar gives the rules for Feynman diagrams for such dynamic system.
  It means that together with gauge invariance and super symmetry one can use various grammars to build quantum field theory. Till now only very simple theories were used with only a few Higgs which can be considered as primitive memories.
   QLT needs two types of fields.  First type quanta are word-like,
let's call them  semilons. Second type quanta are link-like, let's call them linkons.

   Suppose that new more powerful language-like quantum field theory exists.
Than we can understand why the Word was the beginning of the All.
   The energetic word-particle of Nature language stroke another
word-particle and created all our world variety which was packed before in a vacuum.

  Quantum computations are executed by particles passing through networks. Construction of the networks is a separate complex problem - long-lived memory formation.

-----------------------------------
some other remarks:

If we have the word A, then A is really a sort of "bare word = [A]",
analogous to a bare charge in QED, plus a series of other terms that are
dependent upon the entire set of words.

A = [A] + z*sum_n([word_n]) + z^2*sum_{nm}([word_n]&[word_m]) ...

where the & word means concatenation of two "bare words" into a bare
two word combination, and z is some sort of weighting constant.  By doing this it might extend the notion of a word and a word combination into a domain that might contain more information on semantics and the like.

Let's try to imagine how the interaction of such words-particles can be organized.  First of all we need memory and a possibility to look
through this memory in parallel to see all semantic nets written.

Input set of word-particles comes, interacts with memory
and forms output set of word-particles.

Suppose one has words a(i) and set of semantic nets numbered
by index k. In every semantic net k each bond T(i,j)
connecting words a(i) and a(j) gives a term to interaction
operator V.

  V = g*sum(k) { sum(i,j) [ a(i)T(i,j,k)a(j)+ ] }

where g is a constant, a(i) and a(j)+ are annihilation and
creation operators respectively, T(i,j,k) is bond T(i,j) in net k.

When input particles come, interaction goes through creation
of intermediate virtual words-particles just like we want.

The amplitude to create output word a(j) is the sum of amplitudes over
all semantic nets.  Note that number of combinations of bonds
from different nets is huge when k grows, like situation for
NP-complete problem. But quantum mechanical system sees them all.

This is like path integral, but only the paths allowed by the memory
participate in the game.

We wrote a simple interaction operator for words without grammar .
To include a grammar one must write interaction operator according to grammar rules.

One could similarly do this with a partition function.  An interaction
term is similar to the usual harmonic oscillator Hamiltonian.  As such a
quantum interpretation would be that of a free field.  It seems that this
theory needs to be coupled to some other field, as in the case of the Dirac
field where p ----> p - ieA and where the current in the Faraday equation
is j = e(psi^*psi).   For there we would get the sort of Feynman diagrams
and analogs of radiative corrections.  It's not clear of what to
couple this system to  accomplish this.

Maybe one could imagine that each symbol has a rather large space (Hilbert
>or Banach space) assigned to it.  Each term in the series is a projection
>along one of the basis vectors in that space, something like a
>Gram-Schmidt procedure.  Then one could further imagine that the
>"concretizations" of that symbol or a whole word comes about through a
>sort of Landau-Ginzburg process that breaks the symmetry of the series and
>makes the symbol or word have some sort of definite "meaning."
 

  Memory T(i,j) itself can be a field. It plays a role of Higgs bosons, giving interaction constants for pairs of words-particles.

 First, in process of education, one forms T(i,j,k) for each semantic net k . Diagram is

   a(i) --->------\
                       |=====>== T(i,j)
   a(j) --->------/

When T(i,j) density will become significant enough, one can use the system
for recognition or generation of sentences, sending a set of input words to the system and looking at output words.

 First order diagram is

  a(i)  - --->---\
                     \ ----->-- a(j)
                      //
  T(i,j) ==>==//

In absence of input signals a(i) the wave function
of the system is given by a set of occupation numbers for fields T(i,j).
At reading a(i) come, interact with the memory, output a(j) is produced.

So then the total Hamiltonian would be

H = a(i)^{dag}a(i) + T^{ij}T_{ij}+ a(i)T_{ij}a(j)

In a sence T_{ij} would then coorespond to a machine stack.  Presumably
this stack is a function of some HO states, z_k, so that the equation of
motion would contain terms

a(i)(&T_{ij}/&z_k)a(j) & = partial.

That might work.  Maybe the Chomsky transformational grammars can be cast in this extended format.

 The question is how to proceed with such complex systems, what to begin with.

 email:  balbylon@yahoo.com            e-mail us