Elementary Synchronic model :
The "Senaire" Model
The "Senaire" Model
(for French, click on the flag)
Starting from the principle that every action is always undertaken in view of a result, or in reply to an external stimulus, we are interested in the modeling of actions with retroactive effect (feedback).
- In a first step we will start from the theory of games, to present the situation of two actors face to face.
This situation of duel, when rules of the game do not evolve, constitutes what one can define as" the present "of players.
We will call analyses that "present" with the help of a simple model: "synchronic analyses" . - In second phase, we will construct a model of several "synchronic levels" , by starting from the hypothesis that our elementary model can represent every level of an organization. We will speak, then of "diachronic analysis"
- After having used these models to drive our organization description, we can consider the former as a sort of "atomic model" able to represent any transaction type within any kind of organization.
By associating to each action energy that it puts at stake, we will apply on this well particular atom results establish by Boltzman for the theory of perfect gases.
We will propose then to characterize the global performance of an organization thanks to the measure of transaction frequencies at each hierarchical level.
![]()
Summary
- Elementary Model definition:
- Partition between desirable and undesirable:
- Uncertainty and Information:
return to "homepage"
![]()
1 / Elementary Model definition:
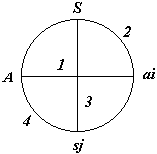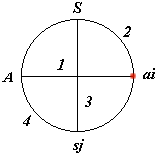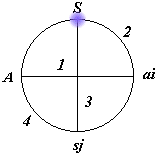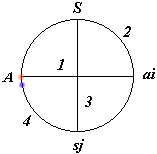
To clarify our vocabulary, we define the following terms:To define the game of the "Actor " facing the "System", we assimilate each antagonist to a player.
In any game, each player try to maximize its gain hope and to minimize its loss risk (minimax rule) .
The theory of games schematizes this face to face situation by a matrix gains and losses matrix :
| "S" losses | ||
| (s1.....si.....sn) | ||
| "A" gains |
a1 ... aj ... ap |
g11...g1i...g1n ... gj1....gji....gjn ... gp1...gpi...gpn |
Each player is represented by the totality of states on which he can be. In our example, A can take n and S p different states.
We define in extension A and S by the totality of states that they are able to take.
A = (a1,....,ap) the totality of actions retained by the Actor,
| S = (s1,....,sn) the totality of states of his relevant Environment, his target.
| |
In the precedent matrix the progress of the transaction itself is not really shown.
But we research on the contrary a model that puts directly the accent on the progress of the transaction and non on the result (the gain).
It is precisely the object of our model
When the Actor A make a chose, to global transaction between A and S, including action and reaction, can be described by the following diagram:
|
|
A and S have formally the same status, so the reply of A to a solicitation of his environment would follow the same diagram.
Thereafter, we will adopt the here above terminology:
A, S, ai & sj are called "poles" of the system.
| (A, ai) & (S, sj) are called "dipoles" of the system
| |
It is possible to use our senaire in all cases of the theory of games.
For our purpose, retain simply that the game opposing A & S can necessitate non an alone, but a series of transactions.
This series can be statistically determined, as in the case of "mixed " strategies, or destined to test reactions of the adversary, as in the case of cooperative games.
Beyond this is a possible strategy of learning by "tests and errors".
![]()
2/ Partition between the desirable and the undesirable:
When, due to a lack of information, the "Actor" can no longer define the matrix of the game, we can, in a first time, suppose that the "Actor" will try to avoid to put himself voluntarily in a state judged undesirable.
We can also suppose that, in order to avoid such situation, he has an idea of the states of the System to avoid.
In other words, we suppose our "Actor" able to realize a partition between the desirable and the undesirable.
This strategy, weaker than the "minimax" rule, is sufficient to allow us to give A & S a group structure.
Indeed, if we define an addition in A such as:
It is possible to define a neutral element "e" such as:
By definition of Å, it is impossible to choose ai or ai exclusively, so we have:
Every decision is its proper symmetrical
Proposal summarized::
We define equally Å on S such as :
![]() exclusively
exclusively
Proposal summarized::
Low strategy: :
By defining a neutral element within A and S, a strategy weaker than the minimax rule would be, for the "Actor", to make correspond "impossible decisions" of A with undesirable states of S.
We will call such transactions taboos
return
![]()
3/ Uncertainty and Information:
A develops its knowledge of S thanks to information coming from his experience thought the transactions engaged with the system.When he develops transactions with his environment, A is confronted with two types of uncertainty:
3.1/ The Actor knows the different states that S could take.
Taking the place of the actor A in our model we can try to measure his uncertainty regarding the actual state of S.When the list of states of S is defined, to look for information means to define the probability that S has to be in such or such state.
- Every state defining S has a probability more than zero (otherwise, the said state would not define S); so :
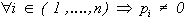
- S defined by the collection of its states is complete (from the A point of view); so :
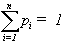
The essential point for our purpose is to note that the maximum of A uncertainty (that corresponds to a uniform probability of S state) is growing with the number of states p defining S.
One of preferential means of A to decrease his uncertainty is to "condense" or to "aggregate" the information; in other words to decrease the number of states describing "S.
(see "Stability & Information").This is the basic reason for every organization to develop a hierarchy. We will develop this idea later on.
3.2/ The Actor does not know all the states of S:
It can arrive that an action of A rests without perceptible reply from S, or reciprocally, that a stimulus of S deprives A of any possible reply and let him without reaction.There is, in this case, interruption of the cycle of transactions between A and S that one can look as a "catastrophe ".
To reply, the Actor has then to break the rules of the game, in other words to change, or modify the lists of states of A and S taken into account until this failure.
To realize this "outage" of the System, the Actor have to change his description of his interactions with the System.He has to situate himself and the System within a "meta-System".
In others words, he has to develop his strategy on two different levels, which conduct him to a diachronic" analysis..return
![]()
![]()
"System and Actor " from Crozier 1977 aux Úditions du Seuil.
This gives us the following paradox :
But, on the other hand, as part of the System taken as a whole, A
return
![]()
"Theory of games and economic behavious" of J. von Neumann & O. Morgenstern, Princeton University Press edition 1953.
return
![]()
"The absolute Structure" Raymond Abellio Editions Gallimard 1970.
Our first idea was to adapt this structure to our needs.
But, the way we use it is very far from to original author intent.
The word "senaire" was done by R. Abellio.
The term means that our model has in fact 6 poles: the 4 ones as defined here, plus 2 others which are not on the same level but connected to the upper and lower levels (we will see it in the diachronic paragraph).
return
![]()
Remark 1:
That means the Actor cannot be at the same time in two different states; and that he has to choose one - and only one - decision to respond to a stimulus of his environment.
return
![]()
Remark 2 :
e is a class gathering all the actions impossible to take, so that A has no other choose than ai.
return
![]()