Living Systems Thermodynamics

(for French, click on the flag)

After using our elementary model to describe synchronic & diachronic analysis, we can consider it as a kind of "atom " able to represent any type of transaction within any kind of organization.

If we associate to each transaction the energy involved, we can use the calculus elaborated by Boatman for the perfect gas to this very specific atom.

We would then suggest to characterize the global performance of an organization by means of a measure of the transactions occurring at each hierarchical level of it.

Until now, we defined the different possibilities of interactions between the dipoles of a senaire, without any consideration regarding the difficulty for the Actor to materialize his decisions.
We will go now under the detail of the transactions' economy, by associating to each of them the energy required.

Summary

Hypothesis:
Transaction energy:
Definition of the Synchronic Level Stable State :
1. Senaires repartition
2. Statistical temperature
Definition of Diachronic exchanges:
The senaire model as a "symbolic engine":
Effectiveness and Efficiency of an Organization:
Conclusion :

return to "homepage"

1/ Hypothesis:

Let us consider a synchronic level, on which our System is represented by a great number of senaires, acting in "parallel".
In order to conduct our calculus more easily, we will do the following hypothesis :

	*Each senaire on one level is interchangeable:* Before all, we are looking for laws governing great groups (as bureaucracies are). We are considering the case of great structures, where it is impossible to lead a great number of people by means of direct and personal contact. We call N the number of elementary senaires on the considered synchronic level .
	*On each senaire, the transactions are completed:* In other words, the two dipoles of a senaire have the same number of states, and each one commands and is enslaved to the other. This hypothesis is just to evacuate any problem regarding the accuracy of the transactions (all the actions are efficient).
	*Equi probability of senaire's states :* This is a low hypothesis, which maximizes our uncertainty. Following this hypothesis, every possible transaction has the same possibility to occur. We have no means to know in detail what is occurring within a particular senaire.

return

2/ Transaction's energy:

Let us consider an Actor A trying to act on a System S.
We suppose that no action is foreseen without any "motivation". It means that, by one way or the other, the expected profit is higher than its cost.
This implies that some "energy" is consumed by both the Actor & the System during the transaction.
In that way, we can associate an "energy" to each of the possible transactions foreseen by the Actor.
We have not to discuss now what could be this type of energy.
We have just to take into account that a measurable quantity could be linked to a transaction (as in a "gains-loses matrix").
We can note that this energy varies by step, when the senaire changes from one state to the other.

	Let *(s+1)*be the number of senaire's energy levels or the number of different values which could be taken by a senaire)
	Let wi be the value of the particular senaire's state i with *i Î (0,..., s)*
	Let gi be the number of transactions of a senaire corresponding to the energy wi,
	Let ni be the number of senaire in the energy state wi,
	Let N be the total number of senaire at the synchronic level we are discussing about.
	Let E be the global internal energy (at the synchronic level we are discussing about).

We will add the following hypothesis :

	N the number of senaire is constant (for the synchronic level considered).
	E the energy is constant (for the synchronic level considered).

Following the hypothesis defined here above, the problem to know the senaires repartition within a synchronic level is more or less the same as the problem to know the energetic repartition of the molecules within a perfect gas.
At the synchronic level we are looking at, there is no connection between senaires, each of them is isolated from the other, as well as, within a perfect gas, there is no connection between atoms. It is for that reason we develop this specific model, which can be seen as "global".
Boltzmann starts from the no connection between atoms to develop his theory.
return

3/ Definition of the Synchronic Level Stability :

The basis of Boltzman's theory is that, whatever could be our uncertainty regarding the state of a system we are describing, one thing at least is sure: this state is stable enough to allows us to see it.
So, the first thing to do it to define what is the more "stable state".
This particular state is, by definition, the one which can be reach by the greatest number of different ways.

3.1/ Senaires Repartition at the Stable State :

As a consequence of the latter hypothesis, we can now present the chain of reasoning that Boltzman developed for the first time in 1896 for the perfect gases.

The number of modes repartition P the senaires can reach is :

(refer to "Stability and Information")
The most probable repartition can be reached by the greatest possible different ways, that means for which P is maximum.

This gives us the statistical thermodynamics condition.
With our hypothesis :

	N great enough,
	N= constant,
	E = constant

we get the classical thermodynamics results : the number of senaire with the wi energy level is :

with

To simplify the following, we will take the particular case where all the gi egal 1: each transaction has the same energy.

If we consider the lower level has a zero energy we note

the number of senaires at this level.

The latter equation can be written:

The populations ni decrease very quickly, when we move away from the fundamental level

.
The shape of this decline depends of the b coefficient.

The higher is its value, the faster the decline.
b value describes, in energy terms, the more or less ability of the Actors to follow the same comportment.

3.2/ Statistical temperature:

The product

has no dimension (as an exponent of e ).
If we continue to follow the gas kinetic theory, wi is seen as a vibration energy, changing by quantum, as per the following general shape :

where n is a vibration frequency, which characterizes the kind of energy involved.

The only thing interesting for us is the possibility to characterize an energy by the means of a frequency.

We will take the following hypothesis:

For a given synchronic level, it is possible to define a transaction energy by means of a vibration measurement.

Considering now b, this coefficient characterizes the distribution of the senaires at the synchronic level we consider.

	Let be the b characterizing the j synchronic level :
	We will defined then nj as the "Transactions frequency" at the synchronic level considered j so that :

In that way, 1/ nj is a measure of the "activity" which characterizes our synchronic level.
Doing so, we give a physical sense to the common idea following which a higher degree of freedom goes with a increase of the activity level and, generally speaking with an increased level of exchanges.

return

4/ Definition of Diachronic exchanges :

Let us consider now an organization, defined by m synchronic levels.

We will consider now the exchanges between the level j and the lower level j-1:

The result of one exchange could be, for one level one or both of the following types :

The energy levels could change their values.
The populations distribution on the different energy levels could changed.

The energy variation dE resulting of this two types of fluctuation is defined as follows :

By definition :

The first term, implying a "Realisability" fluctuation is an heat exchange :
In fact, if we take into account what we said in the "diachronic analysis" paragraph, the upper level j+1 defines the game rules for the lower level j of the organization, in such a way that only two causes could push the senaire at the low level j to change their distribution :

They proper willing,
let dQj be the measure of this variation,

The information received from a lower level,
let dQj-1 be the measure of this variation.
The second term implies no variation of the whole synchronic level "Realisability" and it corresponds to a "work exchange" :
Let d Wj be the quantity of work done at the j
level (transactions rhythm increasing).

An energy variation at j level is written :

We have seen (refer to diachronic analysis) that after the level j+1defined the game rules, the level j doesn't change, until a new modification by the upper level. So we can write :

return

5/ The senaire model as a "symbolic engine":

Thermodynamics shows us that :

We can now use the former expression to show the connection between the Realisability Pe and an exchange of heat dQ.
In fact, if we take into account that b characterizes the synchronic level we consider, we have :

and

	d Ln Pj is the j level Realiability variation determined by the senaires' free will of this level.
	d Ln Pj-1 is the *j-1* level Realisability variation due to the transfer between j and *j-1* levels.

We assume that our model as well as each of its synchronic levels is in a steady state, that means that a Realisability variation at one level must be equilibrated by the summ of the variations of the other ones.
In our case, just two levels are in contact, so that we can write :

Which gives :

or :

As a senaire can take heat from the lower level, and cannot create heat at its proper level, a work is effectively done if :

This gives us a very well known result saying that a thermal engine can give a work if it takes heat from the hot source and gives heat to the cold source.

This result let us introduce an important notion we will use to measure the organization efficiency : the thermal yield.

With the hypothesis taken here, the work done at the j level is :

Let h be the yield, defined by :

, with

Let us now consider a model constructed with m synchronic levels.
To optimize the nj transactions frequencies spreading is the same as to optimize the global yield n of the whole model itself.

If we know, by experience, the highest and lowest levels frequencies, it is then easy to calculate the spread of the intermediate levels : the optimization of h implies that all the different yields are equal.
To conduct the calculus, we can take the elementary transaction time instead of the frequency :

return

6/ Effectiveness and Efficiency of an Organization:

We found a relation between the yield of an organization and the measure of transactions frequencies within the senaires. Following our latter yield definition, we can settle this rule : For a given number of synchronic levels, a hierarchical structure will be optimum when the ratio of adjacent synchronic levels transaction frequencies is constant.
. As an example, let us consider an organization with only one department where the elementary transaction average time is 5mn. (this could be the case for a bank counter). Let us suppose that the first management level receives weekly reports from this department.
We have :


	for a week of 5 working days, and 8 working hours per day.

then :

If, now, we introduce an intermediate level between two previous ones, with a 2 hours we have, then :

This result illustrates the fact that, when we make a hierarchy more flexible, by increasing the number of hierarchical levels, we reduce its yield.

In others words :

To increase the efficiency of an organization, we have to reduce the number of hierarchical levels (this is in some way the "down sizing", as practiced by management consultants),
To increase the accuracy, the effectiveness of an organization, (refer to diachronic analysis) we have to complexity its structure. As a matter of fact, it is very difficult to look for the long term development of a firm or to define a strategy, when we have to present a day to day result, or we are fighting to survive.
So, there is no "best" organization, but an optimum to find between too much and not enough hierarchical levels.
return

7/ Conclusion :

As a practical point of view :

To describe a process or an organization with senaire models is simple and gives presentation easy to submit to no-informed people.
It could be seen as just a formal presentation language.

Using always the same type of elementary model such as the senaire's one, allows us to compare organizations very different each others. In particular, we can work on systems without financial goal, such as an army or an administration, for example.

Moreover, a new field of investigation is now opened :

	Could we measure the *efficiency* and the *effectiveness* of a staff ?
	Which structure is the best one, in front of another organization ?
	What is the *yield* of an enterprise ?

Regarding the theory itself :

	We have seen a lot of connections between our theory and other ones, such as games theory, information theory, and mainly thermodynamics. This opening allows certainly a lot of theoritical developments.
	Due to the work done to formalize the living structures approach, we have made a connection between social matters and physical ones. (and that is really what we can see as a preview of *PSYCHO-HISTORY*).
	For people aware of thermodynamics theory, it could be interesting to use the "renormalization groups" to complete our theory. The main point would be to define the "*critical point*" of an organization.
	Another way, could be to consider our model as a *fractal* structure.

return

return to "homepage"

note 1 :

We cannot see a "senaire" as a physical entity, such as an individual or a group of individuals. Because our model represents only the contacts between individuals (called here "transactions").
The work of a particular individual, within a structure can be described by more than one elementary model (senaire), and can act at several different levels of the organization.

return

note 2 :

For N great enough, we define more easily the "Realisability" P, by its logarithm :

To have P maximum, the following differential has to be equal to zero :

We agregate the two conditions about N and E writing : and

If we add , member by member the two latter condition, with the arbitrary coefficients a and b we have :

At the equilibrium, this must be true, whatever could be dni, this gives the number ni of elements at the energy level wi, that means when Pe is maximum:

return

note 3 :

This hypothesis doesn't damage the the generality of our reasoning.

return

note 4 :

We can show that, if k is the most populated level, with an energy wk different than 0, the former relation takes two different expressions, depending if we consider population of upper or lower energy levels than wk.

	Upper levels:
	Lower levels:

return

note 5 :

For practical reason, we use, in thermodynamics, the so called "absolute temperature", number without dimension defined as follows : .

We prefer to use the " transactions frequency", much more adapted to our objective. Nevertheless, temperature and frequency refer to the same reality. The temperature: T is also a measure of the average gas " thermal turbulence".

return

note 6 :

Let us consider a model with an unlimited number of levels, each of them representing the same elementary senaire model. Levels differ only in the value of b.

At the optimum, as here above defined, every level can be deducted from the previous, by an homothety with a ratio of or

In other words, this model is a fractal structure with the time as fractal dimension.

return

note 7 :
We can remark that this stepping is near the optimum : indeed 1/24 is not far from 1/20. return
note 8 :
As an example, if we consider a hierarchy where the lower level transaction time is 5 mn, meanwhile the upper level transaction time is one year (of 1700 working hours), the yield versus the number of levels decreases as follows:

return

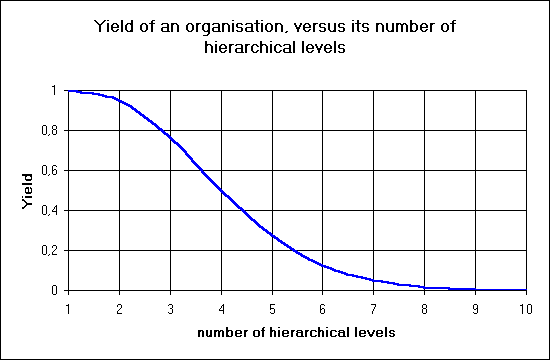
return to "home_page"

	They proper willing, let dQj* be the measure of this variation,*
	The information received from a lower level, let dQj-1* be the measure of this variation.*

	To increase the efficiency of an organization, we have to reduce the number of hierarchical levels (this is in some way the "down sizing", as practiced by management consultants),
	To increase the accuracy, the effectiveness of an organization, (refer to diachronic analysis) we have to complexity its structure. As a matter of fact, it is very difficult to look for the long term development of a firm or to define a strategy, when we have to present a day to day result, or we are fighting to survive.