Modèle synchronique élémentaire :
Le modèle sénaire

(pour la version anglaise, cliquer sur le drapeau)

Partant du principe qu'une action quelconque est toujours entreprise, soit en vue d' un résultat, soit en réponse à un stimulus extérieur, nous nous intéresserons à la modélisation des actions avec effet rétroactif (feed-back).
Dans un premier temps nous modéliserons, à partir de la théorie des jeux, la situation de deux acteurs face à face.
Cette situation de duel, lorsque les règles du jeu n' évoluent pas, constitue ce que l' on peut définir comme "le présent" des joueurs.
Nous appellerons les analyses que l' on peut faire à l' aide de ce modèle simple: "analyses synchroniques".

Sommaire

Définition d' un modèle élémentaire:
Partition entre le désirable et l' indésirable:
Incertitude et Information:

retour vers "home_page"

1/ Définition d' un modèle élémentaire:

Pour clarifier notre vocabulaire par la suite, nous nommerons:

"Acteur" (noté "A") un sujet pouvant tour à tour être observateur ou témoin, acteur dans un système ou bien "agi", ballotté par son environnement.
Le terme d' "Acteur" , présente l'avantage de mettre l' accent sur la volonté du sujet, sans pour autant préjuger du type de rapport qu'il est amené à entretenir avec son environnement: actions ou / et observations, actives ou / et passives;

"Système" (noté "S") la vision que l' acteur se fait du Monde dans lequel il évolue, sa perception forcément anthropocentrique de celui - ci.
La représentation du système est un "Modèle" créé pour les besoins d' un "Observateur" particulier. Il peut arriver que cet "Observateur" soit lui - même l' "Acteur" en question (se mettant en quelque sorte en scène).

Pour définir le jeu de l' "Acteur" face au "Système", nous assimilerons chacun des deux antagonistes à un joueur.
L' un comme l' autre tente de maximiser son espérance de gain et de minimiser son risque de perte (loi du minimax).
La théorie des jeux schématise cette situation de face à face par une matrice des gains et pertes.
La matrice suivante indique les gains de A et les pertes de S :

		*pertes de "S"*
		(s1.....si.....sn)
gains de "A"	a1 ... aj ... ap	g11...g1i...g1n ... gj1....gji....gjn ... gp1...gpi...gpn

Chacun des protagonistes est représenté par l' ensemble des états qui lui sont accessibles.
Dans notre exemple, A peut prendre p et S n états différents.

Nous définirons en extension A et S par l' ensemble des états qu' ils sont susceptibles de prendre.

	A = (a₁,....,a_p) l'ensemble des actions retenues par l' Acteur,
	S = (s₁,....,s_n) l'ensemble des états de son Environnement pertinent, sa cible.

Le gain g_ji n' est acquis qu' après réalisation de l' action d 'un joueur et la réaction consécutive du joueur antagoniste, ensemble que nous appellerons "transaction".
Dans la représentation matricielle précédente, le déroulement de la transaction proprement dite est escamoté.
Or, nous recherchons au contraire un modèle qui mette directement l' accent sur le déroulement de la transaction et non sur le gain proprement dit.
C' est précisément l' objet de notre modèle : L' acte de jouer peut se ramener, lorsque A fait un choix ai au schéma suivant:

Choix de A : A ==> ai
Action de A : ai ==> S
Choix de S : S ==> sj
Réaction de S: sj ==> A

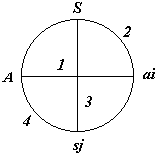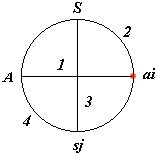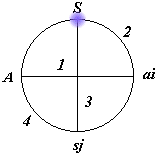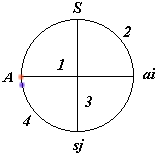A et S ayant formellement le même statut, la réponse de A à une sollicitation de S suivrait le même schéma.
Par la suite, nous adopterons la terminologie suivante:

	*A, S, a_i* & s_j seront appelés les "*pôles*" du système.
	*(A, a_i)* & (S, s_j) seront appelés "*dipôles*" du système

Le modèle lui-même, mettant en relation les deux dipôles précédents sera appelé "sénaire" .
On peut montrer qu' il est possible d' utiliser notre sénaire dans tous les cas de la théorie des jeux.
Pour notre propos, retenons simplement que le jeu opposant A & S peut nécessiter non pas une seule, mais une série de transactions. Cette série peut être statistiquement déterminée, comme dans le cas des stratégies "mixtes", ou destinée à tester les réactions de l' adversaire, comme dans le cas des jeux coopératifs.
Entre alors dans le modèle une notion d' apprentissage par "essais et erreurs".
retour

2/ Partition entre le désirable et l' indésirable:

Lorsque, faute d' information, l' Acteur ne peut plus définir la matrice du jeu qui le lie au Système, nous pouvons, dans un premier temps, supposer qu' il cherche à éviter de se mettre volontairement dans un état jugé indésirable et peut se représenter les états du Système qu'il veut éviter.
Autrement dit, nous supposons notre acteur capable de réaliser une partition entre le désirable et l' indésirable.
Cette stratégie, plus faible que celle du minimax, est suffisante pour nous permettre de doter A & S d' une structure de groupe.

En effet, si nous définissons une addition dans A telle que :

exclusivement
il est possible de définir un élément neutre "e" tel que :

Comme par définition de Å, il est impossible de choisir a_i ou a_i exclusivement on a :

Toute décision est donc son propre symétrique.
Proposition résumée:

est un groupe commutatif.

On définit également Åsur S tel que :

exclusivement
Proposition résumée:

est un groupe commutatif.

Stratégie faible :
En définissant un élément neutre dans A et S, une stratégie plus faible que celle du minimax serait, pour l' Acteur, de faire correspondre les décisions impossibles de A aux états indésirables de S.

Nous appellerons de telles transactions des "tabous".

retour

3/ Incertitude et Information:

A développe sa connaissance de S grâce aux informations qu' il retire de son expérience.
Au fil des transactions qu' il développe, l' acteur est confronté à deux types d 'incertitude:

3.1/ L' Acteur connaît les différents états que S est susceptible de prendre.

Prenons la place de l' acteur A dans notre modèle et cherchons à mesurer son incertitude concernant l'état de S.
La liste des états de l' ensemble S étant définie, rechercher de l' information signifie définir la probabilité qu' a S de se trouver dans tel ou tel état.

Chaque état est affecté d'une probabilité supérieure à zéro, faute de quoi l'état en question ne serait pas un élément de S. Donc :
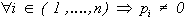
La description de S par la collection de ses états est complète aux yeux de l' acteur, aussi :

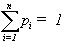
Notre incertitude concernant l'état effectif de l'ensemble S, peut alors être définie par

Le point essentiel pour notre propos est de noter que l' incertitude maximum de l' Acteur (qui correspond à une probabilité uniforme des états si ) est une fonction croissante du nombre d' états p de S.
L'un des moyens privilégié de A pour diminuer son incertitude est de "condenser" ou d' "agréger" l' information; c' est à dire diminuer le nombre d' états de S envisagé (voir note sur la information & stabilité).

3.2/ L' Acteur ne connaît pas tous les états de S:

Il peut arriver qu 'une action de A reste sans réponse perceptible de S, ou réciproquement, qu' un stimulus de S prenne A au dépourvu et le laisse sans réaction.
Il y a, dans ce cas, interruption du cycle des transactions entre A et S que l' on peut regarder comme une "catastrophe" .
Pour répondre, l' Acteur doit alors sortir du jeu, c' est à dire changer, modifier les listes d' états de A et de S prises en compte jusqu' à cet échec.

Pour réaliser cette "sortie" du système, il faut déclencher une action destinée à modifier le système lui-même, se situer dans un "méta-système".
Cette prise en compte de différents niveaux d'intervention nous conduit à une analyse "diachronique" du système étudié.

retour