Квантование скоростей в СТО.

СТО не является квантовой теорией. В настоящей работе предполагается, что скорость, с которой может двигаться элементарная частица, не может иметь непрерывный ряд значений. Скорость может меняться малыми порциями. Элементарная частица, имеющая массу покоя, не может иметь ни нулевую скорость, ни скорость, равную скорости света. Макроскопический объект может иметь скорость равную нулю, поскольку он состоит из множества элементарных частиц. Пускай для наглядности он состоит из двух элементарных частиц. Тогда если одна из частиц движется в одном направлении с минимально возможной скоростью, а другая - в другом направлении с такой же скоростью, то скорость этого составного тела будет равной нулю.

Кроме того, в этой работе предполагается, что элементарная частица сама по себе является составной. По всей вероятности, она имеет от одного до четырёх элементов, которые мы будем далее называть звеньями пространственно-временной решетки. Дефекты пространственно-временной решетки вращаются по почти замкнутым окружностям, спиралям со скоростью c и "сталкиваются" в некоторых точках, лежащих на мировой линии элементарной частицы. Шаг спирали говорит нам о скорости частицы v. Моменты "столкновения" дефектов решетки являются актами материализации элементарной частицы. Элементарная частица не существует в моменты времени между микро-материализациями, или для частицы не существует времени между микро-материализациями. Кроме микроскопических синхронизаций (слабая, сильная, электромагнитная) существует также макроскопическая синхронизация, происходящая с частотой порядка 734 Гц, и добавляющая этим частицам еще одно звено - гравитационное.

От описания поведения элементарных частиц в пространстве-времени можно перейти к описанию структуры пространства-времени. Как его структурировать? Вероятно, для каждого типа элементарных частиц эта структура выглядит несколько по-разному. Нестабильные частицы плохо вписываются в эту структуру, и распадаются на стабильные. Стабильными элементарными частицами являются протон, электрон и их античастицы.

С учетом вида взаимодействия можно рассматривать отдельные "сечения" структуры пространства-времени. А полученные результаты можно попытаться перенести на другие сечения.

Сравнивая электромагнитные взаимодействия с гравитационными, мы получаем классический радиус частицы. Действительно, мы получаем его, приравнивая энергию покоя частицы (E = mc², где: m - инертность, являющаяся характеристикой гравитационных взаимодействий) и энергию электрического поля, полагая, что вся масса частицы сосредоточена в форме поля, (а поле есть характеристика электромагнитных взаимодействий). На сравнении этих взаимодействий мы также получили некоторые соотношения, и, прежде всего, большое квантовое число N.

На классический радиус мы также можем выйти, исследуя симметрию между зарядом и массой на микроуровне. Это мы делаем, полагая, что масса частицы есть мера инертности при её ускорении в пространстве, а заряд есть мера инертности при его ускорении во времени.

С другой стороны, используя формулу mc²=hc/(2pr), мы получим комптоновский радиус, который в 1/a раз больше классического. По предположению в этой работе, комптоновский радиус определяет расстояния, на которых могут находиться одновременные параллельные линии; а на классическом радиусе мы можем работать абсолютно точно относительно некоторой точки, но неопределенность положения этой точки в пространстве и времени определяется комптоновским радиусом.

О фундаментальности классического радиуса здесь сказано в связи с тем, что именно через этот радиус удалось выйти на квантуемую скорость. А используя связи между разными видами скоростей, мы можем найти полные наборы допустимых скоростей.

В настоящей работе показаны следующие виды скоростей: координатная скорость v=dx/dt, собственная скорость v_t=dx/dt, быстрота v_y=c·Arth(v/c), квантуемая скорость v_q=c·Arcsin(v/c).

На странице Квантуемая скорость и Модель элементарной частицы показаны некоторые свойства квантуемой скорости.

Главное свойство квантуемой скорости заключается том, что если элементарный заряд падает на противоположный заряд, закрепленный в точке с координатами (x=0, ict=0=const), то его образ монотонно пробегает все точки правой и левой гиперболы. При делении каждого элемента гипербол на релятивистский коэффициент (chy = g) две гиперболы превращаются в окружность радиуса r_cl. При этом образ частицы движется по этой окружности равномерно. Длина дуги, измеренная от точки пересечения с осью x до нижней точки окружности, есть величина -r·ip/2, а до верхней точки r·ip/2. Разделив эти значения на r·i, мы получим фазу колебаний Q, и она же есть параметр квантуемой скорости, Q. Умножая этот параметр на скорость света, получаем квантуемую скорость v_q=c·Q.

Действительно, длину четверти окружности дает нам половина гиперболы при делении каждого её элемента на релятивистский коэффициент chy, и последующего взятия интеграла с пределами интегрирования от нуля до плюс бесконечности.

Q_(1/4) = _oI^+оо dy / chy = p/2

Разделив окружность на 2N равных дуг, мы можем получить полный набор значений квантуемой скорости. Зная этот набор, мы можем получить наборы других типов скорости (координатной v_t, собственной v_t, быстроты v_y). Число N это большое квантовое число. В настоящей работе оно предполагается равным 3,09·10²⁰. Происхождение числа 2 объясняется тем, что для того, чтобы перейти от скорости v_q=-pc/2 до скорости v_q=+pc/2, нам нужно пройти не полную окружность, а лишь половину окружности, или одну полную гиперболу. В пачку ИСО (см. раздел Квантовая Гравитация) входит 2N ИСО. N ИСО движутся вправо, и N ИСО движутся влево.

Кроме того, необходимо учесть, что, превращая окружность в многоугольник, мы должны учесть, что значение минимальной скорости не должно быть равно нулю, а значение максимальной скорости не должно быть равно в точности "с". Этого мы можем добиться, строя правильный 2N-угольник так, чтобы оси x и ict пересекались срединами ребер получаемого 2N-угольника.

Тогда минимальное значение параметра квантуемой скорости будет определяться интегралом

Q_min = Q₁ = _oI^y1 dy / chy = (p/2) / N = p / 2N.

Следующее значение параметра квантуемой скорости отстоит на целое ребро 2N-угольника, то есть, на p/N больше за первое значение.

Q₂ = _oI^y2 dy / chy = p / 2N + p / N = 3p / 2N.

Следующее допустимое значение:

Q₃ = _oI^y3 dy / chy = p / 2N + 2·p / N = 5p / 2N.

Очевидно, что n-e допустимое значение параметра квантуемой скорости будет определяться по формуле:

Q_n = _oI^yn dy / chy = p / 2N + (n-1)·p / N = (2n-1)·p / 2N.

Максимальное значение параметра квантуемой скорости будет при n=N/2:

Q_max = (N -1)·p / (2N) = p / 2 - p / 2N.

Перейдем от параметра квантуемой скорости к параметру быстроты, пользуясь соотношением tg(Q/2)= th(y/2).

y_n = 2Arth(tg(Q_n/2)) = ln((1+tg(Q_n/2))/(1-tg(Q_n/2))) = ln(tg(p/4 + Q_n/2))

y_min = p / 2N,

y_max = ln(4N/p).

Запишем выражения для допустимых значений координатной скорости, пользуясь соотношением v=c·sinQ.

v_n = c·sinQ_n= c·sin((2n-1)·p / 2N).

v_min = c·p / 2N.

v_max /c = sinQ_max = sin(p / 2 - p / 2N) = cos(p / 2N) =
= (1- (sin(p / 2N))²) ^1/2 = (1- (p / 2N)²) ^1/2 =
= 1 - p² / 8N².

Запишем выражения для допустимых значений собственной скорости, пользуясь соотношением v_t=c·tgQ.

v_t,n = c·tgQ_n = c·tg((2n-1)·p / 2N).

v_t,min = c·tg(p / 2N) = c·p / 2N.

v_t,max /c = shy_max = sh(ln(4N/p)), Arsh(v_t,max /c) = ln(4N/p),
ln(v_t,max /c + ((v_t,max /c)² +1)^1/2) = ln(4N/p)
v_t,max/c = 2N/p.

Запишем выражения для допустимых значений релятивистского коэффициента g, пользуясь соотношением g = 1/cosQ = chy.

g_n = 1/cosQ_n = 1/cos((2n-1)·p / N).

g_min = 1/cosQ_min = 1/cos(p / 2N) = 1 / (1 - p² / 8N²) = 1 + p² / 8N².

g_max = 1/cosQ_max = 1/cos(p/2 - p / 2N) = 1/sin(p / 2N) = 2N/p.

Итак, максимальное значение релятивистского коэффициента g_max равно 2N/p. О чем это говорит. Каким станет классический радиус электрона, если он будет двигаться с максимально возможной скоростью? Для ответа на этот вопрос разделим r_cl = e² / (4pe₀mc²) на 2N/p. Величина N используется повсеместно в нашей работе, и N = (ap / df)^1/2, где df есть отношение сил для электрона, df=4pe₀Gm²/e².

r_cl' = r_cl / (2N/p),

r_cl' = (e² / (4pe₀mc²)) / (2(ap / df)^1/2/p),

r_cl' = (hG / 8c³)^1/2.

Полученная величина с точностью до коэффициента равна планковской длине, которую обычно записывают в виде

r_Pl = (hG / 2pc³)^1/2.

Можно сказать, что мы ошиблись на числовой коэффициент. Но планковские величины никто никогда не наблюдал. Это лишь простой набор констант, дающий естественную длину на микроуровне. Поэтому, полученная нами формула не менее верна.

Аналогично можно показать, что релятивистская масса электрона, движущегося с максимально возможной скоростью, равна "нашей" планковской массе:

m_r = m₀ · 2N/p.

m_r = (a/p)·(2hc / G)^1/2.

Обычно планковскую массу записывают в форме:

m_Pl = (hc / 2pG)^1/2.

Здесь мы тоже получаем отличие от общепринятой формулы в численный коэффициент. Не исключено, что в полученные нами формулы должно входить некоторое другое большое квантовое число, тем более, что наша N получена, прежде всего, через космологические параметры и параметры протона. Аналогичные рассуждения, с получением классического радиуса, и описанием движения по гиперболам, можно было бы провести и для самого протона, но, к настоящему времени у меня сложилось впечатление, что "сильное" звено протона вращается в плоскости (y,z), а его электромагнитное звено (позитрон) вращается в плоскости (x,ict), точно также, как и для электрона, но в противоположную сторону. Логично предположить, что "сильное" звено вращается по окружности в m_pr/m_el раз меньше чем электромагнитное. Это как раз то колечко, сквозь которое пролетает электрон в своем колебательном движении вдоль оси x.

Возвращаясь к полученному результату (g_max=2N/p), можно заметить еще одну деталь. Если длина большой окружности Вселенной определяется по формуле X = Nl₀ = N²l_pr, где l₀-граничная длина волны между фотоном и гравитоном, l_pr - комптоновская длина волны протона, то Вселенная относительно электрона, движущегося с максимально возможной скоростью, будет сокращена в 2N/p раз. Разделив X=Nl₀ на g_max=2N/p, мы получим l₀·p/2. А это и есть длина "гравитационного звена", которое частицы пролетает её за время

t = (l₀·p/2) / v_q.max = (l₀·p/2) / v_q.max = (l₀·p/2) / (cQ_max) = l₀/c = t₀.

Величина t₀ есть граничный период между электромагнитными и гравитационными колебаниями, то есть между гравитонами и фотонами. Величины N, l₀, X, ... и многие другие смотри на Excel-странице.

Главный вывод. Исследование квантованной скорости даёт нам новую возможность к построению моделей элементарных частиц. В следующем разделе понятие квантованная скорость разобрано более детально. А в конце даётся примерная схема моделирования элементарных частиц.

Вперёд: Квантуемая скорость и Модели элементарных частиц.

Назад: Разные формы записи преобразования координат.

К оглавлению раздела Некоторые вопросы СТО.

К другим разделам Космической Генетики.

29 мая 2007 года.

Иван Горелик

Моё резюме

20 марта 2009.

О возможных уточнениях на будущее.

Идея представления элементарных частиц в виде пересекающихся квазизамкнутых окружностей пришла давно, - в конце девяностых. Квантованную скорость я поучил в 2007-ом году. Она очень удачно согласуется со старой идеей и обогащает её. Но есть пока не до конца понятные вопросы. Где должен находится горизонт событий? Если так:

21 марта 2009.

Проблема с коэффициентом p/2, который мы получили при непопадании на планковские и граничные величины вероятно может быть решена, если мы будем применять два главных квантовых числа N и N*=Np/2. Минимальную координатную скорость мы получаем при делении с на N. Минимальную квантуемую (тригонометрическую) скорость мы получаем при делении cp/2 на N*. При этом мы получим одно и то же число.

А как быть с рисунком выше. Его по-видимому придется уточнить.  При медленном обходе Вселенной мы получаем число N, то есть X=λ₀N. Но в количество линий в пачке, движущихся в одном направлении, должно быть Np/2. Столько же в противоположном. Это полсферы Вселенной. А вторая половина Вселенной - наше зеркальное отображение. Мы находимся на двух противоположных полюсах одновременно...

Внести поправку в Библию Времени. Каждая последующая секунда длиннее предыдущей, но не в одно и то же число раз, а в соответствии с законом, связующим координатную скорость и квантуемую. То есть, нужно записать закон описывающий "вес" минимальной квантуемой угловой дуги dQ=p/2/N* в зависимости от того, на каком расстоянии она находится от начала, где Q=0. 

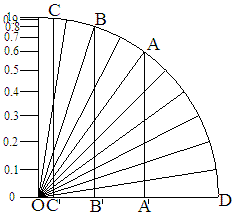
Задача. По реке плывет плот со скоростью v₁=0,8с. На рисунке этой скорости соответствует отрезок BB'. Этот плот имеет квантуемую скорость обозначенной дугой DB, которая будет равна v_q1=0,9273с. По плоту в том же направлении бежит собака с координатной скоростью v₂=0,6c относительно плота. Этой скорости соответствует отрезок AA', а соответствующая квантуемая скорость обозначена дугой DA и она оказывается равной v_q2=0,6435с. Если мы возьмем отношения соответствующих скоростей то получим  v₁/v₂=1,3333; v_q1/v_q2=1,4410.

Вопрос: Что движется быстрее и во сколько раз, плот относительно берега, или  собака относительно плота?

Ответ: Поскольку в вопросе присутствует слово "быстрее", то мы должны найти соответствующие быстроты и сравнить их. Оказывается: v_ψ1=1,0986; v_ψ2=0,6931; v_ψ1/v_ψ2=1,5850. Плот быстрее собаки в 1,5850 раз. Это отношение не равно отношениям приведенным выше.

Если мы возьмем отношение собственных скоростей, а это есть "отношение показаний спидометров", то получим: v_b1=1,3333; v_b2=0,75; v_b1/v_b2=1,7778. Итак, четыре разные типа скорости, дают четыре разных отношения. Эти отношения становятся равными друг другу в одном случае, когда скорость собаки относительно плота равна скорости плота относительно берега. При этом все отношения дают единицу.

22 марта 2009.

На верхнем рисунке показано деление окружности на равные сектора. На нижнем рисунке показан набор скоростей, который мы получим, если возьмем какую-то минимальную скорость v₁=dv и далее находим v_i в соответствии с законами сложения скоростей. Несмотря на то что эти законы для разных типов скоростей выглядят по разному, картинка получается одинаковой для любого вида скоростей с соответствующим законом сложения.

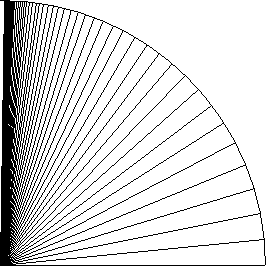
При построении этого рисунка были взяты следующие данные:  c=1; dv=1/200. Сложено 1000 одинаковых скоростей. Нарисована каждая 20 линия.

Законы сложения i одинаковых скоростей:
v_i = th(i Arth(dv));
v_bi = sh(i Arsh(dv));
v_ψi = i dv.
Связующие формулы:
v = sin(v_q);
v_b = tg(v_q);
v = th(v_y);
v_b= sh(v_y);
th(v_y/2) = tg(v_q/2).
Красивого закона сложения для квантуемой скорости пока не получено, но  для неё получен тот же график, используя дополнительные преобразования.