Параметр быстроты y, быстрота r.

Координатная и собственная скорости не являются аддитивными. Было замечено, что закон сложения координатных скоростей напоминают запись гиперболического тангенса от суммы двух углов. Это будет заметнее, если мы разделим обе стороны уравнения на с:

v = (v₁+v₂) / (1 + v₁v₂/c²),
v/c = (v₁/c+v₂/c) / (1 + (v₁/c)(v₂/c)),
thy = th(y₁+y₂) = (thy₁+thy₂) / (1+thy₁thy₂).

Угол, в отличие от тангенса угла, - величина аддитивная. Поэтому в специальной теории относительности были введены безразмерный параметр быстроты y и быстрота r, размерность которой совпадает с размерностью скорости.

y=y₁+y₂;
r=r₁+r₂;
r = y c.

Координатная скорость и коэффициент гамма могут быть выражены через гиперболические функции от этих величин. Оказалось, что собственная скорость дополняет данную группу равенств

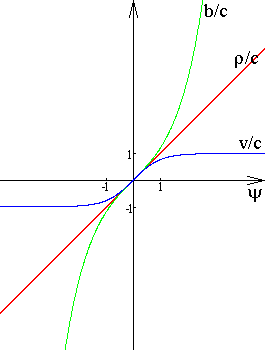
v/c = thy = th(r/c);
g = chy = ch(r/c);
b/c = shy = sh(r/c).

На рисунке ниже показаны графики b/c=shy, v/c=thy, r/c=y.

Параметр быстроты и быстроту можно получить по формулам

y = r/c = Arth(v/c) = (1/2)ln((1+v/c)/(1-v/c)),
y = r/c = Arsh(b/c) = ln(b/c + g) = ln(b/c + sqr(1+b²/c²)),
y = r/c = Arch(sqr(1+b²/c²))=Arch(g).

Закон сложения для множества одинаковых координатных скоростей v₀ может быть записан в виде

v/c = thy = th(ny₀) = th(nArth(v₀/c)).

Или для множества v_i, параллельных между собой, но разных по абсолютному значению:

v/c = th(Arth(v₁/c)+Arth(v₂/c)+Arth(v₃/c)+...),

Закон сложения собственных скоростей напоминает выражения для синуса гиперболического от суммы двух углов:

b = b₁g₂+b₂g₁,
shy = sh(y₁+y₂) = shy₁chy₂+shy₂chy₁.

Для множества одинаковых собственных скоростей b₀ получим:

b/c=shy=sh(ny₀)=sh(nArsh(b₀/c)).

Или для множества b_i, параллельных между собой, но разных по абсолютному значению:

b/c=sh(Arsh(b₁/c)+Arsh(b₂/c)+Arsh(b₃/c)+...).

Эти величины можно выразить через экспоненты:

v/c = thy = (e^y-e^-y)/(e^y+e^-y),

b/c = shy = (e^y-e^-y)/2,

g = chy = (e^y+e^-y)/2.

Пользуясь соотношением ch²y - sh²y = 1, проверим справедливость формулы g=sqr(1+b²/c²):

g² - b²/c² = (1+b²/c²) - b²/c² = 1.

Дальше: Интервал.
Назад: Два вида измеримых скоростей в СТО.
К оглавлению раздела Некоторые вопросы СТО.
К другим разделам Космической Генетики.

Иван Горелик

Моё резюме