Practical Overunity Energy Devices

Introduction

Recently, my associates and I have filed a patent application on what we believe will at long last reveal the mechanisms for practical overunity electrical devices. It is my purpose in this paper to provide additional information augmenting my former two papers, (1) "The Final Secret of Free Energy," Feb. 1993, and (2) "Additional Information on the Final Secret of Free Energy," Feb. 1994. In this present paper, with the permission of my colleagues, I release the gist of our work on separation of electrical charge into two coupled components ()(m), where represents the massless charge of the charged particle or mass, represents the fact that it is coupled or trying to couple to the special mass that makes up charged particles [i.e., the special kind of mass that will couple to the virtual photon flux density that is represented by the symbol ], and m represents the inert mass component of the charged mass. Since not all masses will couple with , we indicate the type of mass that will couple with it, as m. Thus a charged mass is composed of ()(m), which we consolidate to ()(m).

Charge Is Not Quantized

An interesting immediate result is that the massless charge of a fundamental charged particle is not quantized; it changes as a function of the background potential in which it is embedded. So it is discretized as a function of the background potential (i.e., of the virtual photon flux exchange between it and the surrounding vacuum). Otherwise, e.g., there could be no created on any charged particle q, and hence no E-field, and hence electrons would not move in our present circuits. Since they do move in our circuits, charge is not quantized.

Electrical Current Has Two Components

The first key to understanding free energy electrical and magnetic machines is to realize that electrical current actually consists of two currents coupled together. Our treatment of an electric charge as a coupled system ()(m) also means that electron current i = dq/dt is comprised of two coupled components [(d/dt)(dm/dt)]. This follows from simply invoking the operator d/dt; i.e., d/dt[()(m)] = (d/dt)(dm/dt), which is the same as [(d/dt)(dm/dt)]. The component (d/dt) is the known but not well understood massless displacement current, while the component (dm/dt) is the mass displacement current, and the coupling operator means "coupled to" or "trying to couple to". The coupling operator represents a real physical operation: the exchange of virtual photons between the vacuum potential and the charged mass. Any potential ₁ is considered to be a potential that is superposed upon the ambient vacuum potential ₀, to provide a potential (₀+₁). The ambient vacuum potential does not disappear merely because we add another potential to it!

Confusion In Present Electrical Physics

We point out that, in physics books of note, the overt coupling effect is essentially unknown or ignored because physics presently has not defined either the scalar potential or the electrical charge. The conventional theory simply uses an "inert" expression d/dt to represent the displacement current (and another inert expression q for a charged mass), and most theoreticians are uncomfortable even with that. The displacement current is also confused with force by equating the displacement current d/dt to dE/dt. In turn, this means that d/dt is confused with mass, hence with dm/dt, which latter is also a component of dq/dt. m is always an internal component of force, as is known in foundations of physics but this fact continues to remain completely oblivious to the electricians. [Good electrical theorists do admit that there is no force in the vacuum; and that the force associated with the E-field is evidenced only in the interacting mass. However, they continue to maintain the E-field (force per point-coulomb of charged mass) in the vacuum, when there are no point-coulombs of charged mass there!

Mass Is an Internal Component of Force

It is easy to show that mass is always a component of force: We will simply define force precisely. We first insist that no equation can be used as a definition; an equation simply states that the magnitude of one of its sides and the magnitude of the other side are equal. (The length of a board and the length of a human may be equal, but writing that as an equation has absolutely nothing to do with the definition of either a board or a human). So we will insist that any true definition must be an identity.

We define force F as F d/dt(mv), whereupon mass is a component of force a priori. It follows that, if we define the E-field E as the force per coulomb, we are defining it as the force existing at a point and having a point-coulomb of charged mass as one of its major components. We may accurately now define E as E -[()(q)]/|q|, where the absolute value symbol in the denominator is essential, q/|q| being one point-coulomb. [We leave as an exercise for the reader the further reduction of this definition by treating q as (m)].

At any rate, with the new and correct definition of the E-field, one can see that the flow of displacement current (d/dt) upon a collector such as a rigid capacitor, containing a fixed charge (m), will result in the formation of an excess upon those restrained charges in the capacitor plate, so that there is created an E -[()(q)]/|q|. Since the conventional theory considers the antigradient of the potential as an E-field, then one can now see the exact mechanism that creates this E-field that grows upon the capacitor (across its plates) as it charges. In fact, the q/|q| cannot change in a capacitor if its plates and dielectric are immovable. Instead, in that case, the portion of the trapped (q) changes, producing the () change. Since the () component is coupled to the mass component of the fixed q as (+)m, then an E-field is created and exists as E -[()(q)]/|q|.

An Ideal Capacitor Is an Electron Current Blocker

We point out that, if the capacitor's components are ideal, completely rigid, and do not physically move, then the capacitor is a "dm/dt blocker." If the charges really were frozen in place, then the potential would flow across the plates at the speed of light, via the flow of excess massless displacement current d/dt. In that case, an ammeter would not show the classical "exponential fall-off" of the current with time; the electron current dq/dt would occur as a single-point Dirac delta function at t=0, and would be zero thereafter. And no electrons would be able to move in zero time. The voltage would show an instantaneous adjustment to the charged value with a single step-function, and the capacitor would charge up fully, instantly, with no work (energy loss) whatsoever being done. And this charge-up of the capacitor would not dissipate in the slightest the source furnishing the voltage; there would be no electron current dq/dt through the back EMF of the source, hence no work inside it to deplete its separation of charges.

Problems With Ordinary Capacitors

However, most ordinary capacitors are much more than just an ideal capacitor. The plates move, the dielectric moves, etc. due to the forces created upon them by the E-fields created upon the trapped charges in them. The spatial translation of the resulting force moving the plates constitutes work; i.e., it dissipates some of the flowing d/dt energy. Each movement of the plates and/or dielectric carries with it all its internally trapped charges. The movement of those charges constitutes a substantial longitudinal electron current dq/dt, when compared to the longitudinal "drift" electron current in normal circuits. [Electrons spend most of their time moving radially in a wire, not down it.] This "moving plate and its transported charges" make an electron current, which pumps the inert electrons in the ground return line back through the back EMF of the source, depleting the source. Consequently, the ordinary capacitor will simply release as much energy as work (to move the plates and dielectric) as it stored. Hence, it will also produce dissipation of the source via the amount of energy stored in the capacitor. You still get "free energy" stored in the capacitor, but also dissipate the source by an equal amount.

Rigidized Capacitors Must Be Used

Only rigidized capacitive collectors are useful in free energy devices. Such capacitors are in fact actually available, e.g., as calibration standards, but they are extremely expensive ($400 to $2,000 or so each, for a capacitance reaching about 1 F).

So, capacitive type collectors must be rigidized, if used in overunity circuitry. Even so, in a single integrated circuit, although one collects free energy, one will use half of what was collected to dissipate the source. Not all the remaining half will be discharged through the load; some will be discharged in other circuit and component losses. Hence, there will always be less work done in the load than is done in the source to kill it, by a conventional two wire single closed circuit. In my second referenced paper (Feb.94), I included precise proof that this is true. One must use energy collection and shuttling between two isolated circuits, and the load discharge current must not pass back through the primary source of potential.

We have previously provided precisely how to utilize capacitive collectors in our two referenced papers. We point out here that the capacitors must be calibration standard capacitors, or specially made rigidized capacitors.

It Does Not Require Electron Current to Charge An Ideal Capacitor

For the benefit of the skeptic, this is already proven. We simply list references (2) and point out the equation that represents the energy K in a charged capacitor. Here we have K = 1/2(CV)². It is totally the displacement current d/dt flowing (from a higher potential) onto the charging plate that produces the higher potential on that charging plate, and hence a V between the two plates, one of them (the "ground" side) being held at a constant potential. The mass displacement current component dm/dt of the electron current dq/dt has nothing whatsoever to do with energy accumulation; it has only to do with the dissipation of energy that is happening simultaneously in all losses and loads in the circuit loop.

We reiterate that most ordinary capacitors have terrible internal movement, and accomplish as much energy dissipation as they do energy collection by permitting dq/dt and work performed upon the plates and dielectric to move them. The standard two-wire circuit also guarantees that all such dq/dt current "through" the capacitor is passed back through the source against its back EMF, doing an equal amount of work in the source to dissipate its separation of charges and "destroy" the source.

An ideal capacitor does not pass dq/dt, but only massless displacement current as theorized by Maxwell to save current continuity in a circuit containing a capacitor, and hence to save Ampere's current law. That is, an ideal capacitor is a dm/dt blocking device. However, the capacitors utilized in normal circuits are not ideal capacitors at all. By allowing the plates to move, electron current dq/dt is created on both sides of the capacitor. Otherwise there would not be a ground return dq/dt, but only a ground return d/dt. This d/dt would not and does not push electrons back up through the source against its back EMF; else the ground side of the source, which is engaged in continuous d/dt exchanges with the vacuum, would produce destructive amperage d/dt in the battery or potentialized source, against its back EMF, while it was simply sitting on the shelf. In fact, a flow of d/dt continually runs from the vacuum to the positive terminal, then through the inside of the battery to the negative terminal, and thence back to the surrounding vacuum. Also, the incoming flow from the vacuum "splits" at the positive terminal, where one branch flows inside the source to the negative terminal, and the other branch flows through the external circuit to the ground return line, and thence to negative terminal and back to the vacuum. In the external circuit, the d/dt hooks to free electrons and moves them as ordinary dq/dt. In the internal circuit inside the source, the electrons are restrained, hence they only move when their restraint is overcome.

Displacement Current d/dt Is Real

In recent years, SQUID detectors have been utilized to detect the magnetic field created between the plates (at right angles) by the displacement current d/dt between the plates, providing strong evidence that displacement current is physically real. The best proof that it is real is a charge blocking device, two isolated circuits using energy collection and shuttling, and overunity powering of loads in the secondary circuit.

A Problem With Ammeters and Measurement of d/dt

Note that an ammeter cannot differentiate between displacement current d/dt and normal current dq/dt. In the ammeter, the sample d/dt will couple to free electrons, producing a normal dq/dt inside the ammeter. The driving of this dq/dt through a precision resistance, e.g., is measured and the instrument is calibrated to show the dq/dt amperes flowing. One of the major needs of free energy researchers is the development of a good current meter that will differentiate between d/dt and dq/dt, and measure each one. Short of using a mass spectrometer to differentiate the mass current dm/dt, and comparison of those mass current measurements with an ammeter's measurements of the "current" dq/dt, and calculating the d/dt from that, I presently know of no way to precisely and simply measure and separate the two current components. I have been thinking of utilizing a multi-channel sampling meter set arrangement, where one channel uses a dm/dt blocking device such as the Fogal semiconductor in this respect, but have not yet developed the complete concept.

Better Solution: A Charge Blocking Device

A better solution than the capacitor or capacitive collector is the use of a special rigid solid state "charge blocking device", such as a Fogal semiconductor, to enable the current separation into two components, blocking of the mass flow component, and passage of the massless displacement current component. In overunity electrical devices, it is massless displacement current d/dt that must be separately passed down the primary circuit and collected in the collector as an E-field or an H-field. This provides "free" energy that has been extracted from the vacuum, via the potential difference between the terminals of the source antenna, and collected and stored in the appropriate field, without work. The collected free energy may then be transferred to the isolated load circuit by a variety of means, for separate discharge through the load without return of dq/dt through the source.

The Fogal Semiconductor Meets the Charge-Blocking Requirements

Fogal's marvelous semiconductor blocks passage of electrons into its output terminal, but passes displacement current d/dt into it. The semiconductor is powered by (receives) normal electron current and excess d/dt, but outputs pure massless displacement current d/dt. A charge blocker that passes d/dt is ideal for our overunity mechanisms, enabling them to be readily obtained as we shall shortly see.

Energy, Flow, Finite Amount of Energy, and Collectors

We accent that the flow of energy in an electrical circuit is purely by means of the massless displacement current component (d/dt). The flow of the mass component (dm/dt) represents the "flow of work" (energy dissipation) in the circuit. Power is rigorously the time rate of doing work, and electron current dq/dt is a part of power. It has nothing whatsoever to do with the time rate at which energy is transported without loss; instead, power represents the rate at which energy "leaks" or is "lost" during its transport.

All measurement is work, not energy. Energy cannot be measured, even in theory, a priori. Energy is also a flow process, and never a finite amount in one location. A specific differential of energy flow may exist on a specific finite collector. However, it only represents a certain constant differential amount of energy flow compared to the universal vacuum energy flow or some other flow reference point. It is like a whirlpool in the river. Energy is like the flowing water, and an "amount" of energy is like the amount of water in the collecting whirlpool form (between its input flow and its output flow) at any time. Obviously, energy (ordering) forms can come and go; the water flow itself remains. Any "magnitude of energy" is always a "trapped" amount of energy in a "collector" (form).

Decoupling Current Components and Utilizing d/dt

The two components of electron current dq/dt can be decoupled, by blocking the dm/dt component while allowing the d/dt displacement current to continue to flow. In our first paper, we pointed out one way: utilizing a special degenerate semiconductor material whose electron gas relaxation time is extended, providing a finite time during which the material serves as a charge (i.e., a charged particle) blocking device, while passing the flow of potential (the d/dt massless displacement current component) and restraining the mass displacement current component dm/dt. With the advent of Fogal's semiconductor, the process becomes much easier to obtain and utilize in practical machines and circuits.

In our second paper, we pointed out a second way: utilize an ordinary capacitor and ramp-up step-charging. We found, however, that in most ordinary capacitors, the capacitive aspect is defeated by the sloppy movement of the plates and dielectric, converting d/dt into dq/dt. Only a few very carefully selected capacitors are sufficiently rigid and can provide overunity. One must use rigidized calibration standard capacitors for the ramp-charging by series steps method to be successful. With ordinary capacitors, however, one can readily demonstrate that the efficiency can approach 1.0 rather than 0.50 as expected.

Overunity Secrets: Charge Blocking, Collection, Shuttling, and Two Isolated Circuits

The charge (actually charged mass) blocking approach provides a massless, free flow of vacuum EM energy that can be directed to a collector (capacitive or inductive) where it can be stored in either an E-field or a B-field. This stored energy can then be transferred to an isolated load circuit whose electrons (and hence their dm/dt mass displacement current) are free to flow as dq/dt. In the isolated load circuit, then, the two components [(d/dt)(dm/dt)] again couple to form i = dq/dt = [(d/dt)(dm/dt)], powering the load. All work in an electrical circuit is due to the mass displacement current dm/dt component; the massless displacement current (d/dt) is a flow of pure energy transport without loss, as is well-known. (For example, see Reference 4.)

Therefore, the first major free energy secret is simply to block the "working" component dm/dt of the current dq/dt while allowing the excess "lossless energy flow" component d/dt to flow to collectors to produce either free E-field or free B-field thereupon.

The second major secret is to transfer the collected excess free energy (via energy shuttling) to a second, isolated, load circuit, where the energy is discharged through the load in the conventional fashion (i.e., such that the two current components are coupled, and electron current i = dq/dt occurs through the load). The second circuit must be isolated from the original collection circuit, so that none of the load electron current dq/dt passes back through the original source, against its back EMF.

Should the grounds be the same between the load circuit and the collection circuit so that load electron current is returned through the back EMF of the primary source, then exactly as much excess work will be done inside the source to dissipate its separation of charges as was done in the external load to furnish useful work and in the external losses. In that case, overunity is destroyed, because one is using one-half the excess free energy to destroy the source faster, while the remaining half is distributed among all external loads and losses. Since there are always some external losses besides the load, then the ratio of load power to source dissipation power is always less than unity in a conventional closed-loop circuit containing both load and source. Hence the necessity for utilizing two isolated circuits: one where energy is collected freely from the source, and one where energy is dissipated as work in the load without dissipative work in the source, and energy shuttling between them.

A Simple Open-Loop Overunity Device

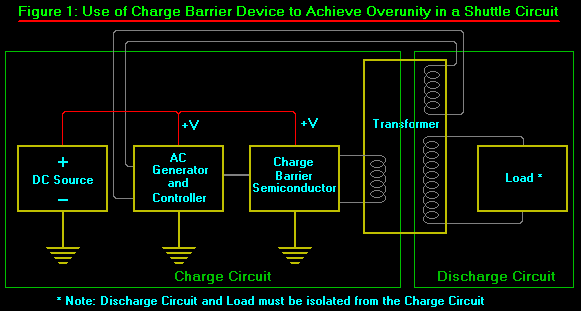
Figure 1 shows a very simple but very powerfully amplified overunity device, using an AC charge blocking semiconductor (CBS) (such as a Fogal semiconductor). The gist of the circuit is that an AC source furnishes AC current dq/dt to the CBS, which uses some of the power to power itself, but then blocks the dm/dt portion of the dq/dt input current, passing only the massless displacement current component (d/dt) into its output circuit. The (d/dt) output of the CBS is fed through the primary winding of a transformer, in this case a step-up transformer. The "current gain" of the CBS will depend upon (1) the load connected to it, and (2) the ability of the CBS to continue to block the increasing E-field on its trapped charges, as more free energy flow (d/dt) is drawn through it by the load. Thus the load and the CBS must be matched within the operational ability of the CBS, so that the CBS does not fail catastrophically.

In the primary winding of the transformer, the (d/dt) displacement current produces a magnetic field H, storing the excess flowing energy in that field. This is a normal magnetic field; all magnetic fields are produced by the (d/dt) component of the current anyway. This magnetic field, as it changes, couples to the secondary winding, producing a normal magnetic field H therein by normal means. In the secondary circuit, electrons are not restrained by a CBS. Hence the (d/dt) induced in the circuit on the secondary side couples to the unrestrained electrons, producing normal electron current dq/dt, and driving it through the load to power it. Note that energy is conserved across the primary and the secondary; however, dissipative power and work (energy loss rate and energy loss) are not conserved, because a free flow of lossless excess energy in the form of displacement current is flowing from the vacuum through the source antenna, thence to the CBS, through it to the primary of the transformer and into the primary magnetic field, through it to the secondary magnetic field, through it into the (d/dt) induced in the secondary circuit and coupled to the electrons, through the resulting dq/dt into the load, where the scattering of photons as heat dissipates the free flowing energy in the displacement current d/dt component flowing through the load as a component of dq/dt = (d/dt)( dm/dt) = (d/dt)(dm/dt).

Free "Power" Amplification

If one places an ammeter in the output from the CBS, between it and the primary winding of the step-up transformer, one will read the (d/dt) as normal dq/dt in the ammeter itself. If one calculates the "free power" (i.e., the rate of energy dissipation) that is going into the transformer primary using this as the "current," one will show that energy and "power" are conserved between primary and secondary of the transformer. However, the actual dissipative power going into the primary side is zero or, in real circuits, vanishingly small. Consequently, the device has a very high variable power gain that depends upon the rate of energy draw and dissipation of the load on the secondary side. If one adds more load, one draws more dq/dt current on the secondary side, hence more excess d/dt displacement current on the primary side. The overall "power amplification" is limited by the ability of the transformer to handle the power in the secondary and the ability of the CBS to withstand the pressure of the internal charge barrier. This device can be easily "close-looped."

The Negative Resistor: A Close-Looped "CBS and Shuttle" System

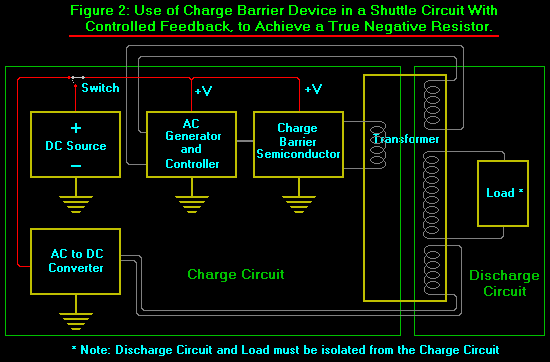
Figure 2 shows the close-looping of the device shown in Figure 1, in such manner that, once stable operation is underway and the load and input stabilized, the ordinary power supply for the CBS can be switched out of the circuit. In this case, the circuit operates as a self-powered overunity device; i.e., as a negative resistor.

A normal resistor receives an ordered energy flow from its external circuit and scatters this energy as work out to the vacuum. I.e., it receives i = (+)/dt(dm/dt) (scatters the excess ()/dt component (i.e., of the dq/dt passing into it from the high potential side) by radiating it away to the surrounding vacuum as scattered photons (heat)), and outputs inert (no excess () component) electron current dq/dt into the ground side.

A negative resistor does exactly the opposite: it accepts inert incoming electrons from its "ground" side, also accepts incoming (converging) d/dt energy from the vacuum as virtual photons being absorbed upon these inert electrons so that a is added to the electron current, creating an excited, excess energy-carrying i = (+)/dt(dm/dt), and passes this excited current out of its high side and out into the external circuit to power the circuit. In other words, the negative resistor becomes a self-contained free power source, once brought up to stable operation.

In Figure 1, all that needs to be done is simply to extract some of the secondary power and feed it back to create the power input consumed by the CBS and the other normal components of the primary circuit side of the transformer.

Multitaps can be added to the secondary side, to provide varying voltage power supplies for loads requiring different voltages.

Energy is conserved in the device, because it always functions as an open circuit, receiving excess energy from an external source (the surrounding vacuum, in its virtual photon exchange with the charges in the system). It is far from thermodynamic equilibrium, and classical thermodynamics (including the second law) does not apply.

It is simply a continuous free power supply: it is a negative resistor. Far more complicated units can be designed and produced. The basic point is that this type of overunity power supply is continuous and self-powered, driven by the violent exchange of energy from the vacuum, and simply collecting and gating some of that energy to the load to power the load.

Conclusion

With this third paper, we complete the triad of papers we set out to write a little over a year ago. With the availability of charge barrier devices such as the Fogal semiconductor, together with the collection, shuttling, and use of free d/dt flowing energy, the Age of Free, Clean, Electrical Energy has finally dawned.

Let us use it wisely, and for the betterment of humankind, not for its destruction.

[Support of portions of this research by A.D.A.S. is gratefully acknowledged.]

References and Notes

1. Bearden, T.E., Feb. 9, 1993, "The Final Secret of Free Energy," ADAS, distributed over Internet. The paper was also published in Magnets, 7(5), May 1993, p.4-26, in Explore!, 4(3/4), 1993, p.112-126, and in several other media. See also Bearden, T.E., "Additional Information on the Final Secret of Free Energy," Feb. 15, 1994, distributed on Internet.

2. For proof that an ordinary capacitor can be charged almost without entropy, see Fundaun, I., C. Reese, and H.H. Soonpaa, "Charging a Capacitor," American Journal of Physics, 60(11), Nov. 1992, p.1047-1048. See also Calkin, M.G. and D. Kiang, "Entropy change and reversibility," American Journal of Physics, 51(1), Jan. 1983, p.78-79. See also Heinrich, F., "Entropy change when charging a capacitor: A demonstration experiment," American Journal of Physics, 54(8), Aug. 1986, p.742-744. See also Gupta, V.K., Gauri Shanker, and N.K. Sharma, "Reversibility and step processes: An experiment for the undergraduate laboratory," American Journal of Physics, 52(10), Oct. 1984, p.945-947.

3. In most texts, the treatment of displacement current is far from adequate. A better treatment than most is given by Krauss, John D., Electromagnetics, Fourth Edition, McGraw-Hill, New York, p.437-439, 547-549. This treatment must still be augmented by treatment from other texts, and the ensemble "synthesized." Even then, it will never be completely clear until the separation of mass from the massless charge, and separate accounting of the two, is accomplished in the manner pointed out by the present paper.

4. For a typical confirmation that massless displacement current is already known to be lossless transport of energy without entropy, i.e., without work, see Buchwald, Jed Z., From Maxwell to Microphysics, University of Chicago Press, Chicago and London, 1985, p.44. Quoting: "...no energy transformation into heat occurs for displacement currents." It should be obvious from this fact alone that the proper way to accomplish overunity in electrical devices is to utilize the massless displacement current to flow and store excess energy, then use a "heat pump" type cycle to transfer the collected energy to a separate load circuit and discharge it separately in the load.

5. For a very recent proof that the potential is a flow process, and in fact consists of bidirectional EM waves, see Hsue, C.W., "A DC Voltage is Equivalent to Two Traveling Waves on a Lossless, Nonuniform Transmission Line," IEEE Microwave and Guided Wave Letters, 1993, Vol. 3, p.82-84.

6. For proof that the vacuum EM zero-point energy is continually produced by a cosmological feedback from every charged particle in the universe, see Puthoff, H.E. , "Source of Vacuum Electromagnetic Zero-point Energy," Physical Review A, 40(9), Nov. 1, 1989, p.4857-4862.

7. For proof that in theory the vacuum energy can be tapped, see Cole, daniel C. and Harold E. Puthoff, "Extracting Energy and Heat from the Vacuum," Physical Review E, Vol. 48, No. 2, Aug. 1993, p.1562-1565.

8. For proof that a higher topology examination of EM phenomena allows energy collection as potentials and energy shuttling in circuits, see Barrett, T.W., Annales de la Fondation Louis de Broglie, Vol.16, No. 1, 1991, p.23-41. Barrett shows that EM expressed in quaternions allows shuttling and storage of potentials in circuits, and also allows additional EM functioning of a circuit that a conventional EM analysis cannot reveal. He in fact shows that Tesla's patented circuits did exactly this.

9. Stoney, G.J. (1897) "XLVII. On a Supposed Proof of a Theorem in Wave Motion, To the Editors of the losocal Magazine," losocal Magazine, 5(43), 1897, p.368-373. Stoney first pointed out the bidirectional EM wave decomposition of the scalar potential.

10. Whittaker, E.T., "On the Partial Differential Equations of Mathematical Physics," Mathematische Annalen, Vol. 57, 1903, p.333-355; "On an Expression of the Electromagnetic Field Due to Electrons by Means of Two Scalar Potential Functions," Proceedings of the London Mathematical Society, Series 2, Vol.1, 1904, p.367-372.

Comments

There are no figures to the paper "Background for Pursuing Scalar Electromagnetics". I had envisioned preparing a book along that vein, with many, many figures, etc., but simply have not had time to start the project.

Further details about the coupling of virtual flux:

What I have begun is a "disassembly" of classical EM theory, separating the fundamental entities that are massless from those that have mass. When Maxwell wrote his theory, everyone knew that the vacuum was filled with a thin material fluid -- the material ether. Maxwell incorporated that as a fundamental assumption of his theory. In other words, the scalar potential already consisted of "thin fluid". Hence electrical charge was "material". (At the time, the prevailing view of electricity was as a thin material fluid, flowing through wires like water through pipes). Consequently, classical EM was modeled completely in terms of fluid dynamics, and everything was material. The notion of charge q then was just a small piece of the material liquid electricity. In other words, it was not a system of finer constituents. Maxwell's theory was in quaternions, and consisted of some 20 equations in 20 unknowns (Nahin's count). A great number of different potentials arose in that theory, potentials which no one had the slightest notion as to what they were.

Heaviside (and to a lesser extent Hertz and Gibbs) reduced the algebraic topology of Maxwell's quaternion model to vectors, which is a seriously curtailed mathematics compared to quaternions. Heaviside also hated potentials because he could not understand what they were. Consequently, he got rid of as many as possible. He also focused attention of the electricians upon the notion of external forces pushing upon masses and "creating all the action". Again, this notion prevailed all of science at the time - and unfortunately still prevails in physics today. It is absolutely, unequivocally false. It is from Man's primitive experience, of pushing and pulling on objects. It is a fact that mass is always a component of force. The rigorous definition of force may be taken as F dp/dt = d/dt(mv). From this definition, if there is no mass, there is no force. (Suitable quotes from leading foundations physicists can also be given, of course). Instead, there is at best dF/dm. Quantum mechanically, all mechanical and EM forces are generated on and off the affected mass by an exchange of virtual photons. It is the coupling of the virtual photon flux of the vacuum to a particle of mass that produces a charged particle. [It is a spatial asymmetry in that coupled flux exchange that, together with the coupled mass, produces a force]. The "charge" is the coupled virtual photon flux, not the mass. Consequently, our old friend q is actually a system defined by:

q _q m_q
[Equation 1]

where the operator means "coupled to" or "trying to couple to", representing the virtual photon flux aspect, and does not represent multiplication. From [1], one easily obtains the expression for normal current i by time differentiating, so that:

i dq/dt d/dt(_q m_q) = (d_q/dt)(dm_q/dt)
[Equation 2]

We now see that, in an electric circuit, there are actually two "currents" represented by the normal current dq/dt. There is the massless displacement current (d_q/dt) component and there is the "mass of the electrons" current (dm_q/dt). Note that the operator is retained; in this case, it represents "is trying to couple" or "is coupling". In dq/dt, of course, the coupling is occurring.

It is well known that (d_q/dt) represents the flow of energy without loss. I.e., it is pure energy transport. Actually, the (dm_q/dt) in EM theory represents the drift current longitudinally through the circuit. That is the one in which the electron masses "progress" through the circuit, though at a feeble rate, typically on the order of 11 feet per hour or some such. The (d_q/dt) component moves at the speed of light. Now you can see the reason retaining the coupling operator . In a simple dq/dt current in a circuit, there is a continuous speed of light energy input to and energy output from the electrons that are sluggishly moving along at the drift velocity. The electrons are actually moving much, much faster from side to side due to precession caused by their spin and the continual dE/dt being created on them by the coupling and uncoupling of the (d_q/dt). In a given current loop, one can also show that the (dm_q/dt) component is always the work (scattering of energy) in the loop.

When the Michelson-Morley experiment destroyed the material ether, Maxwell was already dead. Heaviside (and to an extent Gibbs) was just producing his own vector curtailment of Maxwell's theory. So nothing at all was done to the EM theory to remove its assumption on the material ether. Not a single equation was changed. A short debate ensued about 1980 or so, mostly in Nature, and the vectorists simply "threw out" the quaternionist model as being far too difficult for engineers and far too abstract. Remember, there were probably not more than about three dozen scientists in the world at that time who could have been considered "skilled" in EM theory.

To handle the negation of the material ether, electricians just simply announced "There is no ether, so we are not using one!" Not an equation was changed. No one had the slightest notion how to change them anyhow. And that's the classical EM we're stuck with today. It is riddled with errors. It desperately needs redoing. Since no one else seems to want to redo it, I've started work on the reformulation problem. Actually, the task needs a person with much greater mathematical "horsepower" than me, but one who still is willing to ponder deeply on foundations issues (most are not). However, I can do it; it will just take three or four years. There's no longer any problem in seeing what has to be done. Now, it's just a matter of doing it.

I would like to also clear up one thing for which I've been severely criticized by academics. Specifically, the charge has been leveled that "scalar interferometry" is an oxymoron. Well, it is not such in quantum mechanics. In addition, it is not an oxymoron anyway, on first principles. Stoney and Whittaker showed that any scalar potential can be decomposed into a set of bidirectional wave pairs, with the pairs in harmonic sequence. Each pair consists of a wave and its true time-reversed replica. So, the interference of two scalar potential beams is simply the interference of two hidden sets of multiwaves. That the waves in each beam are "hidden" is of no concern; mathematically, scalar potential interferometry is inviolate, in spite of the archaic assumptions of classical EM. Indeed, Whittaker's 1904 paper showed that any ordinary EM field, including EM waves, can be replaced by such scalar potential interferometry. Further, the source of interfering potentials need not be local. In other words, EM field gradients of any pattern desired can be created at a distance, by the distant interference of two scalar potential beams. I hope that this lays the problem of scalar interferometry to rest.

Further details on his papers on cancer:

All the cancer and healing papers were interim, and are upgraded by my two books AIDS: Biological Warfare,and Gravitobiology; and by my recent cancer paper (Cancer and the Unresolved Health Issues in the Biological Effects of EM Fields and Radiation) published by Tesla Book Company in 1993. Incidentally, the cancer paper published by Tesla Book Co. is a slightly upgraded version of the "Mechanism for Long-Term Cumulative Biological Effects of EM Radiation", presented to the Alabama Academy of Science, Mar 1993. Hard copies of all viewgraphs are also included in the paper. Tesla Book Co. address is P.O. Box 121873, Chula Vista, CA,91912. Their phone number is 1-800-398-2056 or 619-437-8515.

Further details about his patent application:

After filing the 1993 paper "The Final Secret of Free Energy" on Internet, I still had a year to patent the process. So in early February 1994, my associates and I filed a patent calling for the blockage of the mass flow of the electrons (by several schemes), while allowing the (d_q/dt) to pass and be collected. The collected excess energy is then shuttled onto a separate load circuit, where it is discharged normally through the load by dq/dt. This way, the energy is delivered to the load and discharged normally through it as power and work, but without driving a corresponding dq/dt back through the back emf of the original battery source.

Now with an additional year's work under our belt, we at CTEC also filed a formidable 200-page Continuation of our patent application on May 13, 1994. This filing is essentially a textbook on our approach to overunity electrical devices. Our continuation also formalizes the process of charge blocking and (d_q/dt) passage, together with energy shuttling between separate collection and work circuits, as means of achieving overunity. The process does not violate any of the laws of physics and thermodynamics. It is simply akin to the standard heat pump equations. The system is open and there is an external source of the excess energy; the problem is simply to collect the energy without dissipation, then shuttle it over to the load and discharge it there as work, without any of the discharge current (d_q/dt) being allowed to pass back up through the back emf of the battery/source. Two days after our Continuation filing, I presented the gist of that work at the 2nd International Symposium on New Energy (ISNE) of May 12-15, 1994, in Denver, Colorado (sponsored by The Institute for New Energy, (INE) and The International Association for New Science (IANS)). Videotapes and audio tapes were made for each presentations including mine and are available from Backcountry Productions, 831 Alpine Street, Longmont, CO, 80501, TEL: (303) 772-8358. I had permission by my CTEC Board of Directors to release the new material only after our continuation was filed. Consequently, since we successfully filed on 13 May 94, I took the next day and a half in my hotel room and feverishly hand-drew the major viewgraphs, got the transparencies made in the hotel's business center, then handcolored them with magic markers. I finished the last viewgraph about 2 hours prior to my formal presentation to ISNE. So the material in the presentation differs dramatically from the material in the Proceedings paper.

The 656 pages Proceedings can be ordered from both The International Association for New Science (IANS), 1304 South College Avenue, Fort Collins, CO 80524, TEL and FAX: 303-482-3731, and The Institute for New Energy, P.O. Box 58639, Salt Lake City, UT 84158-8639, TEL: 801-583-6232, FAX: 801-583-2963

Of course, you realize that the U.S. Patent Office will never grant us a patent on an overunity electrical device unless a working model is built and independently tested. We are pursuing that objective now. We are certainly making progress, but we have not as yet solved the relaxation time problem or the "rigid capacitor" problem. In fact, we have now extended our capacitor testing to include the very expensive laboratory calibration standard capacitors, and have proven that all of them reconfigure when charged. In other words, every capacitor presently available is not just a capacitor, but is first an energy-to-work transducer. The current dq/dt is drawn to provide the work to forcibly drive the physical reconfiguration. Indeed, the precision $2,000 or more calibration standard capacitors actually contain precision springs! So the electrical energy is converted to mechanical work, then back to electrical stress energy. In a standard closed circuit loop back through the source, the production of the reconfiguration work in the capacitor destroys any chance at overunity. The reason is that the same current dq/dt that moves into the capacitor to do the reconfiguration work is also forcibly rammed back up through the back emf of the source, doing an equal amount of degradation work inside the source. When the forcing V is removed and the capacitor connected across a load, it again reconfigures. One recovers the mechanical stored energy as electrical energy due to a piezoelectric-type effect in the reconfiguring materials. But the reconfiguration work, whose twin and equal is also done in the source, has already defeated the ability to store the energy on the capacitor "for free". Instead, you already do not have an "excess" stored there, over and above the degradation of the source. The capacitive method of storage depends upon a true "charge-blocking" capacitor which does not reconfigure.

There is not now, and there never has been, a truly electrical capacitor.

The only candidate presently is the solid chip capacitor built into Fogal's charge blocking semiconductor (patented in 1993). That semiconductor is now being tested. If it tests out, then a demonstration model for our patent application will be fairly straightforward, as outlined in our continuation. Otherwise, demonstration of successful overunity with our methodology will still require substantial work before we succeed. That's the present status of our work and our progress, and our patent application.

We are encouraged, however. There are always two questions in research: (1) Can this in theory be done? and (2) if so, how difficult is it? What are the specific tests? What are the resources needed? etc. Unless one has a clear "Yes!" to the first question, one is still scouting the territory for an effect. So one cannot legitimately ask the second question at all. On the other hand, once the first question can be clearly and unequivocally answered "Yes!", then the first question need never again be asked. Instead, one now is dealing with exploratory development and engineering development. In other words, it is known it can be done. It is just a matter of doing it, which still may be a difficult task. Our status is that we have clearly and unequivocally gotten a resounding "Yes!" to the first question. We are now directly in the second series of questions. So we know it can be done along the lines we are pursuing. But nature still demands its payments; we still have to actually get it done and prove it.

As a result of the rather catastrophic aerospace layoffs here in Huntsville, I've retired and am continuing as best I can on a much-reduced budget. We (CTEC) will succeed or fail on the bench. And it will be an honest success or failure. We are also openly sharing all our progress, or lack thereof, and the theoretical approach we are using. That's all that anyone can do and call it scientific method.

I hope this answers all your questions. Good luck and I do appreciate your efforts in placing this material on Compuserve to be available to many more engineers and scientists.

Sincerely,

T.E. Bearden
August 16, 1994

(The audio tapes cost approx $10 each, and the video tapes cost approx. $25 each including postage. The Proceedings cost $50 plus shipping & handling)

If anyone finds more up-to-date info about Bearden's work, I would certainly like to hear about it!

Alain Beaulieu Compuserve: 70403,3645
Internet: nstn1142@fox.nstn.ns.ca