Back to My Programs Teksture lesa

 

1. Definicija naloge

2. Potek resevanja
    2.1 Opis rasti drevesa
    2.2 Simulacija rasti drevesa

3. Zajem slike

4. Upravljanje s programom
    4.1 Zapis slike

5. Detajli programa
    5.1 Inicializacija grafike
    5.2 Komunikacija z uporabnikom
    5.3 Nastavitev barvne palete, zajem in prenos slike

6. Zakljucek

7. Reference

Definicija naloge

Izdelati je treba program za generacijo teksture lesa, in zapis slike v uporaben slikovni format.

Potek resevanja

Opis rasti drevesa

Z zeljo, izdelati program, ki generira dovolj realisticne teksture lesa, moramo simulirati rast drevesa, torej poznati dolocene parametre, po katerih se drevo ravna pri rasti. Ker se jo da najlepse matematicno popisati in ima najmanjsa odstopanja, izberemo smreko.

Drevesa rastejo v stozcih, v nasem primeru (smreka) je razmerje med visino in polmerom 80:1. Polmer zacetne vejice ali debelina letnice v prihodnjosti je odvisna od preskrbljenosti drevesa. Po opazovanjih lahko dolocimo, da se debelina letnice pri smreki giblje med 1.5 in 3.5 mm. Letnica poganja spomladi, ko je dovolj hrane, v svetlo rjavi barvi, ki se pozno v jeseni naglo spremeni v temno rjavo. Vrh enoletnega poganjka se pri koncu rasti razveja v zasnove novih vejic. Naslednje leto se obstojeci stozec oblece v novo plast lesa, oblecene zasnove vejic pa so novi stozci. Medtem ko drevo raste v razmerju 80:1, rastejo veje v razmerju priblizno 32:1. Poleg tega moramo upostevati, da na spodnji petini debla, zasnove vej z rastjo pocasi zamrejo. Polmer stozcev z visino ne pada konstantno, ampak niha okrog premice konstantnega manjsanja z amplitudo do 3 mm in periodo 0.5 m. Zaradi ovir, ki se pojavljajo v blizini drevesa (stene, druga drevesa), se debelina letnic spreminja tudi tangencialno, ne le radialno tako, da lahko pricakujemo najvec 15% ekscentricnost debla. Na spodnji sestnajstini debla, zacenja deformacija debla v radialni smeri naglo narascati, bolj ko se blizamo korenikam.
 

Simulacija rasti drevesa

Program za generacijo tekstur lesa potrebuje vhodni podatek o starosti dreves. Najvecja starost, ki jo dovoli program, je 127 let.Program rezervira polja 127 debelin letnic, 127 radijev letnic, in 127 visin letnih stozcev, 127 x 7 kotov in visin vej. Program generira drevo, ki raste ob koordinatni osi x v pozitivno smer, enote so v metrih.

Najprej se generira nakljucna serija debelin letnic, katere se nato sestejejo v radije posameznih let, le ti pa z mnozenjem definirajo vrhove posameznih stozcev ob osi x. Na vrhu vsakega stozca se izbere nakljucno stevilo vej, ki bodo pognale tega leta (0 do 7), polni krog se razdeli na enakomerne dele stevila vej. Na to enakomerno kotno razporejenost vej po obodu, se veje nakljucno zamakne +/- 20°. Poleg tega se veje nakljucno zamakne od idealne visine (vrha stozca) +/- 5 cm. Nazadnje se izbere nakljucno ekscentricnost debla (do 15 %). S temi parametri je deblo popolnoma popisano.
 

Zajem slike

Sliko zajamemo na presecni ravnini debla. Ravnina je popisana s tocko [XYZ], to je koordinato centra ekrana, ter z normalnim vektorjem ravnine. Le ta je dolocen s kotom [j] med projekcijo normale na ravnino XY in osjo X ter s kotom [J] med ravnino XY (oz. projekcijo normale) ter normalnim vektorjem (horizontalni kot normale ravnine ter elevacijski kot normale ravnine). Poleg tega s povecevalnim parametrom [Zoom] dolocimo ogljisca ekrana.

Zajem slike poteka za vsak piksel ekrana posebej. Skeniramo vrstice od vrha proti dnu in piksle od leve proti desni. Koordinate vsakega piksla [ij] posebej preracunamo v koordinate drevesnega koordinatnega sistema [xyz] po formuli:

I = (i-320) J = (j-240)

x = X + (sin(j)*I + sin(J)*J* cos(j))*Zoom/320

y = Y - (cos(j)*I - sin(J)*J* sin(j))*Zoom/320

z = Z - (cos(J)*J)*Zoom/320
 


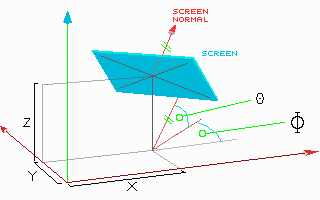
Screen Layer presentation


Stevilke 320 in 240 veljajo za graficni nacin 640x480.

Ko se dolocijo koordinate posameznega piksla, se poisce barva le tega. Paleta barv jelovega lesa se nahaja linearno razporejena med RGB tockama [68 3C 00] in [D4 A4 2C] hex. Robni barvi sem dolocil vizualno ob primerjavi lesa. (Velja za paleto TreePal0.COL) Glede na to, da najnatancnejsi graficni nacini delujejo v RGB direktnem nacinu 8:8:8, se da v RGB prostoru koordinatne osi R,G in B razdeliti na najvec 256 delov. Ce v to RGB kocko postavimo daljico, bo ta daljica imela svojo dolzino glede na koordinatne osi Dr Dg in Db. Le v redkih primerih bo katera od dolzin Dr Dg Db dolga 256 enot. Palete cistih barv rdece, zelene, modre, rumene, turkizne, violicne ter sive bodo imele eno dve ali vse tri stranice dolge 256 enot. V nasem primeru pa je razpon Dr Dg Db [+108 +104 +44] dec. Ker je koordinatni sistem RGB celostevilcen sledi, da nam lahko daljica priskrbi le toliko razlicnih barv, kot je dolga njena najdaljsa diferenca plus ena, v nasem primeru je to 109 barv. Zapis slike, katere paleta se nahaja le na daljici, s komponentami RGB bi bil zato potraten iz razlogov velikosti, kompresibilnosti ter hitrosti izrisovanja. Zato sem se odlocil za graficni nacin z 256 fiksnimi barvami 640x480x256.
 


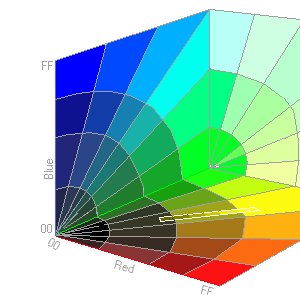
RGB space presentation


Barva posameznega piksla se torej doloci glede na njegove koordinate [xyz]. Koordinati y in z se pretvorita v oddaljenost od osi X, [r 2]= y 2 + z 2, poleg tega pa se v kot y = arctg(y/z) na ravnini YZ. Nato se glede na koordinato [x] in kot [y] poisce tisti zaporedni stozec, katerega radij ne presega oddaljenosti piksla od osi X. Glede na odstotek oddaljenosti piksla od notranjega stozca glede na zunanji stozec, se pikslu doloci barva iz palete (0% = 255, 100% = 1).

Radij posameznega stozca je odvisen od koordinate x: R(x) = (R[i] - (x/80))

Ta radij modificiramo z nihanjem po visini: R(x) = R(x) * (1 + (sin(4*P*x)*0.033))

ter z ekscentricnostjo: R(x) = R(x) * (1 + sin(y)*Exc)

Upostevajmo se vpliv korenik na deformacijo oboda: R(x) = R(x) * (1 + root*0.3*xx55)

xx = (1 - x/H[max]) kjer je H[max] visina zadnjega, zunanjega, najvisjega stozca.

R(x) = R(x) * [mul] Zadnji faktor, katerega moramo upostevati so veje. Veje sem simuliral tako, da sem na dolocenem obmocju okrog veje multipliciral vse radije stozcev. Multiplikacijski faktor je odvisen od modificiranega kota [j] med vektorjem veje in vektorjem izhodiscne tocke veje na osi X proti tocki [xyz]. Upostevajo se vse bliznje veje tako, da se njihovi faktorji med seboj mnozijo. Zacetni multiplikacijski faktor veje je mul = 1. Tega pomnozimo s preostalimi faktorji, ki so, ce je kot [j] manjsi od 0.65 rad (1 + 32*e-26*j), drugace pa 1

Z vsemi temi multiplikacijskimi faktorji smo deformirali stozce tako, da smo dobili obliko drevesa. Obstaja se en multiplikacijski faktor, ki zadeva barvo in sicer. Barva v vejah je temnejsa, ker so tu letnice debelin [0.4 .. 1.2] mm in se njihova barva ne razteza cez cel razpon od svetle do temne. Zato dodamo barvni multiplikator Cmul = mul16 , ki zagotavlja potemnitev grc.
 

Upravljanje s programom

Program deluje v okolju DOS in potrebuje dva vhodna parametra: Za paleto barv se smatra, da so barve podane v 6-bitni globini, zaporedje RGB (zaradi programa s katerim sem generiral paleto), program pa inicializira grafiko 640x480x256 na standardno SVGA 6-bitno globino palete.

 Pri zaganjanju programa le ta zapisuje mozne probleme v datoteko TREE.ERR. Med tekom programa se da spreminjati parametre ravnine:

Za zajem slike 640x480 potrebuje program na 80486 33MHz cca. 13 minut, na 80586 300 MHz pa cca. 1 minuto. Zaradi tega takoj po spremembi zgornjih parametrov opravimo preliminarno risanje 80 x 60 pikslov, ki se razmazejo na povrsino 8x8. Slika je zato grda, vendar se kalkulacija na Pentiumu opravi tako rekoc takoj. Ko zaslutimo, da smo nasli zeljeni prerez, sliko fino spoliramo.  Ko je slika spolirana, jo shranimo v nekompresiran format TarGA 640x480x256 pod vpisano ime. Vse shranjene slike bodo nosile inkrementirane indekse.  Kot receno traja poliranje eno minuto. Medtem, ko procesor opravlja idealni loop in preverja tipke, lahko izstopimo v DOS po regularni poti. Ta pot ne bo delovala med preracunavanjem.  Ce iz katerega koli razloga program obvisi ali ne zelimo cakati konca izracuna, lahko prisilno izstopimo v DOS pod pogojem, da ni prislo do napake med klicanjem interrupta tipkovnice.

Zapis slike

Sliko sem se odlocil zapisati v format TarGA, ker sem ga ze prej poznal. Format targa je nekompresiran graficni format z 256 barvnim in dirketnim RGB nacinom zapisa.

Zgradba:
 
Velikost
Stevilo
Opis
byte
12
glava
word
1
sirina X
word
1
visina Y
byte
2
glava
3byte RGB
256
paleta
byte
X * Y
slika

Detajli Programa

Inicializacija grafike

Grafiko sem inicializiral preko VESA BIOS interrupta. Zaradi napredka racunalniske tehnologije smatram, da imajo vsi racunalniki graficno kartico, ki podpira zeljeni graficni nacin, zato sem preverjanje oklestil iz procedure.

Komunikacija z uporabnikom

Komunikacija poteka preko tipkovnice. Zaradi enostavnejsega zaznavanja pritisnjenih tipk sem ze pred casom napisal proceduro, ki se izvede vsakic, ko tipkovnica generira interrupt (sprememba stanja na tipkovnici). Sprva je procedura shranjevala do 5 tipk, vendar sem zaradi nesmotrnosti proces poenostavil na dve katerikoli tipki. Dokler je neka tipka pritisnjena, bo njena modificirana koda shranjena v Command.Keys[0/1]. Pazljivost velja za tipko Pause, ki se obnasa drugace in jo je treba po uporabi "rocno" izbrisati iz spremenljivke - oznaciti prosto mesto. Procedura zaznava posebej status tipk Ctrl, Alt in Del, in sicer v spremenljivki Command.Release[2] oznacuje bit 0 stisnjen Ctrl, bit 1 Alt in bit 2 Del.

Nastavitev barvne palete, zajem in prenos slike

Nastavitev palete poteka preko VGA portov 0x3C8 in 0x3C9. Da bi se izognil pogostemu preklapljanju bank graficne kartice ter kasneje olajsal proces shranjevanja, sem se odlocil sliko izrisovati na virtualni zaslon (VGA.Virtual[i][j]), od koder se po koncu zajema z operacijo premika bloka prekopira v spomin graficne kartice ter nastavi novo 64 kb banko.
 

Zakljucek

Program sem prevedel z Watcom-ovim C/C++/Asm prevajalnikom. Program uporablja DOS4GW extender, ki preklopi procesor iz realnega nacina v zasciteni (proteceted) nacin. Posledica tega je, da se zacnejo namesto 16-bitnih registrov v procesorju uporabljati celotni (32-bitni) registri. Tako se za naslavljanje spomina ne uporabljajo vec 20-bitne kombinacije segmentnih in offsetnih registrov, ki nam lahko zagotovijo le 1 Mb spomina, ampak 32-bitni offsetni registri v kombinaciji s 16-bitnim selektorjem, s katerimi lahko naslovimo najmanj 4 Gb spomina.


Reference:
Miran Klemenc                                                                                                                           Ljubljana, 21. avg. 1998 1