LA PRIMERA TEORÍA DEL CAMPO UNIFICADO
¿QUÉ SON LAS DIMENSIONES?
¿POR QUÉ TRES?
LA TEORÍA DE KALUZA Y KLEIN
¿POR QUÉ ONCE?
LA GEOMETRIZACIÓN DE LA NATURALEZA
LA EXPLORACIÓN DE LAS DIMENSIONES OCULTAS

LA PRIMERA TEORÍA DEL CAMPO UNIFICADO

Buena parte de la fascinación de la física reside en que frecuente-
mente explica el mundo en términos de cosas que no vemos y que
quizá nunca seremos capaces de visualizar por mucho que forcemos
nuestra imaginación. Hemos visto ya varios ejemplos: el spin de las
partículas, la dualidad partícula-onda, y el espacio elástico. Hay quie-
nes consideran que estas abstracciones son exasperantes o incluso
indignantes; para otros son estimulantes e intrigantes. Aquellos que
gustan de la ciencia ficción nunca dejan de hallar en la nueva física una
mina de extrañas ideas.

Un ejemplo clásico del uso de conceptos abstractos para explicar la
naturaleza se dio en 1915, cuando Einstein publicó su sensacional
teoría general de la relatividad, uno de esos raros trabajos que señalan
un punto crucial en la percepción del mundo por parte de la humani-
dad. La belleza de la teoría de Einstein descansa no sólo en la potencia
y la elegancia de sus ecuaciones del campo gravitatorio, sino en el
arrollador radicalismo de sus bases conceptuales; porque Einstein no
sólo barrió de un plumazo la gravitación de Newton v su mecánica,
sino que abolió la noción misma de que la gravedad es una fuerza. La
teoría general de la relatividad establecía firmemente la idea de que la
gravedad es un campo de distorsión geométrica. Así, Einstein reducía
la gravedad a pura geometría. Donde antes había una fuerza que tiraba
a través del espacio, había ahora una "curvatura espacial".

La teoría de Einstein representó un cambio de perspectiva tan sen-
sacional que las demás fuerzas de la naturaleza fueron también some-
tidas muy pronto a un nuevo escrutinio. Por aquel entonces, la única
otra fuerza que había sido definitivamente identificada era el electro-
magnetismo. Ésta, sin embargo, no daba la impresión de parecerse en
absoluto a la gravedad. Además, había recibido ya una muy afortunada
descripción hacía varias décadas por parte de Maxwell, descripción de
la que no había ninguna razón para dudar.

Durante toda su vida, Einstein soñó en construir una teoría en la
cual todas las fuerzas de la naturaleza se fundieran en un solo esquema
descriptivo basado en la geometría pura. De hecho, dedicó una gran
parte de sus últimos años a la búsqueda de este esquema. Irónica-
mente, las mejores esperanzas que tenemos de realizar el sueño de
Einstein surgen del trabajo de un oscuro físico polaco, Theodor Kalu-
za, que ya en 1921 sentó las bases para un nuevo y audaz enfoque de
la unificación de la física.

Kaluza se inspiró en la capacidad de la geometría para describir la
gravitación y se propuso extender el trabajo de Einstein para incluir el
electromagnetismo en la formulación geométrica de la teoría de campo.
Quería conseguirlo sin alterar las sacrosantas ecuaciones electro-
magnéticas de Maxwell. Su labor es un ejemplo clásico de imaginación
creativa e intuición física. Kaluza comprendió que era imposible que la
teoría electromagnética de Maxwell pudiera convertirse en geométrica,
tal como entendemos normalmente la palabra, ni siquiera aceptando
las curvaturas espaciales. Su solución fue brillantemente simple. Am-
plió la geometría lo suficiente para acomodar la teoría de Maxwell. Lo
hizo de un modo que es a la vez extraño y persuasivo. Kaluza mostró
que el electromagnetismo es en realidad una forma de gravedad, pero
no la gravedad de la física familiar. Es la gravedad de una dimensión
invisible del espacio.

Los físicos ya estaban acostumbrados a considerar el tiempo como
la cuarta dimensión. La teoría de la relatividad revela que espacio y
tiempo no son en sí mismos cualidades físicamente universales. Al
contrario, deben ser unificados en una sola estructura tetradimensional,
llamada espaciotiempo. Kaluza fue más lejos y postuló que existe aún
otra dimensión, una dimensión adicional del espacio; hay así cuatro
dimensiones espaciales y cinco dimensiones en total. Pero entonces
Kaluza demostró que ocurre una especie de milagro matemático: El
campo gravitatorio de este universo pentadimensional se comporta
exactamente como la gravedad normal más el campo electromagné-
tico de Maxwell, al ser contemplado desde la restringida perspectiva de
las cuatro dimensiones. Lo que decía Kaluza con su atrevida conjetura
era que si ampliamos nuestra visión del Universo a cinco dimensiones,
entonces no hay más que un solo campo de fuerza, la gravedad. Lo
que llamamos electromagnetismo es tan sólo esta parte del campo
gravitatorio que opera en la quinta dimensión, la nueva dimensión
espacial que no habíamos reconocido.

La teoría de Kaluza no sólo amalgama gravedad y electromag-
netismo en una misma teoría, sino que ofrece una formulación geomé-
trica de los dos campos de fuerza. En su teoría, una onda electromag-
nética -por ejemplo, una onda de radio- no es más que una ondula-
ción en la quinta dimensión. El movimiento característico de las par-
tículas cargadas en los campos magnéticos y eléctricos se explica a la
perfección suponiendo que hacen cabriolas en esta quinta dimensión.

Visto de este modo, no hay fuerzas en absoluto, sólo está la curvada
geometría pentadimensional, con partículas que serpentean libremente
a través de un paisaje de estructurada nada.

El hecho de que, matemáticamente, el campo gravitatorio de Eins-
tein en cinco dimensiones sea exacta y completamente equivalente a la
gravedad más el electromagnetismo en cuatro dimensiones es a buen
seguro más que una coincidencia transitoria. De todos modos, la teoría
de Kaluza sigue siendo desconcertante en un aspecto fundamental: no
vemos la cuarta dimensión del espacio. El espacio de nuestras percep-
ciones es clara e inalterablemente tridimensional. Si el espacio posee
una cuarta dimensión, ¿dónde está? Antes de responder a esta pre-
gunta, conviene dejar completamente claro qué significa realmente el
concepto de dimensión.

¿QUÉ SON LAS DIMENSIONES?

Los escritores de ciencia ficción siempre han elogiado las dimen-
siones superiores del espacio. Muchos autores recurren a menudo a
"otras dimensiones" para trasladar a sus personajes de un lugar del
Universo a otro, evitándoles el tedio de atravesar el espacio normal de
tres dimensiones al relativo paso de tortuga de la velocidad de la luz.
En el libro de Arthur C. Clarke 2001: Una odisea del espacio, una ex-
pedición a Saturno termina penetrando en otra dimensión cuya puerta
de entrada se encuentra en una de las lunas de Saturno.

La fascinación que ejerce la dimensionalidad no empieza sin em-
bargo con la ciencia ficción. Los griegos apreciaban claramente su im-
portancia para la ciencia de la geometría. Un curioso ejemplo (que pone
de manifiesto los problemas de la dimensionalidad se refiere a las pro-
piedades de los polígonos regulares (figuras cerradas con lados iguales,
como cuadrados, pentágonos, octágonos, etc.). El número de polígo-
nos regulares es ilimitado, los hay de cualquier número de lados. En
cambio, hay solamente cinco tipos de poliedros regulares (cuerpos ce-
rrados cuyas caras son polígonos regulares). Como siempre, los griegos
insuflaron a su geometría un profundo sentido místico, y Tolomeo llegó
incluso a escribir un estudio sobre la dimensionalidad en el que argumen-
taba que la naturaleza no podía tener más de tres dimensiones espaciales.

En los tiempos modernos, matemáticos como Riemann desarro-
llaron un estudio sistemático de los espacios de dimensiones superiores
por su interés intrínseco. Un problema básico conque se encontraron
fue dar una definición satisfactoria de dimensionalidad. Esto era muy
importante, ya que los matemáticos deseaban probar teoremas sobre
las propiedades de los espacios con distintas dimensiones.
Intuitivamente, dividimos las estructuras geométricas en una, dos o
tres dimensiones, de acuerdo con la naturaleza de su extensión. Así, un
punto, puesto que no tiene extensión, es cerodimensional. Una línea es
unidimensional, una superficie bidimensional, y un volumen bidimen-
sional. Podemos citar las definiciones dadas por el propio Euclides,
aproxidamente en el año 300 a. de C.:

«Un punto es lo que no tiene partes.
Una línea es una longitud sin anchura.
Una superficie es lo que tiene solo longitud y anchura.
Un sólido es lo que tiene longitud, anchura y profundidad.»

Podemos conceptualizar mejor la bidimensionalidad imaginando
algún modo de etiquetar puntos en el espacio. Supongamos, por ejem-
plo, que deseamos encontramos con un amigo en un lugar predeter-
minado. Una forma de hacerlo es dando una longitud y una latitud;
podemos dar las coordenadas para el Empire State Building, por ejem-
plo. Esto nos deja todavía la libertad de especificar la altitud. ¿En qué
piso nos vamos a encontrar? En total, se necesitan tres números inde-
pendientes para definir un punto único en el espacio. Por esta razón se
dice que el espacio es tridimensional.

La teoría de la relatividad nos revelaba cómo el espacio está entre-
lazado con el tiempo; no debemos pensar sólo en el espacio, sino en el
espaciofiempo. ¿Cuándo vamos a encontramos con nuestro amigo en
el Empire State Building? Fijar el tiempo de un acontecimiento requie-
re un solo número -la fecha-, y así el tiempo es unidimensional. Jun-
tando espacio y tiempo, llegamos al espaciotiempo tetradimensional.

Si intentamos imaginar otras dimensiones, digamos una cuarta
dimensión espacial, la intuición falla. Podemos conseguir alguna ayuda
recurriendo a la analogía. Imaginemos una criatura bidimensional, un
ser destinado a pasar toda su vida confinado en una superficie. No po-
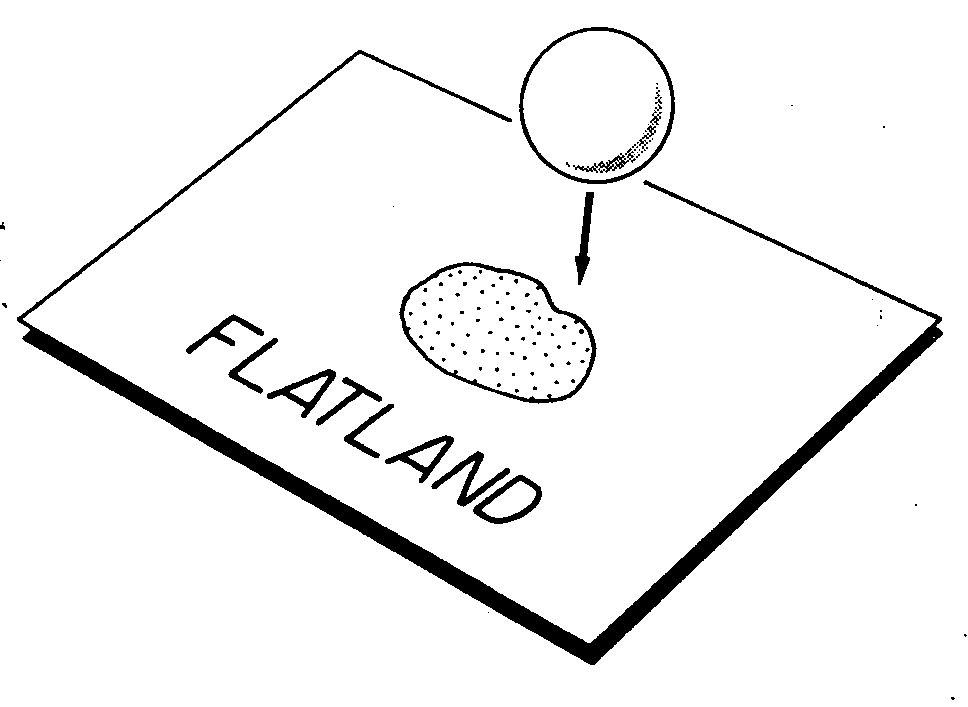
see ningún concepto del "arriba" y el "abajo". La figura 23 nos repre-
senta el universo de esa criatura. Podemos ver que la superficie, de
hecho, está inmersa en un espacio tridimensional, pero la criatura no
goza de nuestra amplia perspectiva y percibe tan sólo los aconteci-
mientos que ocurren sobre la superficie.

Figura 23. El universo bidimensional. Una criatura plana que viva en este hi-
potético Flatland o Planilandia no poseerá percepción ni del "arriba" ni del "aba-
jo". La bola que está a punto de atravesar su superficie será percibida como una
forma bidimensional cambiante.

Preguntémonos qué verá esta criatura cuando un objeto tridimen-
sional atraviese su superficie. La superficie corta una sección del obje-
to, sección que cambiará de forma y tamaño a medida que el objeto se
hunde. Una esfera, por ejemplo, se verá primero como un punto; lue-
go se ampliará a un círculo, aumentando de tamaño hasta alcanzar su
diámetro máximo; finalmente volverá a encogerse hasta transformarse
en otro punto y desaparecer. Objetos más complicados producirán
formas más complicadas.

Razonando por analogía, podemos suponer que las cuatro dimen-
siones de nuestro espaciotiempo se hallan englobadas en un universo
de cinco (o incluso más) dimensiones, cuya geometría no podemos
imaginar, pero que sin embargo posee una descripción perfectamente
lógica en términos matemáticos. Por supuesto, hace mucho que los
matemáticos extendieron las reglas de la geometría a espacios con
cualquier número de dimensiones (incluido el infinito). Es, pues, posi-
ble dar sentido a espacios de más dimensiones aunque sólo tres de
ellas se nos hagan manifiestas.

¿Qué rasgos poseerá un espacio tetradimensional? Un aspecto de
la dimensionalidad tiene que ver con el número de direcciones mutua-
mente perpendiculares que hay. La superficie de esta página, por
ejemplo, es bidimensional. Extendámosla plana sobre una mesa. Los
bordes de la página en una esquina definen dos líneas en ángulo recto.
Es imposible trazar una tercera línea que pase por esta esquina y sea
perpendicular a ambos bordes. Esta dirección, sin embargo, podemos
encontrarla si nos salimos del plano de la página y trazamos una línea
vertical. Así, en el espacio tridimensional -pero no en la superficie
bidimensional de la página- existen tres direcciones mutuamente per-
pendiculares.

En un espacio tetradimensional, es posible hallar cuatro direcciones
mutuamente perpendiculares. La figura 24 muestra lo que ocurre en
tres dimensiones, donde tres líneas rectas mutuamente perpendiculares
constituyen el máximo número posible.

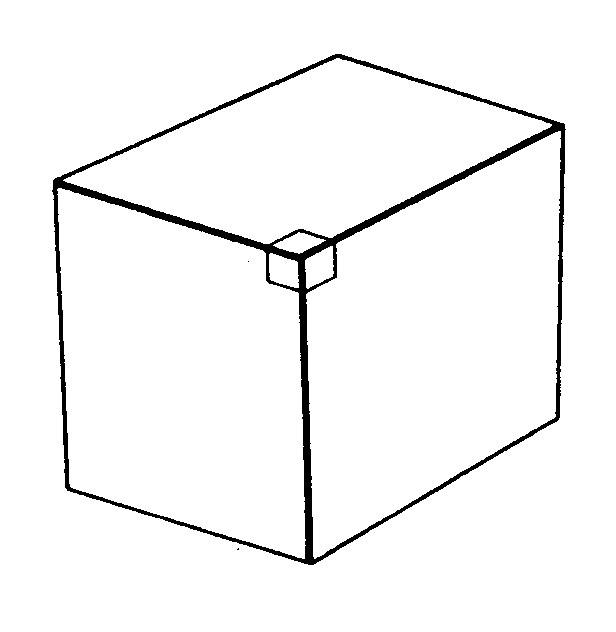
Figura 24. La aristas de un bloque rectangular forman tres líneas mutuamente
perpendiculares. En el espacio tridimensional de nuestras percepciones no
puede trazarse ninguna linea perpendicular a las tres.

Hagamos lo que hagamos, no podremos hallar una línea que forme un
ángulo recto con las tres dentro de los confines del espacio normal.
Cualquier línea perpendicular a las tres debe tener una dirección ajena a nuestro
espacio. Aunque no podamos imaginar dónde va esta línea, resulta claro que lógicamente esta línea puede existir. Podemos describirla. Sus propiedades
geométricas pueden ser evaluadas y catalogadas.

Un ejemplo simple de tales propiedades nos lo proporciona un
famoso teorema que se enseña en todas las escuelas de enseñanza
media, y que se debe al geómetra griego Pitágoras. El teorema habla
de los triángulos rectángulos. En la figura 25, las longitudes de los lados
del triángulo rectángulo son a, b y x. En símbolos, el teorema de Pitá-
goras afirma que esas tres longitudes están relacionadas por la simple
fórmula: x² = a² + b². Veamos un ejemplo: si sabemos que a = 3 y
b = 4, deducimos que x = 5, puesto que 5² = 3² + 4².

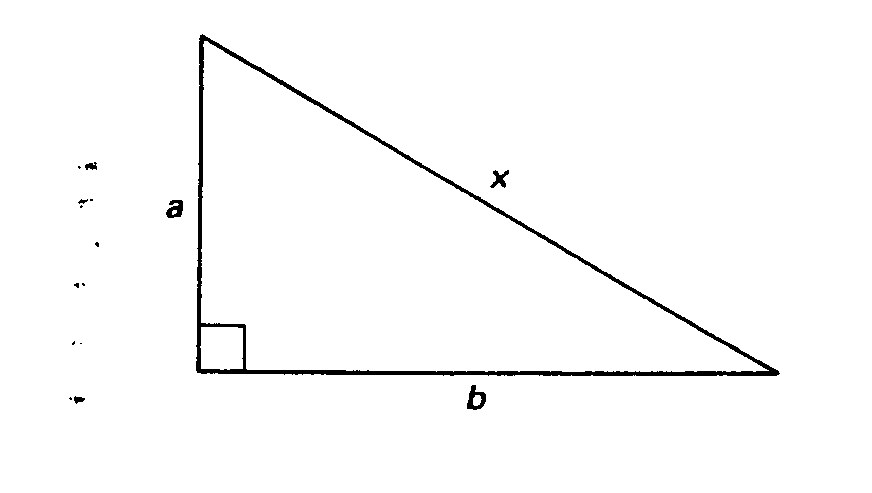
Figura 25. El famoso teorema de Pitágoras relaciona las longitudes a, b y x
de los lados de un triángulo rectángulo. Este teorema puece generalizarse
fácilmente a dimensiones superiores.

El triángulo de la figura 25 es, por supuesto, un objeto bidimensio-
nal, pero el teorema de Pitágoras puede generalizarse fácilmente a tres
dimensiones. En la figura 26 se representa una caja rectangular. Las
longitudes de los lados son a, b y c. El teorema hace referencia aquí a la
distancia en diagonal entre las esquinas opuestas de la caja, denotada
por x en la figura. En símbolos, el teorema de Pitágoras afirma ahora
que x² = a² + b² + c². La forma de esta ecuación es muy similar a la
del caso bidimensional, pero ahora necesitamos las longitudes de tres
lados mutuamente perpendiculares, a, b y c, para calcular la longitud
de la diagonal x.

En un espacio tetradimensional, la longitud de la diagonal deberá
calcularse a partir de cuatro longitudes perpendiculares, a, b, c y d.

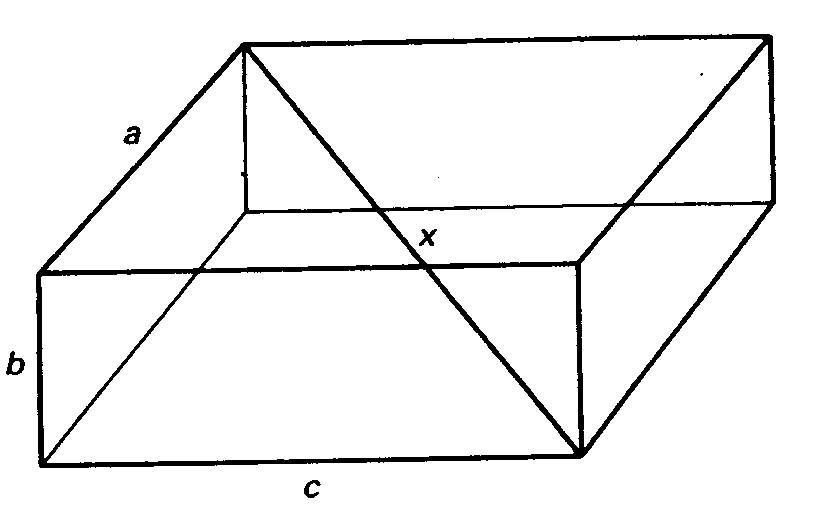
Figura 26. La longitud de la diagonal de la caja rectangular se relaciona con las
longitudes de los lados, a, b y c, mediante una generalización sencilla del
teorema de Pitágoras. Es fácil extender esta generalización a cuatro o más
dimensiones espaciales.

Tendremos entonces la fórmula x² = a² + b² + c² + d². De este modo,
aunque no podamos imaginar una caja tetradimensional, sí podemos
discutir sus propiedades geométricas.

Por muy valiosas que sean esas intuiciones geométricas, resultan
ser tan sólo un castillo de naipes. El castillo se derrumbó a finales del
siglo XIX, con el desarrollo de una poderosa rama de las matemáticas
conocida como teoría de conjuntos. Entre los sustos que recibieron los
matemáticos se encuentra el descubrimiento de Georg Cantor de que
hay tantos puntos en una línea como en una superficie. La idea intuitiva de
que una superficie es de algún modo infinitamente más rica en puntos que
una línea trazada en ella quedó completamente desacreditada. Esta sacudida
dejó incrédulos -incluso a matemáticos respetables. Algunos dijeron que Cantor
estaba loco. Charles Hermite escribió, desechando la idea: «Leer los escritos
de Cantor parece una verdadera tortura... La correspondencia entre una línea
y una superficie nos deja absolutamente indiferentes... tales arbitrariedades...
el autor hubiera hecho mejor esperando...», etc.

Hasta principios de siglo no se reparó el daño, al conseguir una
definición satisfactoria de dimensión. Las importantes contribuciones
de L. E. J. Brouwer, René Lesbesgue, y otros, establecieron finalmente
un procedimiento sin puntos flacos para comparar dos espacios y de-
cidir si poseían la misma dimensión. Estas pruebas se basan en ideas
sutiles y abstractas de la teoría de conjuntos que están muy alejadas de
intuición. Solamente con mucho cuidado y atención al detalle pueden
asegurarse los fundamentos lógicos de nuestra ciencia y de nuestra
experiencia.

¿POR QUÉ TRES?

Sea cual fuere la dimensión real del espacio, es indudable que sólo
tres dimensiones se hacen evidentes a nuestros sentidos. Muchos cien-
tíficos se han preguntado si es posible explicar por qué la naturaleza ha
seleccionado precisamente tres. ¿Es un número único en algún sentido?

En 1917 el físico Paul Ehrenfest escribió un ensayo titulado "¿De
qué modo se pone de manifiesto en las leyes fundamentales de la física
que el espacio posee tres dimensiones?" Ehrenfest dirigió su atención a
la existencia de órbitas estables, del tipo seguido por los planetas en
torno al Sol o por un electrón en torno al núcleo atómico. La omnipre-
sencia de las leyes de la inversa del cuadrado es bien conocida. En el
capítulo 5 vimos como las fuerzas gravitatoria, eléctrica y magnética
satisfacen todas ellas esta ley. En 1747 lmmanuel Kant ya reconoció la
profunda conexión entre esta ley y la bidimensionalidad del espacio.

Las ecuaciones que describen los campos gravitatorio o eléctrico pue-
den ser generalizadas fácilmente a otras dimensiones. Sus soluciones
revelan que en un espacio de n dimensiones tenemos que tratar con
una ley de la inversa de la potencia n - 1. Así, en tres dimensiones,
n - 1 = 2, y la ley es la inversa del cuadrado. En cuatro dimensiones,
n - 1 = 3, obteniendo así una ley de la inversa del cubo. Y así sucesi-
vamente. Puede demostrarse que si, por ejemplo, el Sol generara un
campo gravitatorio de la inversa del cubo, los planetas trazarían una
rápida espiral hacia él y serían absorbidos.

La situación con los átomos es similar. Aún teniendo en cuenta los
efectos cuánticos, resulta que los electrones no poseen órbitas estables
en espacios de más de tres dimensiones. Sin órbitas atómicas estables,
la química, y en consecuencia la vida, sería imposible.

Otro fenómeno que depende sensiblemente de la dimensión es la
propagación de las ondas. Se puede demostrar fácilmente que en es-
pacios con un número par de dimensiones una onda no se propagará
con nitidez, sino que producirá alteraciones con efectos de reverbera-
ción. Por esta razón es imposible transmitir señales bien definidas en
una superficie bidimensional como una lámina de caucho. Discutiendo
este tema en 1955, el matemático G. J. Whitrow llegó a la conclusión
de que la vida avanzada sería imposible en un espacio de dimensiona-
lidad par, ya que los organismos requieren una eficiente transmisión y
procesado de la información a fin de operar con coherencia.

Estos estudios no muestran la imposibilidad de otras dimensiones
espaciales, sino tan sólo que la física en un mundo no bidimensional
sería profundamente distinta y, con toda probabilidad, mucho menos
ordenada que en el mundo que percibimos.

¿Cómo encajar todo esto con la teoría de Kaluza de un Universo
con cuatro dimensiones espaciales? Una posibilidad es considerar la
nueva dimensión no percibida simplemente como un artificio, un truco
matemático sin significado físico. Sin embargo, poco después de que
Kaluza publicara su teoría original ya se propuso una idea más atractiva.

LA TEORÍA DE KALUZA Y KLEIN

En 1926, el físico sueco Oscar Klein encontró una respuesta mara-
villosamente simple a la pregunta de dónde había ido a parar la quinta
dimensión de Kaluza. Según Klein, no percibimos la nueva dimensión
porque, en un cierto sentido, se halla "enrollada" hasta alcanzar un
tamaño minúsculo.

La situación puede compararse a una manguera.
Vista desde muy lejos, la manguera parece ser tan sólo una línea sinuo-
sa. Un examen desde más cerca, sin embargo, nos revela que lo que
habíamos tomado por un punto en la línea es en realidad un círculo en
tomo a la circunferencia de la manguera (fig. 27). Supongamos, dijo
Klein, que así es nuestro Universo. Lo que normalmente tomamos por
un punto en el espacio bidimensional es en realidad un pequeño círcu-
lo en la cuarta dimensión espacial. Desde cada punto del espacio parte
un pequeño bucle en una dirección que no es arriba, ni abajo, ni a los
lados, ni ninguna otra en el espacio de nuestros sentidos. La razón de
que no observemos estos bucles es que su circunferencia es increíble-
mente pequeña.

Cuesta un poco habituarse a la idea de Klein. Parte del problema
reside en que no podemos imaginar dónde se enrollan esos bucles. Los
bucles no están dentro del espacio, extienden el espacio, del mismo
modo que una circunferencia avalando rápidamente forma un tubo.
Podemos imaginar fácilmente la situación en dos dimensiones, pero no
en cuatro. Sin embargo, la proposición sigue teniendo sentido. No hay
problemas con las órbitas estables o la propagación de las ondas, ya
que la materia y las ondas no pueden moverse libremente en la nueva
dimensión. La quinta dimensión puede estar aquí, pero no se puede ir
muy lejos en ella. Por supuesto, no hay ninguna posibilidad de utilizar
la teoría de Kaluza-Klein para acortar el viaje espacial; lo siento por los
escritores de ciencia ficción.

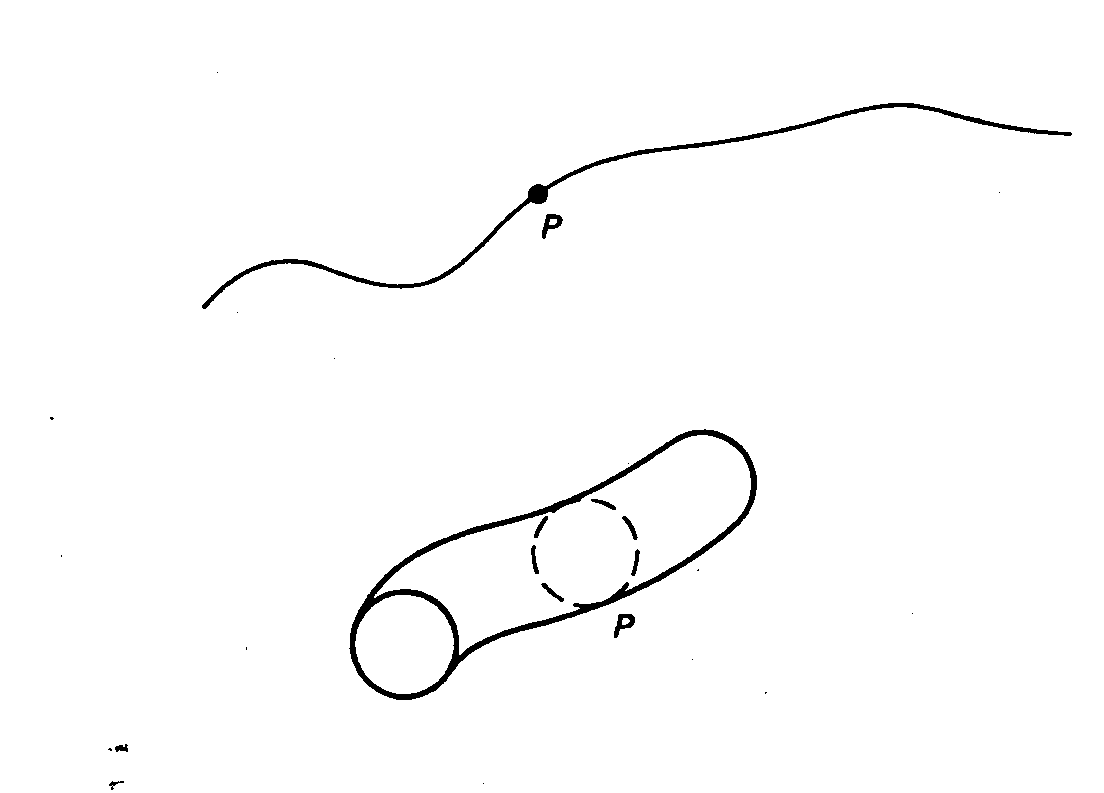
Figura 27. Desde una cierta distancia la manguera parece una línea sinuosa.
Una inspección desde más cerca nos revela que un punto P de la línea se con-
vierte en un circulo en torno a la circunferencia de la manguera. Es posible que lo
que normalmente tomamos por un punto en el espacio tridimensional sea en
realidad un pequeño circulo en torno a otra dimensión del espacio. Esta idea es
la base de la teoría unificada de Kaluza y Klein de las fuerzas electromagnéticas
y gravitatorias.
 

Klein consiguió calcular la circunferencia de los bucles en la quinta
dimensión a partir de los valores conocidos de la unidad de carga eléc-
trica de los electrones y otras partículas y de la intensidad de las fuerzas .
gravitatorias entre partículas. El valor resultó ser de 10^-32 cm, aproxi-
madamente 10^-20 veces el tamaño de un núcleo atómico. No es sor-
prendente que no hayamos observado la quinta dimensión, puesto que
se halla enrollada hasta alcanzar una magnitud mucho menor que cual-
quier estructura percibida hasta la fecha, incluso en la física de partícu-
las subnucleares. No es posible, pues, que un átomo se mueva en la
quinta dimensión. Más bien debemos pensar en la nueva dimensión
como algo que se halla dentro del átomo.

Pese a su ingeniosidad, la teoría de Kaluza-Klein fue poco más que
una curiosidad matemática durante más de cincuenta años. Con el
descubrimiento de las fuerzas débil y fuerte en la década de los 30, la
idea de unificar gravedad y electromagnetismo perdió mucho de su
atractivo. Cualquier teoría de campo unificado viable tendría que aco-
modarse no solamente a dos, sino a cuatro fuerzas. Este paso no pudo
realizarse, pues, hasta que se tuvo una comprensión adecuada de las
fuerzas débil y fuerte. A finales de los años 70, con las GTU y la super-
gravedad frescas en las mentes de los teóricos, alguien recordó la an-
tigua teoría de Kaluza-Klein. Rápidamente fue sacada de entre la nafta-
lina, desempolvada y remodelada para acomodarse al nuevo paquete
de fuerzas conocidas.

En las GTU, la capacidad de los teóricos de subsumir tres tipos muy
diferentes de fuerzas bajo un solo paraguas conceptual dio lugar, como
vimos en capítulos anteriores, al descubrimiento de que las tres fuerzas
implicadas pueden ser descritas en términos de campos de gauge. La
propiedad central de esos campos es la presencia de algunas simetrías
abstractas, hecho que les da su poder y elegancia. La presencia de
simetrías en los campos de fuerza sugiere intensamente algún tipo de
geometría oculta. En la teoría de Kaluza-Klein revitalizada, las simetrías
del campo de gauge se vuelven concretas; son las simetrías geomé-
tricas asociadas a las nuevas dimensiones espaciales.

Como en la versión original de la teoría, las fuerzas se acomodan
injertando más dimensiones espaciales en el espaciotiempo conocido,
pero el hecho de que ahora tengamos tres fuerzas que acomodar re-
quiere varias dimensiones adicionales. Un simple recuento del número
de operaciones de simetría necesarias para la gran fuerza unificada nos
lleva a una teoría en la cual debe haber siete nuevas dimensiones, su-
mando diez dimensiones espaciales en total, más el tiempo, o sea once
dimensiones espaciotemporales. La versión moderna de la teoría Kalu-
za-Klein postula un Universo de once dimensiones.

Una vez más, es necesario suponer que estas siete dimensiones
espaciales están "enrolladas" hasta alcanzar un tamaño muy pequeño,
de modo que no las percibimos. Sólo hay una forma de enrollar una
dimensión adicional, y es en un círculo. Los espacios de más dimen-
siones, sin embargo, pueden comprimirse de muy distintas formas. Por
ejemplo, una superficie bidimensional puede unirse por los extremos
para formar o bien la superficie de una esfera o bien la de un donut
(conocido como un toro). Aunque ambas estructuras son cerradas y
pueden hacerse muy pequeñas, difieren profundamente en su topo-
logía; el donut posee un agujero que lo atraviesa.

Con siete dimensiones, el número de topologias posibles es enor-
me. ¿Qué forma es la correcta? Una elección particularmente atractiva
es el análogo heptadimensional de la esfera, conocido simplemente
como heptaesfera. Si las dimensiones espaciales invisibles tienen real-
mente esta forma, entonces cada punto del espacio bidimensional es
de hecho una diminuta "hiperesfera" de siete dimensiones. La hepta-
esfera llamó la atención de los matemáticos hace más de medio siglo
debido a que posee unos rasgos peculiares que la dotan de interesan-
tes propiedades geométricas. No vamos a ocuparnos aquí de los deta-
lles, pero si la naturaleza tuviera que hallar una estructura geométrica
cerrada que permitiera las fuerzas y campos que percibimos en el mun-
do real, entonces la heptaesfera sería la elección más simple. Es impo-
sible obtener el tipo de estructuras que nos rodean, desde los átomos
hasta las galaxias, con una disposición matemática más simple.

Una esfera es una figura altamente simétrica, y una heptaesfera
posee muchas simetrías adicionales que no se encuentran en la esfera
corriente. Con ellas se pretende identificar las simetrías de gauge sub-
yacentes a los campos de fuerza. Sin embargo, una de las razones de
que los físicos tardaran tanto tiempo en descubrir las fuerzas es que las
simetrías se hallan a veces ocultas, e incluso interrumpidas, a la manera
descrita en el Capítulo 8. En la teoría de Kaluza-Klein, esta interrupción
de la simetría se consigue distorsionando la estructura heptadimen-
sional de forma que no sea una esfera exacta. La heptaesfera "acha-
tada" resulta ser la forma óptima en lo que respecta a las comprimidas
dimensiones invisibles.

La teoría de Kaluza-Klein resucitada ha sido tan inspiradora que los
físicos se han apresurado a reescribir las leyes de la física en once di-
mensiones. Un problema que surge de inmediato es comprender por
qué el espaciotiempo adopta esta escisión siete-cuatro. ¿Es inevitable
que siete de las once dimensiones se enrollen hasta hacerse invisibles,
dejando tras ellas las cuatro dimensiones de la experiencia directa? ¿O
existe alguna otra posible configuración distinta, digamos ocho-tres?

En su búsqueda de una razón por la cual siete de las dimensiones
deberían comprimirse espontáneamente, los teóricos han supuesto
que los sistemas físicos tienden siempre a buscar su estado más bajo de
energía. Vimos un buen ejemplo de este principio en el Capítulo 8, con
la esfera en el "sombrero mexicano": la esfera encuentra finalmente un
estado estable de la más baja energía en el "borde del sombrero". Qui-
zá una heptaesfera "achatada" es en cierto sentido la configuración de
menor energía del espaciotiempo.

Pero es concebible que la configuración de la heptaesfera sea tan
sólo una de las muchas disposiciones posibles. Es fascinante conjeturar
que muy lejos en el Cosmos, más allá de los límites de nuestro Univer-
so observable, el espacio posee otro número de dimensiones. Tras un
viaje de miles de millones de años luz, quizá nos descubriéramos de
pronto en un universo de cinco dimensiones espaciales en vez de tres.

De ser así, puede que tengamos una respuesta a la pregunta "¿Por qué
tres?" Es posible que el espaciotiempo de once dimensiones se organi-
ce a si mismo en dominios de distinta dimensionalidad aparente. Pues-
to que la estructura de los campos de fuerza depende de las simetrías
geométricas de las dimensiones comprimidas, esas fuerzas diferirán de
un dominio a otro. Junto a esas diferencias estarán los muchos proble-
mas sobre órbitas estables, movimiento ondulatorio, etc., discutidos
anteriormente. Todo ello asegurará que las condiciones físicas en los
dominios que no gozan de una escisión siete-tres sean muy distintas de
las de nuestro propio Cosmos. Es dudoso que la vida puede florecer, o
siquiera existir, en tales dominios. Los organismos vivos son altamente
delicados y parecen depender críticamente de la oportuna v única
colección de fuerzas reunidas en nuestra región del Universo. Esto
parece indicar que nosotros, como observadores, hemos seleccionado
con nuestra propia presencia una región de espaciotiempo con tres
dimensiones espaciales perceptibles. Simplemente, no podríamos vivir
en ninguno de los otros dominios dimensionalmente distintos que tal
vez existan.

¿POR QUÉ ONCE?

El uso de este razonamiento "antrópico" para explicar la tridimen-
sionalidad del espacio plantea otra intrigante pregunta. ¿Debe ser ine-
vitablemente once el número total de dimensiones espaciotemporales,
o puede variar de lugar a lugar? ¿Es posible un Universo de veintiuna
dimensiones, diecisiete de las cuales están comprimidas y dotan al
mundo de un esquema de campos de fuerza mucho más complejo que
el formado por los cuatro de nuestra experiencia? ¿Quién sabe qué
intrincadas estructuras, qué elaboradas formas de vida, pueden medrar
en un Universo así?

A lo largo de la historia, hombres y mujeres se han sentido fascina-
dos por la numerología. Los antiguos griegos daban a algunos números
un significado místico y metafísico. Hoy en día, el número cuatro -el
número de lados de un cuadrado- conserva aún un vestigio de su an-
tigua asociación con la honestidad y la justicia en la expresión inglesa
"a square deal", literalmente un trato cuadrado, para referirse a algo
hecho con honestidad y buena fe. Para mucha gente aún hay números
"de buena suerte" o "de mala suerte", como el tres, el siete o el trece.
La Biblia hace un uso repetido de los números siete y cuarenta. Toda-
vía se asocia el número 666 con el diablo.

Cuando los números se presentan de forma natural, es tentador
buscarles un significado oculto. A veces parecen ser puramente acci-
dentales, como con el número de planetas del sistema solar. Otros nú-
meros que se presentan de forma natural parecen tener un significado
más profundo. El número de hadrones resulta ser consecuencia del
número de permutaciones disponibles de combinaciones de quarks. La
dimensionalidad del espaciotiempo, ¿es tan sólo un accidente, como el
número de los planetas? ¿O es algo que esconde una verdad profunda
acerca de la estructura lógica y matemática del mundo físico?

Hay un curioso indicio de que el número once posee, de hecho, un
profundo significado matemático. Este indicio procede de una rama de
la física que, superficialmente al menos, no posee ninguna conexión
con la teoría de Kaluza-Klein; se trata de la supergravedad.

En el capítulo anterior discutimos la formulación más prometedora
de la supergravedad, conocida como N = 8. La críptica designación
"N = 8" necesita alguna explicación. La operación de supersimetría
relaciona partículas con distinto spin en una superfamilia de 163 par-
tículas. Podemos preguntarnos por qué hay solamente 163 partículas
en la superfamilia. Si la operación de supersimetría transforma una
partícula con un valor de spin en una partícula con otro, ¿por qué no
podemos seguir transformando y generar una interminable secuencia
de partículas de spin arbitrariamente grande? La respuesta es que, para
que la supersimetría sea propiamente una simetría, la familia tiene que
estar "cerrada" bajo las operaciones. Puede generarse tan sólo una
familia finita de partículas. Puesto que hay buenas razones matemáticas
por las que no pueden existir partículas con un spin mayor que 2, una
superfamilia con 163 miembros es la más numerosa posible.

La designación N = 8 hace referencia al número de posibles ope-
raciones de conexión entre partículas con distinto spin. Dado que la
dirección del spin puede apuntar tanto "arriba" como "abajo", su pro-
yección puede variar de +2 (una partícula de spin 2 que apunta hacia
arriba) a -2 (una partícula de spin 2 que apunta hacia abajo) en pasos
semienteros. Hay ocho de tales pasos entre -2 y +2, es decir, se necesi-
tan ocho operaciones de supersimetría para generar todas las proyec-
ciones de spin requeridas para edificar la superfamilia de partículas.
Este número está también relacionado con el número de especies de
gravitinos, ocho en esta teoría.

Tal como se formula normalmente, el concepto de spin hace refe-.
rencia a las propiedades de rotación de una partícula en el viejo es-
pacio tridimensional. Hace años, sin embargo, los matemáticos se
entretuvieron inventando descripciones de spin en espacios de otras
dimensiones con el fin exclusivo de ver lo que ocurría. Sucede que, en
lo tocante a la supergravedad, la teoría se simplifica si hay más de tres
dimensiones disponibles. De hecho, la descripción más simple se ob-
tiene con la versión de la teoría en once dimensiones. En once dimen-
siones, las ocho operaciones distintas de simetría de la supergravedad
N = 8 se reducen a una sola: se obtiene una supergravedad "N = 1".

Imaginemos a un matemático entusiasta que no tuviera conoci-
miento de la dimensionalidad del Universo real, pero que por razones
de elegancia y unidad descubriera la supergravedad. Se vería obligado
a formular una teoría en la que el espaciotiempo tuviera once dimen-
siones y llegaría a la conclusión de que, si la naturaleza sabe lo que
hace, once es el número de dimensiones del Universo real. ¿Es esta
concurrencia del número once un mero accidente, o indica una pro-
funda conexión entre supergravedad y la teoría de Kaluza-Klein? Mu-
chos físicos esperan que esta conexión sea real y que las dos tradicio-
nes de unificación en física -la supergravedad y las grandes teorías
unificadas- se amalgamen en una descripción común. Salam ha escrito
las siguientes palabras:

«Si esta teoría es correcta, puede que estemos muy cerca
de una unificación completa y definitiva de todas las fuerzas
en las que la materia y las cargas fundamentales son mani-
festaciones de dimensiones ocultas del espacio.»
 
 

LA GEOMETRIZACIÓN DE LA NATURALEZA

Hemos visto cómo el sueño de Einstein de obtener una teoría de
campo unificado a partir de la geometría está casi a punto de realizarse.
En la versión moderna de la teoría de Kaluza-Klein todas las fuerzas de
la naturaleza, no sólo la gravedad, son tratadas como manifestaciones
de la estructura del espaciotiempo. Lo que normalmente llamamos
gravedad es una curvatura en las cuatro dimensiones del espaciotiem-
po de nuestras percepciones, mientras que las otras fuerzas se reducen
a curvaturas espaciales de otras dimensiones. Todas las fuerzas de la
naturaleza no son más que geometría oculta en acción.

Hace mucho tiempo, en 1870, el matemático W. K. Clifford habló
a la prestigiosa Sociedad Filosófica de Cambridge "Sobre la teoría
espacial de la materia". Clifford declaró:

«Que las pequeñas porciones de espacio son como colinas en una superfi-
cie que por lo general es plana... Que la propiedad de ser curvado o distorsio-
nado se transmite constantemente de una porción del espacio a otra a la ma-
nera de una onda. Que esta variación de la curvatura del espacio es lo que
ocurre realmente en ese fenómeno que llamamos movimiento de la materia.
Que en el mundo físico no hay nada excepto esta variación.»

Esos pensamientos constituyen una profecía de la teoría general de
la relatividad, desarrollada casi medio siglo después por Einstein. Clif-
ford, sin embargo, parece ir más allá de la relatividad general al conje-
turar que, del mismo modo que las fuerzas, las partículas de materia no
son en si mismas más que protuberancias y repliegues de un espacio
vacío.

Sentimos una profunda compulsión a creer que el Universo entero,
incluida toda la materia aparentemente concreta que asalta nuestros
sentidos, es sólo un retozar de nada agitada, que en último término el
mundo no es más que una escultura de puro vacío, un vacío autoorga-
nizado. La geometría es la comadrona de la ciencia. El laborioso tra-
bajo de generaciones de astrónomos que cartografiaron las trayectorias
de los cuerpos celestes dio lugar a la revolución newtoniana y a la
explicación del movimiento celeste en términos de fuerzas y campos.

Ahora hemos dado un círculo completo: las fuerzas y campos se ex-
plican a sí mismos en términos de geometría.

A principios de los años 60, el físico teórico norteamericano John
Wheeler amplió el trabajo de Clifford y Einstein para construir una
teoría completa del mundo basada sólo en la geometría del espacio-
tiempo vacío. Llamó a su programa "geometrodinámica". Su objetivo
era la explicación tanto de las parficulas como de las fuerzas en tér-
minos de estructuras geométricas.

El modelo de Wheeler para la carga eléctrica proporciona una
buena ilustración de la filosofía que anima el proyecto. Según este
modelo, una partícula cargada es en realidad una especie de entrada o
portal a un pequeño túnel que comunica un punto del espacio con
otro, algo como un puente espacial en miniatura sobre otra dimensión.

El otro extremo del túnel lo veremos como otra partícula de carga eléc-
trica opuesta. Así, los dos extremos del "agujero de Wheeler" pueden ser
un par electrón-positrón, por ejemplo. Mientras que los científicos del
siglo XIX hubieran dicho que las "líneas de fuerza" eléctricas se concen-
tran y terminan en la partícula cargada, Wheeler dice que las líneas
simplemente se concentran a lo largo de ella para emerger intactas al
otro lado (fig. 28). De esta manera no hacen falta fuentes de electri-
cidad, sino tan sólo agujeros en el espacio para atrapar a los campos
eléctricos. -

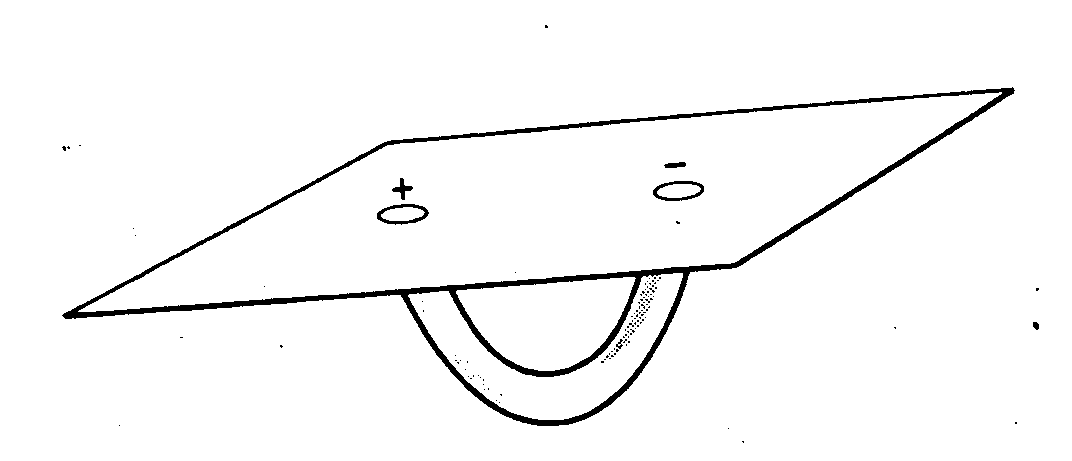
Figura 20. Wheeler conjeturó que una partícula cargada eléctricamente podía
ser el extremo de un pequeño tubo que pasa a través de otra dimensión y con-
cluye de nuevo en nuestro propio espacio tridimensional en el lugar de otra
partícula con carga opuesta.

La geometrodinámica tiene muchos encantos, pero nunca acabó
de funcionar. El propio Wheeler escribió que "el fallo más evidente...
es que no puede proporcionar un lugar natural al spin 1/2 en general y
al neutrino en particular". En años más recientes ha adoptado la pos-
tura de que cualquier teoría que asuma el espaciotiempo no puede
explicar también el espaciotiempo. En particular, la dimensionalidad
del espaciotiempo le es impuesta a la teoría desde el principio, y así no
puede obtenerse como una consecuencia de la teoría. Cualquier teoría
completa de la naturaleza debe dar razón de la existencia de la "materia
prima" -el propio espaciotiempo- que constituye el mundo geómetro-
dinámico. Wheeler cree que la única solución surgirá de un estudio de
la física cuántica y espera el día en que comprendamos que el cuanto,
más que el espaciotiempo, es el constituyente fundamental de la realidad.

Con la ventaja de la retrospectiva podemos ver que el fracaso de la
geometrodinámica de Wheeler se debe en parte a su restricción a cua-
tro dimensiones. Con once dimensiones, la variedad y complejidad de
las estructuras físicas que pueden construirse se amplía enormemente.

En la teoría de Kaluza-Klein, las partículas no son "agujeros" en el
espacio, sino excitaciones en una geometría de once dimensiones.
Esperemos que esta geometría pueda ser explicada, como el propio
Wheeler desearía, en términos del fenómeno cuántico.

LA EXPLORACIÓN DE LAS DIMENSIONES OCULTAS

Quizá la naturaleza sea hermosa, pero la sola belleza no conven-
cerá a los físicos de la corrección de una teoría. Se exige también la
prueba física. La potencia y la elegancia de la teoría de once dimen-
siones de Kaluza-Klein nos obliga a tomarla en serio, pero si no hay
ninguna forma concebible de verificar que las siete dimensiones adi-
cionales existen realmente, la teoría pierde mucho de su atractivo.

Afortunadamente, sin embargo, quizá sea posible demostrar Físi-
camente la existencia de las otras dimensiones. Para que la teoría fun-
cione, las siete dimensiones espaciales nuevas tienen que estar "enro-
lladas", probablemente en la forma de una heptaesfera, a una circunfe-
rencia de 10^-32 cm. Sondear estructuras a esta escala ultramicroscópica
es un reto importante: no poseemos control directo sobre ningún ob-
jeto tan pequeño, de modo que no podemos enviar nada "al interior"
de la heptaesfera para que la explore.

La física cuántica asocia una escala de energía (o su equivalente, la
masa) con una escala de longitud. Medida por medida, el diámetro de
un núcleo (aproximadamente 10^-12 cm) corresponde más o menos a la
masa del pión. A medida que sondeamos dimensiones mas pequeñas,
la energía necesaria empieza a aumentar. Para explorar el interior de
un protón hay que recurrir a energías al menos diez veces superiores a
la masa del protón. La masa de unificación se halla mucho más arriba
en la escala de energía, a aproximadamente 10¹⁴ veces la masa del
protón. Si pudiéramos disponer de una masa-energía tan enorme (y no
podemos), sería posible penetrar en el mundo de las partículas X, a
cuyo nivel la distinción entre quarks y leptones se desvanece.
¿Cuánta energía necesitamos para "penetrar" en la heptaesfera y
explorar las otras dimensiones del espacio? Según la teoría de Kaluza-
Klein es necesario ir mucho más allá de la escala de unificación, a una
energía equivalente a 10¹⁹ veces la masa del protón. Tan sólo a esta
energía inimaginable se manifestarán directamente las nuevas dimen-
siones.
El enorme valor de 10¹⁹ veces la masa del protón se conoce como
"escala de Planck", ya que fue descubierto originalmente por Max
Planck, el inventor de la teoría de los cuantos. A la energía de Planck,
las cuatro fuerzas de la naturaleza se fundirían en una sola superfuerza
y las diez dimensiones espaciales tendrían los mismos derechos. Si
pudiéramos concentrar la energía suficiente para ascender por encima
de la escala de Planck, la dimensionalidad del espacio quedaría ex-
puesta en todo su esplendor.

Demos rienda suelta a la imaginación y pensemos en el día en que
la humanidad controlará la superfuerza. Tendremos entonces la capa-
cidad de manipular el mayor poder del Universo, puesto que, en últi-
mo término, la superfuerza genera todas las fuerzas y todas las estruc-
turas físicas. Es el manantial de toda existencia. Con la superfuerza
liberada, podremos cambiar la estructura del espacio y del tiempo, atar
nuestros propios nudos en la nada, y dar orden a la materia. Controlar
la superfuerza nos permitirá crear y transformar partículas a voluntad,
generando exóticas formas de materia. Quizá seamos capaces de ma-
nipular la dimensionalidad del propio espacio, creando extraños mun-
dos artificiales con propiedades inimaginables. Con la superfuerza nos
convertiremos en los señores del Universo.

Pero ¿cómo puede conseguirse este control? En primer lugar, ne-
cesitamos dominar la energía suficiente. Para hacernos una idea de lo
que esto significa, comparemos: el acelerador lineal de Stanford tiene
3 km de largo y puede lanzar electrones a la energía equivalente a unas
veinte veces la masa del protón. Alcanzar la energía de Planck requeri-
ría un acelerador de longitud unas 10¹⁸ veces mayor, lo que lo haría
tan largo como la Vía Láctea... 100.000 años luz. ¡No es el tipo de
proyecto que pueda realizarse de la noche a la mañana!

En la teoría unificada de las fuerzas podemos distinguir tres umbra-
les cruciales o escalas de energía. El primero es la energía de Weinberg-
Salam, aproximadamente unas noventa masas de protón, más
allá de la cual las fuerzas electromagnética y débil se funden en una
sola fuerza electrodébil. El segundo es la energía de unificación, 10¹⁴
masas de protón, que marca el inicio de la física de la GTU. Finalmente
está la energía de Planck, 10¹⁹ masas de protón, que representa la
escala de energía a la que toda la física adquiere una espectacular sim-
plicidad. Uno de los grandes problemas abiertos es dar razón de estos
tres números y en particular explicar por qué el abismo entre el primero
y el segundo es tan enorme.

La tecnología actual solamente puede llevamos hasta el primero de
estos umbrales. Como vimos en el capítulo anterior, la desintegración
del protón nos puede proporcionar medios indirectos de sondear la
física a la escala de unificación, pero no parece haber ninguna esperan-
za en absoluto de obtener directamente la energía de unificación, y
mucho menos la energía de Planck.

¿Debemos concluir que nunca seremos capaces de observar direc-
tamente la acción de la superfuerza y percibir las siete dimensiones in-
visibles del espacio? Lo que sí es cierto es que, con el futuro Desertrón,
nos estamos acercando rápidamente al final del camino tecnológico.

Sin embargo, la tecnología humana no agota la totalidad de las circuns-
tancias físicas. Está la propia naturaleza. El Universo es un enorme
laboratorio natural donde hace 18.000 millones de años tuvo lugar el
más grande de los experimentos en física de partículas. Lo llamamos el
big bang. Veremos que esta dolencia primigenia consiguió desenca-
denar la superfuerza. Fue sólo un momento, pero quizá fue suficiente
para dejar una huella permanente de su antigua existencia.