I have been exploring some aspects of hysteresis analysis. A few
preliminary results of some simulation studies are presented here
for your comments/feedback. Later, I hope to have access to some
"real" data to further explore some of these ideas.
In a pharmacodynamic (PD)-pharmacokinetic (PK) context, hysteresis
is said to obtain when a plot of the drug effect, E, against
the corresponding plasma drug concentration (PDC) is multivalued,
i.e. a given PDC value corresponds to two or more E-values.
Figure 1 shows a typical hysteresis plot (HP) plot of miotic effect
versus PDC.
In this plot, in the region of maximum PDC, (at the right end),
E, continues to to increase, despite the essentially stationary
plasma values of about 17.5 units.
When effect, E, is observed to be a single valued function of
plasma drug concentration, a frequently used "Effect"
model is Hill's equation and its generalizations. We have:-
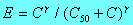
where E denotes the PD effect (on a zero to 1.00 scale),
and C denotes the corresponding PDC. The parameter, C50,
represents that value of the PDC for which E
= 0.5, while represents an arbitrary "shape" parameter
controlling the curvature of the E-PDC curve.
In the context of PD-PK analysis, equation (1) may be simply derived
using methods going back to Nernst, Langmuir, and others. Let
C be the concentration of drug in some phase (such as the plasma)
in contact with a surface containing N receptor sites, and let
effect E be directly proportional to the fraction of sites which
have formed drug-site complexes. Let denote the fraction (0 1.0)
of the N sites complexed with drug. We have:

and

where
At equilibrium
When such quasi equilibrium does not obtain the resulting HP will
be a "loop", rather than a single valued function.
To examine the non-equilibrium case we let
We have:-
with
and
as the differential equations connecting PDC and effect, E.
I put together several pieces of software to play with this. One
package (not presented here) takes "real" data and estimates
the rate constants (not a trivial task).on a subject - by - subject
basis for input to subsequent statistical analysis. Another routine
(in MS-DOS, and Windows 16 bit mode) simply takes a set of parameters
and plots the solution curves for Equations (2). The idea was
to get some idea of how the system looks.
Table 1 presents the 5 sets of parameter values chosen for exploration
of the behavior of this system.
*
Figures 2 (a&b) through 6 show plots of the solution curves.
If and when I get hold of real data I will try out the parameter
estimation process. Meanwhile your comments and criticisms would
be appreciated. If you want a no warranty, "as-is",
copy of the little routines I mentioned above, let me know by
email. You are welcome to the source code as well.
Thank you for visiting me!

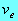


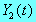
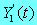

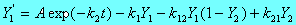
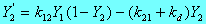




Case No. M* k1
k2 k12 k21
kd Case 1 25.00 0.100
0.200 0.100 0.050
0.020 Moderate Binding
Case 2 25.00 0.100
0.200 0.100 0.900
0.020 Loose Binding Case 3 25.00 0.100
0.050 0.100
0.050 0.020 Retarded absorption, Moderate Binding
Case 4 25.00 0.100
0.050 0.100
0.900 0.020 Retarded absorption, Loose Binding
Case 5 25.00 0.100
0.050 0.900
0.050 0.020 Retarded absorption, Strong Binding
Sign My Guestbook
View My Guestbook