The 47th Problem of Euclid
By Albert G. Mackey, 33º
Encyclopaedia of Freemasonry (1924)
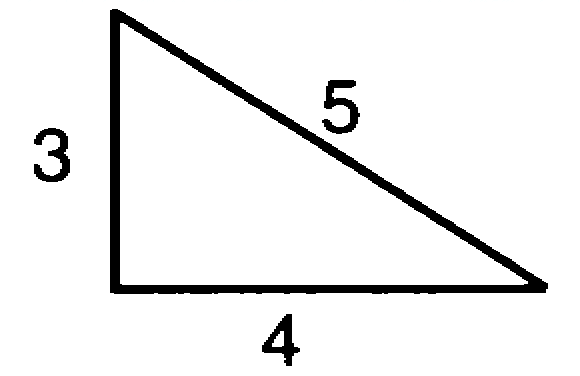
The forty-seventh problem of Euclid's first book, which has been adopted as a symbol in the Master's Degree, is thus enunciated: "In any right-angled triangle, the square which is described upon the side subtending the right angle is equal to the squares describedupon the sides which contain the right angle." Thus, in a triangle whose perpendicular is 3 feet, the square of which is 9, and whose base is 4 feet, the wquare of which is 16, the hypothenuse, or subtending side, will be 5 feet, the square of which will be 25, which is the sum of 9 and 16. This interesting problem, on account of its great utility in making calculations and drawing plans for buildings, is sometimes called the "Carpenter's Theorum."
For the demonstration of this problem the world is indebted to Pythagoras, who, it is said, was so elated after making the discovery, that he made an offering of a hecatomb, or a sacrifice of a hundred oxen, to the gods. The devotion to learning which this religious act indicated in the mind of the ancient philosophers has induced Masons to adopt the problem as a memento, instructing them to be lovers of the arts and sciences.
The triangle, whose base is 4 parts, whose perpendicular is 3, and whose hypothenuse is 5, and which would exactly serve for a demonstration of this problem, was, according to Plutarch, a symbol frequently employed by the Egyptian priests, and hence it is called by M. Jomard, in his Exposition du Système Métrique des Anciens Egyptiens, the Egyptian triangle. It was, with the Egyptians, the symbol of universal nature, the base representating Osiris, or the male principle; the perpendicular, Isis, or the female principle; and the hypothenuse, Horus, their son, or the produce of the two principles. They added that 3 was the first perfect odd number, that 4 was the square of 2, the first even number, and that 5 was the result of 3 and 2.
But the Egyptians made a still more important use of this triangle. It was the standard of all their measures of extent, and was applied by them to the building of the pyramids. The researches of M. Jomard, on the Egyptian system of measures, published in the maginificent work of the French savants on Egypt, has placed us completely in possession of the uses made by the Egyptians of this forty-seventh problem of Euclid, and of the triangle which formed the diagram by which it was demonstrated.
If we inscribe within a circle a triangle, whose perpendicular shall be 300 parts, whose base shall be 400 parts, and whose hypothenuse, and extend it through the bypothenuse to the circumference of the cirle, this chord or line will be equal to 480 parts, and the two segments of the hypothenuse, on each side of it will be found equal, respectively to, 180 and 320. From the point where this chord intersects the hypothenuse let another line fall perpendicularly to the shortest side of the triangle, and this line will be equal to 144 parts, while the shorter segment, formed by its junction with the perpendicular side of the tirnale, will be equal to 108 parts. Hence, we may derive the following measures from the diagram: 500, 480, 400, 320, 180, 144, and 108, and all these without the slightest fraction. Supposing, then, the 500 to be cubits, we have the measure of the base of the great pyramid of Memphis. In the 400 cubits of the base of the triangle we have the exact length of the Egyptian statium. The 320 gives us the exact number of the Egyptian cubits contained in the Hebrew and Baabylonian statium. The stadium of Ptolemy is represented by the 480 cubits, or length of the line falling from the right angle to the circumference of the circle, through the hypothenuse. The number 180, which expresses the smaller segment of the hypothenuse being doubled, will give 360 cubits, which will be the stadium of Cleomedes. By doubling the 144, the result will be 288 cubits, or the length of the stadium of Archimedes; and by doubling the 108, we produce 216 cubits or the precise value of the lesser Egyptian stadium. In this manner, we obtain from this triangle all the measures of length that were in use among the Egyptians; and since this triangle, whose sides are equal to 3, 4, and 5, was the very one that most naturally would be used in demonstrating the forty-seventh problem of Euclid; and since by these three sides the Egyptias symbolized Osiris, Isis, and Horus, or the two producers and the product, the very principle, expressed in symbolic language, which constitutes the terms of the problem as enunciated Pythagoras, that the sum of the squares of the two sides will produce the square of the third, we have no reason to doubt that the forty-seventh problem was well known to the Egyptian priests, and by them communicated to Pythagoras.
Dr. Lardner in his edition of Euclid, says: "Whether we consider the forty-seventh proposition with reference to the pecular and beautiful relation established in it, or to its innumerable uses in every department of mathematical science, or to its fertility in the consequences derivable from it, it must certianly be esteemed the most celebrated and important in the whole of the elements, if not in the whole range, of mathematical science. It is by the influence of this proposition, and that which establishes the similitude of equi-angular triangles (in the sixth book), that geometry has been brought under the dominion of algebra; and it is upon the same principles that the whole science of trigonometry is founded.
"The XXXIId and XLVIIth propositions are said to have been discovered by Pythagoras, and extraordinary accounts are given of his exultation upon his first perception of their truth. It is, however, supposed by some that Pythagoras acquired a knowledge of them in Egypt, and was the first to make them known in Greece."
[ EUCLID47 ] [ GEOCITIES ]
