MIDI: Fragmento del Preludio de "La Traviata" de G. Verdi (1813-1901)ALGUNAS
CURIOSIDADES SOBRE LAS CIFRAS DE LOS CUADRADOS PERFECTOS
Un
número es cuadrado perfecto si puede desarrollarse como producto de dos factores iguales.
1ª. Si los enteros 1, 2, 3, 4, 5, 6, 7, 8, 9 ..., se elevan al cuadrado,
0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196 ...
se observa la siguiente ley: La cifra de las unidades de estos cuadrados forman un periodo simétrico.
0, 1, 4, 9, 6, 5, 6, 9, 4, 1, 0
con cifras iguales con relación a 5 o a 0.
2ª. Las dos últimas cifras de los cuadrados consecutivos forman un periodo de 51 números,
00, 01, 04, 09, 16, .... 76, 25, 76, ...., 16, 09, 04, 01, 00
simétricos con relación a 25 o a 00
Esta observación se extiende indefinidamente. Las tres últimas cifras de los cuadrados perfectos consecutivos forman un periodo de 501 números. Las cuatro últimas, forman un periodo de 2501 números, etc.
3ª. Hay algunos cuadrados que están escritos con cifras todas diferentes. Ejemplos:
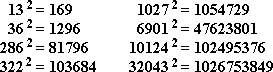
4ª. Los pares de cuadrados perfectos:
144 y 441, 169 y 961, 14884 y 48841
y sus respectivas raíces: 12 y 21, 13 y 31, 122 y 221, están formados por las mismas cifras, pero escritas en orden inverso.
El matemático Thébault investigó los pares que tienen esta curiosa propiedad. Encontró por ejemplo la siguiente pareja:
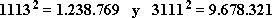
Volver a la página principal