ESTRELLA JOVEN - LA ESTRELLA DIGITAL |
EL CINICO |
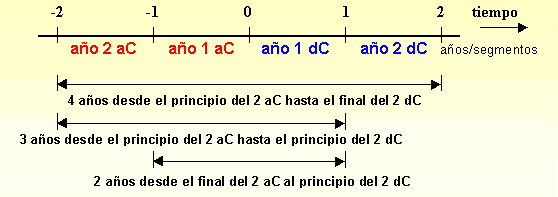
Sigue la polémica sobre el comienzo del siglo y del milenio, ante la complacencia de los grandes almacenes y los touroperadores, que tendrán la sabiduría de celebrarlo dos veces, el 2000 y el 2001, para regocijo de sus cajas. Ante todo lo que se viene diciendo y publicando, y en concreto ante lo que escribía la semana pasada Angel Riego, hay algunas cosas que decir: 1) El calendario actual se estableció sin año cero, comenzando en el año 1. Así pues, el siglo XXI y el tercer milenio de nuestro calendario comienzan el 1 de enero del 2001. Otra cosa es que este calendario sea erróneo y no cuente en realidad los años transcurridos desde el nacimiento de Jesús (que tampoco está muy claro que existiera realmente, y a la opinión de Bertrand Russell me remito), o que se prefiera otro calendario que contenga un "año cero" que haga que el cambio de siglo y milenio ocurra en el 2000, para que les quede la cosa bonita y esférica. 2) Al contrario de lo que se suele argumentar, no es cierto que sea necesario un año cero para calcular correctamente intervalos entre fechas. Basta con hacerlo bien. Es falso que entre el año 2 a.C. y el año 2 d.C. haya 3 años. En realidad, puede haber 4 o 3 o hasta 2: Desde el comienzo del año 2 a.C. hasta el final del año 2 d.C. hay exactamente 4 años; igualmente, sin ninguna contradicción, entre el final del año 2 a.C. y el comienzo del año 2 d.C. hay sólo 2 años; y entre el comienzo del 2 a.C. y el comienzo del 2 d.C. hay 3. Esto es así porque los años no son puntos, sino segmentos en la recta continua del tiempo, recta cuyo origen es el punto/instante cero, t=0, el primer instante del 1/1/1 d.C. de nuestro calendario.
El año 2 d.C. es el segmento [1,2] en la recta del tiempo, y el año 2 a.C. el segmento [—2,—1] (véase la perfecta simetría entre los dos segmentos). Para calcular intervalos de tiempo no podemos restar esos segmentos/años, tenemos que medir la distancia entre los puntos concretos de la recta continua del tiempo. Así, la frase "entre el año 2 a.C. y el 2 d.C. hay 3 años" , no es que sea o no correcta, es que está mal dicha, no tiene sentido, igual que no tiene sentido hablar de "la altura de arriba". Habría que decir: "Entre el instante t=—2 años y el instante t=2 años hay 2—(—2)=4 años". Esta es la solución correcta, o mejor dicho, la sintaxis correcta. De la misma manera, entre el 1/1/2 a.C. (t=—2) y el 1/1/2 d.C. (t=1) hay 3 años, y esto no entra en contradicción con la aritmética, porque no hay que restar los "nombres" de los años/segmentos: 2—(—2)=4, sino los instantes/puntos: 1—(—2)=3. Restar años/segmentos lleva además a una contradicción evidente: Pensemos en los años transcurridos entre las 0 horas del 1 de enero de 1999 y las 0 horas del 1 de enero del 2003 (las "0 horas" se refieren al primer instante/punto de cada uno de esos años, o sea, respectivamente, a los puntos t=1998 y t=2002, y por tanto esos "ceros" están bien utilizados). Restando los años/segmentos tendríamos 2003—1999= 4 años. Hasta aquí todo bien. Pero, ¿qué decir de los años transcurridos entre las 0 horas del 1 de enero de 1999 y las 24 horas del 31 de diciembre del 2002? ¿Decimos 2002—1999 = 3? Evidentemente no, ni siquiera redondeando o truncando, porque las 0 horas del 1/1/2003 y las 24 horas del 31/12/2002 son el mismo punto (t=2002) con dos nombres diferentes (los segmentos son intervalos cerrados y coinciden en un punto con el anterior y el siguiente). Con esto tendríamos dos resultados distintos para el mismo intervalo de tiempo, lo cual es absurdo. Así pues, para calcular intervalos de tiempo, los años/segmentos no se pueden restar como instantes/puntos, como números reales. Por tanto, la lógica que hace decir que entre el 2 a.C. y el 2 d.C. hay 3 años y que este "desatino" requiere la existencia de un año cero, es falsa, o, para hablar con propiedad, utiliza una mala sintaxis. Si se restan los instantes/puntos, como se debe hacer, no hay necesidad de ningún año/segmento cero. Basta con el instante/punto cero. Así, entre el instante t=0 (0 horas del 1/1/1) y el instante t=2000 (24 horas del 31/12/2000 o 0 horas del 1/1/2001) hay 2000—0=2000 años. Y entre el instante t=—1 (24 horas del 31/12/2 a.C. o 0 horas del 1/1/1 a.C.) y el t=2000, hay 2000—(—1)=2001 años. No hay ningún fallo aritmético. 3) En realidad, añadir un año/segmento llamado "cero" no variaría estos cálculos, puesto que ya hemos dicho que éstos se hacen con los puntos de la recta continua del tiempo (daría igual que los años se llamaran A,B,C... d.C. o a.C.). Se puede pensar, entonces, que sería deseable que, al calcular intervalos de tiempo entre fechas iguales de años/segmentos diferentes, el resultado coincidiera con la resta de los cardinales de esos años/segmentos. Si entre el 1 de enero de 1999 y el 1 de enero del 2003 hay 4 años, pero entre el 1 de enero del 2 a.C. y el 1 de enero del 2 d.C. no hay 4, sino 3, ¿por qué no ajustar este desfase añadiendo un año cero? Esto, que puede parecer que facilita las cosas, entra, sin embargo, en contradicción con el sentido común y plantea algunos otros problemas: Al ser los años segmentos discretos ordenados, o sea, elementos contables ordenados, lo lógico es designarlos con los números naturales. Nos los podemos imaginar como dos filas de lápices alineadas perpendicularmente a un lado y otro de una raya. Cada lápiz sería un año y, en este caso, hacia la derecha de la raya (el punto origen cero) los llamaríamos por su número seguido de la expresión d.C., y hacia la izquierda por su número seguido de la expresión a.C. Pero cero no es un número natural, y nunca se nos ocurriría llamar a uno de los lápices "lápiz número cero", ya que no existe el ordinal del cero (* ver nota). Diríamos "el lápiz número uno de la derecha" o "el lápiz número uno de la izquierda". Del mismo modo, tampoco tiene mucho sentido un año/segmento número cero. Siguiendo esta misma lógica, la matemática hace que las sucesiones de números reales tampoco tengan término cero. Igualmente, tampoco hay elemento químico de número atómico cero, porque los protones son también elementos contables discretos, como los años/segmentos. Hablar del año cero sería tanto como decir que el ombligo es el ombligo número cero de nuestro cuerpo, o que, contando desde el pulgar, el meñique es el dedo cuatro. Esta opinión se ve apoyada también en la evidente correspondencia entre la recta de los números reales y la recta continua del tiempo: En la recta de los números reales, el cero es el punto origen, y nunca podría llamarse cero a una unidad, o sea, a un segmento de longitud 1. De igual forma, en la recta del tiempo, el cero es un punto y no tiene sentido como segmento. Si en un partido de fútbol se marca un gol a los 30 segundos, el cronómetro (que indica un tiempo que podemos considerar "continuo" en la práctica, o sea, con saltos discretos muy pequeños, de centésimas de segundo) señalaría t=0'30". Este sería el punto/instante de la recta del tiempo. Tomando como unidad en este caso el minuto, el segmento en el que se encuentra ese instante t=0'30" sería el segmento primero desde el origen, el que engloba todos los instantes del intervalo [0, 1], esto es, el minuto de ordinal 1, el minuto 1. Además, no deja de resultar extraño que se pueda llegar a llamar "cero", "nada", a una cosa tan consistente y larga como 365 días y pico. No admitir el año cero no es cuestión de "escasa imaginación", sino de saberse contar los dedos, cosa que parece que para algunos no resulta tan fácil. 4) Supongamos que, a pesar de todo lo que hemos explicado, decidimos añadir un año cero. ¿Dónde lo situamos? Siguiendo la lógica del "cuentakilómetros" que defienden los partidarios del año cero, debería ser en el primer año de la Era Cristiana, o sea, el 1 d.C. El año cero comenzaría en el punto/instante t=0, las 0 horas de ese 1 de enero de la supuesta circuncisión de Jesús, y hasta un año después no comenzaría el año 1 d.C. Lo que ocurre es que, si el año 1 d.C. pasa a ser el 0, entonces, el año 2 d.C. pasaría a ser el 1 d.C. , y el actual 1999 sería el 1998. Por lo tanto, en el "nuevo calendario", ahora nos dispondríamos a entrar en el 1999, no en el 2000, y, de todas maneras, el próximo 1 de enero no se cambiaría ni de siglo ni de milenio. Como el objetivo es formar el cachondeíto en este 2000, muchos partidarios del año cero niegan su propia lógica, la del cuentakilómetros, y pretenden situar el año cero no en el 1 d.C., sino en el 1 a.C., para que no moleste a los vivos. Pero con el año 0 en el 1 a.C. y la lógica de los "años cumplidos", tendríamos la contradicción de que, al llegar al punto cero de la recta continua del tiempo, o sea, al "nacimiento simbólico" de Jesús, ya se cumpliría un año de la Era Cristiana (¡¡??). Además, el año de la supuesta circuncisión de Jesús seguiría siendo el 1 d.C., ¡exactamente igual que ahora! En cualquiera de estos dos casos, además, la distribución de los segmentos alrededor del punto origen t=0 rompería la simetría de los intervalos, condición deseable geométrica y hasta estéticamente. Con el año 0 en el 1 a.C. , p.ej., el año 2 d.C. sería el intervalo [1,2]; sin embargo, el 2 a.C. sería el [—3,—2] en vez del [—2,—1], como es ahora. Conclusiones: 1) El calendario actual es arbitrario, como todos, pero no incoherente. No supone ningún error ni ninguna desventaja no tener año cero. Es más, prescindir del "año cero" es lo más lógico apelando al sentido común y a los conceptos elementales de la matemática. 2) Añadir un año cero no sirve de nada porque no varía los cálculos entre fechas, que se deben hacer entre los puntos/instantes de la recta continua del tiempo, sea cual sea la nomenclatura para los años/segmentos. 3) El año cero rompería la simetría de los años/segmentos a un lado y otro del origen. 4) Cambiar el calendario actual supondría un innecesario trastoque de fechas. 5) De todas maneras, aun con un calendario empezando en el año cero, ni el siglo ni el milenio cambiarían el próximo 1 de enero, a menos que obviemos el contrasentido de que en el momento t=0 se cumpliese 1 año de la Era Cristiana. Esta última contradicción, además, nacería de una solución ad hoc totalmente gratuita e inadmisible. 6) Querer que el siglo y el milenio comiencen en el 2000 no tiene más fundamento que el regocijo de cambiar la cifra de las unidades de millar y, digámoslo así, la admiración que produce la redondez de los ceros. O sea, una pueril superstición numerológica y seudomágica que resulta primitiva y ridícula. Así, pues, "según la falsa cronología al uso" que decía Nietzsche, que es la que, para bien o para mal, utilizamos, el siglo XXI y el tercer milenio comienzan el 1 de enero del 2001. Este es el calendario que tenemos y no veo ninguna razón para cambiarlo, salvo que hayamos pagado un riñón para disfrutar "el fin del milenio" en una suite del Ritz de París, claro. Entonces, duele. P.S: Pido disculpas a mis lectores por el brutal cambio de estilo en este largo artículo. De vez en cuando, renace el hombre de ciencias que soy.
(*) Como caso curioso, Bruckner sí tiene una Sinfonía Nº 0, que denominó así por ser una obra de juventud poco madura, e incluso una Sinfonía 00, una especie de "protosinfonía". Es que él quería empezar a contar 1 con la primera que le gustara. (Volver al texto)
|