Quadratic Formula

The Quadratic Formula:

The quadratic is probably the second most famous formula in mathematics. Perhaps only the Pythagorean Theorem is more renowned. The quadratic formula is utilized to solve quadratic equations. That is equations of the form,

(Q)

a× x

b× x

aš

The derivation of the quadratic formula involves two ideas of mathematics. The most basic is the square root property, which tells us that when a variable squared is equal to a positive constant, the variable can be either the principal square root or the negative square root of the constant.

(S)

The other idea is really a much more complex methodology, called "completing the square." In this process we note that a quadratic equation a× x² + b× x + c = 0, aš 0, may always be written in a form to which the square root property may be applied. The process requires:

(Q)

c/a

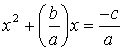
4.) The CST is then added to both sides of the equation.

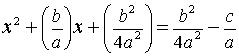
5.) Now note the left hand side of this equation is expressable as a perfect square binomial and the right hand side is expressable as a single rational expression. Thus an equivalent form for the above equation is:

6.) We have now completed the square and may apply the square root property to the above equation yielding:

7.) Now isolating the x variable on one side of the equation and distributing the square root over the quotient produces:

8.) Finally, using the common denominator, the solution is stated in its most common and famous form as

Now we may read the quadratic formula as "x equals negative b plus or minus the square root of the difference, b squared minus four a c, all over two a."