Para graficar en MatLab puedes teclear en el promp del programa

EDU>>

Las siguientes opciones de help:

Donde podrás revisar con más detalle las opciones de graficación.

En este documento te pondré los listados para generar las gráficas que se vieron en clase, estos listados los puedes generar con cualquier editor simple de texto como el Notepad.exe sólo que al final debes de salvarlo con la extensión .m, es decir en lugar de polin.txt debes salvarlo como polin.m de otra forma MatLab no lo va a reconocer, además debes de salvarlo dentro del folder de MatLab, por ejemplo en:

C:\MatLab\

y podrás ejecutarlo desde el promp de MatLab como si fuera un comando de MatLab, solo recuerda no ponerle a tus archivos nombres reservados como los de los propios comandos de MatLab, ejemplo:

EDU>>polin

Empezamos entonces:

Archivo pol1.m el listado es el siguiente:

--------------------------------------------------------------------

% Esta es una línea de comentario, no influye en la secuencia

%La siguiente línea delimita el límite inferior de -6 y el superior de 6

% con un incremento de 0.005, esta es la precisión de graficación

x = -6: 0.005 :6;

% Se define la función

y = x.^3-4*x.^2-25*x+100;

% Tipo de gráfica y opciones de graficación

plot(x, y,'w')

grid on

xlabel('x'); ylabel('f(x)')

---------------------------------------------------------------------

Cuando lo hayas generado y salvado en el folder de MatLab, cuando escribas en la ventana principal:

EDU>>pol1.m

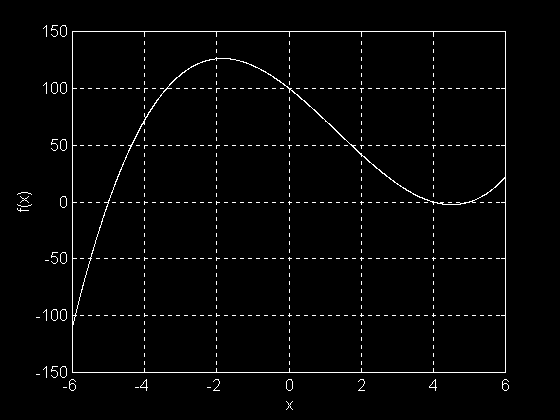
Se ejecuta lo siguiente, qué es la gráfica de la función polinomial

f(x) = x³ - 4x² - 25x + 100

Que tiene intersecciones en (-5, 0), (4, 0) y (5, 0):

Archivo pol2.m

Listado:

----------------------------------------------------------------------

x = -2.3: 0.005 :1.3;

y = x.^6+7*x.^3-8;

plot(x, y,'w')

grid on

xlabel('x'); ylabel('V(x)')

----------------------------------------------------------------------

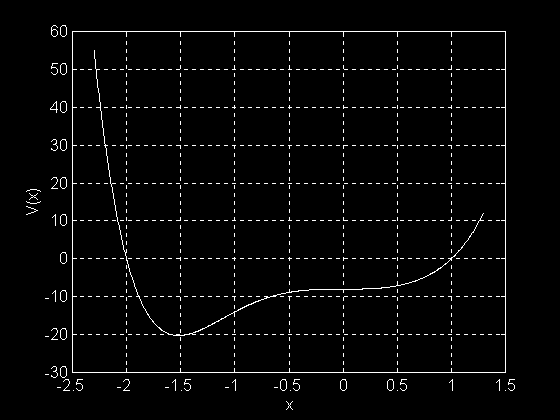
Esta es la gráfica de la función polinomial f(x) = x⁶ + 7x³ - 8

Que tiene cuatro soluciones complejas y dos reales, que representan los puntos de cruce de la función: (-2, 0) y (1, 0)

EDU>>pol2.m

Se ejecuta lo siguiente:

Archivo pol3.m

Listado:

----------------------------------------------------------------------

x = -0.5: 0.005 :8;

y = 4*x.^3-48*x.^2+144*x;

plot(x, y,'w')

grid on

xlabel('x'); ylabel('V(x)')

----------------------------------------------------------------------

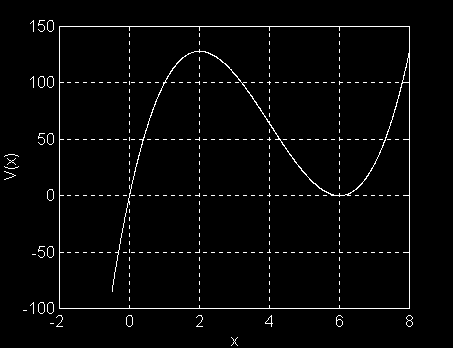
Esta es la gráfica de la función polinomial V(x) = 4x³ - 48x² + 144x

Esta función representa el comportamiento del volumen de una caja que depende de la longitud de x, el rango de interés es: (0, 0) y (6, 0)

EDU>>pol3.m

Se ejecuta lo siguiente:

Archivo pol4.m

Listado:

----------------------------------------------------------------------

x = -2.2: 0.005 :2.2;

y = x.^5-5*x.^3+4*x;

plot(x, y,'w')

grid on

xlabel('x'); ylabel('f(x)')

----------------------------------------------------------------------

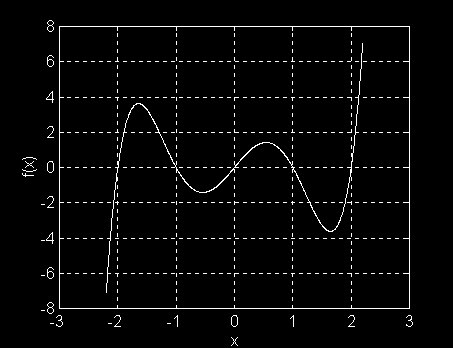
Esta es la gráfica de la función polinomial f(x) = x⁵ - 5x³ + 4x

Que tiene cinco soluciones reales, que representan los puntos de cruce de la función: (-2, 0), (-1, 0), (0, 0), (1, 0) y (2, 0)

EDU>>pol4.m

Se ejecuta lo siguiente:

Archivo pol5.m

Listado:

----------------------------------------------------------------------

x = -3.5: 0.005 :3.5;

y = x.^4-10*x.^2-2*x+4;

plot(x, y,'w')

grid on

xlabel('x'); ylabel('f(x)')

----------------------------------------------------------------------

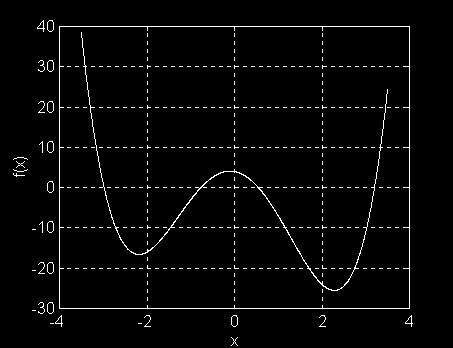
Esta es la gráfica de la función polinomial f(x) = x⁴ - 10x² - 2x + 4

Que tiene cuatro soluciones reales, que representan los puntos de cruce de la función, pero estas soluciones son números irracionales, que solo podemos aproximar, pero que ahí están.

EDU>>pol5.m

Se ejecuta lo siguiente: