IV-3- LOS NÚMEROS IRRACIONALES

3.- LOS NÚMEROS IRRACIONALES

Los pitagóricos, como hicimos notar, fueron los primeros en apreciar el concepto mismo de número y se propusieron emplear los números para describir los fenómenos fundamentales de los mundos físico y social. Para los pitagóricos, los números fueron también interesantes en sí mismos y por sí mismos. Les gustaron los números cuadráticos, es decir, números como 4, 9, 16, 25, 36, etc. y observaron que las sumas de ciertos números cuadráticos, o cuadrados perfectos, eran también números cuadráticos. Por ejemplo, 9 + 16 = 25, 25 + 144 = 169, y 36 + 64 = 100. También se pueden escribir así estas relaciones:

3² + 4² = 5², 5² + 12² = 13² y 6² + 8² = 10².

A los conjuntos de tres números cuyos cuadrados satisfacen igualdades como éstas se les sigue llamando hasta hoy tríos o ternas pitagóricas. Así, 3, 4, 5 constituyen una terna pitagórica porque 3² + 4² = 5².

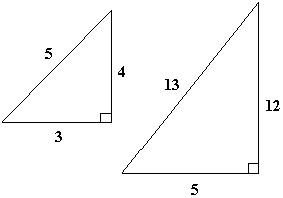
A los pitagoricos les gustaron mucho estas ternas porque, entre otros caracteres, ofrecían una interesante interpretación geométrica. Si los dos números más pequeños son las longitudes de los lados que forman el ángulo recto de un triángulo rectángulo, es decir, los catetos, entonces el tercer numero será la longitud de la hipotenusa (Figura 1). Es imposible precisar

Figura 1.

cómo establecieron los pitagóricos este hecho geométrico, pero aseguran que lo hicieron. Confirmaron también que en cualquier triángulo rectángulo el cuadrado de la longitud de un cateto agregado al cuadrado de la longitud del otro da el cuadrado de la longitud de la hipotenusa. A esta afirmación, de índole mas general, se le llama hasta hoy teorema de Pitágoras. Euclides, unos 200 años después que el maestro de Samos, dio la demostración de este teorema que aprendemos en el curso de geometría de la escuela secundaria (como la ven…). Se cuenta que Pitágoras se alegró tanto con este teorema, que mandó sacrificar un buey (es decir una res… nunca un alumno) para celebrar el descubrimiento.

Este teorema resulto ser la ruina de uno de los principios de la filosofía pitagórica y causo aflicción y desdicha a muchos matemáticos. Pero antes de proseguir la narración examinemos algunas propiedades simples de los números enteros que están implícitas en los siguientes ejercicios (si… si tienes que hacerlos… porque luego no vas a entender lo que sigue)

EJERCICIOS

1. Demuestra que el cuadrado de cualquier número par es par también [Sugerencia: por definición, todo numero par contiene 2 como factor.]

2. Demuestra que el cuadrado de cualquer numero impar es también impar [Sugerencia: todo numero impar termina en 1, 3, 5, 7 o 9.]

3. Sea a un numero entero. Demuestra que si a² es par, entonces a es par también. [Sugerencia: utiliza el resultado del ejercicio 2.]

4. Establece la verdad o la falsedad de la afirmación de que la suma de cualesquiera dos cuadrados es asimismo el cuadrado de un numero.

También en las matemáticas hay tragedias, y una de estas golpeó, a un grupo de matemáticos que merecía mejor suerte. Los pitagóricos edificaron una filosofía, para ellos mismos muy satisfactoria, en la que se aseguraba que todos los fenómenos naturales y los conceptos éticos y sociales eran, en esencia, más que números enteros o relaciones entre números enteros. Pero cierto día a uno de los miembros de la secta (siempre existe uno) se le ocurrió examinar el caso, al parecer más sencillo, del teorema de Pitágoras. Supongamos que cada uno de los catetos de un triángulo rectángulo (Figura 2) tiene una longitud de 1. ¿Cuál será entonces la longitud, se preguntó el curioso pitagórico, de la hipotenusa? E1 teorema de Pitágoras dice que el cuadrado (de la longitud) de la hipotenusa equivale a la suma de los cuadrados de los catetos. Por lo tanto, si llamaramos c a la longitud desconocida de la hipotenusa, de acuerdo con el teorema tendremos que

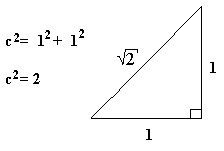
Figura 2.

Ahora bien, 2 no es un numero cuadrático, es decir, un cuadrado perfecto, y entonces c no es un numero entero. Pero a nuestro pitagórico le pareció desde luego razonable que c debería ser una fracción, es decir, que seguramente habría una fracción cuyo cuadrado fuera 2. La fracción 7/5 se acerca al valor correcto porque (7/5)² = 49/25, que es casi 2. Pero por muchas pruebas que se hagan no se encontrara la fracción cuyo cuadrado sea 2. Nuestro pitagórico empezó a preocuparse, y decidió investigar el asunto de sí existía o no existía una fracción cuyo cuadrado fuese 2. Examinaremos su razonamiento que, hasta donde sabemos, es el mismo que aparece en la famosa obra de geometría de Euclides, los Elementos.

Nos proponemos encontrar un numero c cuyo cuadrado sea 2. Lo representaremos con Ö 2. Este símbolo representa un numero cuyo cuadrado es 2. Supongamos ahora que Ö 2 es la fracción a/b, en donde a y b son números enteros. Además, para simplificar aún más el problema, supondremos que ya eliminamos todos los factores comunes de a y b. Por consiguiente, a/b fuera 8/6, por ejemplo, habríamos eliminado el factor común 2 y nos habríamos quedado con 4/3. Hasta aquí hemos supuesto que:

Ö 2 = b/a

(1)

y que a y b no tienen factores comunes.

De ser correcta la ecuación (1), entonces, elevando al cuadrado sus dos miembros, paso que se funda en el axioma de que números iguales multiplicados por números iguales dan resultados iguales (pues multiplicamos el miembro izquierdo por Ö 2 y el derecho por a/b), obtendremos

2 = a² / b²

Aplicando de nuevo el axioma de que números iguales multiplicados por números iguales producen resultados iguales, obtenemos el producto de ambos miembros de la ecuación por b²:

2b² = a²

(2)

El miembro izquierdo de esta ecuación es un numero par porque contiene 2 como factor. Por lo tanto, el miembro derecho deberá ser también un número par. Pero si a² es par, entonces, según los resultados del ejercicio 3, a deberá ser par también. Si a es par, deberá contener 2 como factor, esto es, a = 2d, en donde d es un numero entero. Sustituyendo este valor de a en (2) obtenemos

2b² = (2d)² = 2d × 2d = 4d².

(3)

Como

2b² = 4d²,

podemos dividir ambos miembros de esta ecuación entre 2 para obtener

b² = 2d².

(4)

Vemos ahora que b² es numero par y, naturalmente, recurriendo una vez más al resultado del ejercicio 3, b tendrá que ser igualmente numero par.

Lo que demuestra esta argumentación es que, si Ö 2 = a / b, entonces a y b deben, ser números pares. Pero desde el principio de nuestra argumentación eliminamos los factores comunes de estos números. Así todo, nos encontramos con que a y b siguen conteniendo 2 como factor común. Este resultado contradice el hecho de que a y b carecen de factores comunes. [Dicho de otro modo, a/b es una fracción irreductible.]

¿Por que desembocamos en esta contradicción? Como nuestro razonamiento es correcto, la única posibilidad estriba en que sea incorrecto el supuesto de que Ö 2 equivale a una fracción. En otras palabras, Ö 2 no puede ser la razón de dos números enteros.

Tan pulcra es esta demostración que casi se atreve uno a creer la conserja de que Pitágoras sacrifico un buey para celebrar esta creación. Pero hay por lo menos dos razones para creer que se trata de una patraña. Por principio de cuentas, de ser ciertos todos los cuentos que hablan de Pitágoras sacrificando un buey, es de pensarse que poco tiempo habrá tenido el geómetra para dedicarse a las matemáticas. En segundo lugar la demostración anterior fue todo menos un triunfo para los pitagóricos. El símbolo Ö 2 es un numero porque representa la longitud de una línea, a saber, la hipotenusa del triángulo de la figura 2. Pero este numero no es ni un entero ni una fracción. La filosofía pitagórica aseguraba que todo cuanto existe en el universo era reducible a números enteros. Ahora se patentizaba la insuficiencia de la doctrina. La existencia de números como Ö 2 fue amenaza tan seria para la filosofía pitagórica que, en otra leyenda, más creíble, se narra que los pitagóricos, que se hallaban en el mar en el momento del descubrimiento, arrojaron al agua a su autor, y juraron jamas revelar el hallazgo (macabro… no?).

Pero los secretos a la cara salen. Y los últimos griegos no tan solo sabían que Ö 2 no es ni numero entero ni fracción sino que también descubrieron que hay una colección indefinidamente grande de otros números que tampoco son ni enteros ni fracciones. Así, Ö 3, Ö 5, Ö 7 y, en general, la raíz cuadrada de cualquier numero que no sea cuadrado perfecto, la raíz cúbica de cualquier numero que no sea cubo perfecto, y así sucesivamente, son números que ni son enteros ni son fracciones. Él numero p , que es la razón de la circunferencia a su diámetro, tampoco es ni numero entero ni fraccionario. Todos estos "nuevos" números se llaman números irracionales. La palabra "irracional" significa ahora que estos números no pueden expresarse como razones de números enteros, pero en tiempos de los pitagóricos querían decir inmencionable, inescrutable o incognoscible.

Si estos números irracionales son en verdad tan comunes y representan longitudes de lados de triángulos y circunferencias de círculos en función de sus diámetros, ¿por qué no fueron descubiertos antes? ¿No se toparon con ellos ni los babilonios ni los egipcios? Sí supieron que existían; pero como sólo les interesaban los números que tuvieran aplicaciones inmediatas, utilizaron aproximaciones convenientes. Cuando se encontraban con la longitud Ö 2, se contentaban con asignarle valores como 1.4 o 1.41. Para p , como viste en una de las preguntas de la semana, utilizaban valores tan inexactos como 3.

Estos pueblos usaron tales aproximaciones, y nunca se dieron cuenta de que ni las fracciones ni los decimales más complicados jamás representarían con exactitud un número irracional. Egipcios y babilonios manejaron despreocupadamente los números irracionales y sus matemáticas. Tal vez los griegos fueron de casta intelectual muy diferente y no se contentaron con aproximaciones. Pero padecieron también cierta debilidad. Reconocieron que existían números que no eran ni enteros ni fraccionarios, pero tan convencidos estaban de que en el concepto de número no cabía nada más que enteros o fracciones, que no aceptaron que los irracionales fuesen números también. Y se limitaron a considerar estas cantidades como longitudes o como áreas geométricas. Por eso no desarrollaron nunca una aritmética de números irracionales. En su obra astronómica, por ejemplo no usaron mas que enteros y fracciones. Las dificultades que en este respecto experimentaron los griegos persiguieron a todos los matemáticos hasta los tiempos modernos. Los más grandes matemáticos se negaron a admitir que los irracionales eran números también y perpetuaron el procedimiento griego de tratar a esas cantidades como longitudes o áreas. Todos esos hombres desearon que los pitagóricos, en vez de haber arrojado por la borda al descubridor de tan incómodos números, hubieran arrojado a estos mismos.

Pero, a veces, debido a las necesidades de la sociedad, hasta los matemáticos tienen que soportar lo desagradable. En el siglo XVII, la ciencia empezó a desarrollarse a ritmo asombroso. Y la ciencia siempre necesita resultados cuantitativos. Acaso sea reconfortante saber que Ö 2 es cierta longitud, y que Ö 2 × Ö 3 es un área. Pero este conocimiento no basta cuando necesita uno resultados numéricos. A1 fin, los matemáticos tuvieron que aceptar el hecho de que, si se decidían a dar trato numérico a todas las cantidades que aparecieran en el quehacer científico, tendrían que empezar por manejar los irracionales también como números. La negativa de los matemáticos, que se prolongó por siglos, de conceder a los irracionales la categoría de números ilustra una de las facetas mis extrañas de la historia de las matemáticas: en este campo, igual que en la política, la religión y la economía, a veces no se aceptan las ideas nuevas.

La situación que debe enfrentarse, entonces, con toda entereza, es la de que hay otros números aparte de los enteros y los fraccionarios. Se entiende que estos últimos hayan sido creados y utilizados primero, pues se presentan en las situaciones físicas elementales con que se encuentra el hombre. Por otro lado, no es muy común encontrarse con los números irracionales. Sólo la aplicación de un teorema como el de Pitágoras nos hace percatarnos de su existencia, y aun así habrá que someterlos a demostraciones como la que se hizo en paginas anteriores para verificar que no son ni enteros ni fraccionarios. Y el hecho de que hayan entrado tarde en la escena matemática no los convierte en números menos aceptables o menos genuinos. Así como va incrementándose paulatinamente nuestro saber relativo a las variedades de seres humanos y animales que existen en el mundo físico, así también se ensancha nuestro conocimiento de las variedades de números y con criterio liberal aceptamos a estos extraños de igual manera que a los números con los que ya estamos familiarizados.

Pero, para poder utilizar los números irracionales debemos saber de qué manera operar con ellos, es decir, tenemos que aprender a sumarlos, restarlos, multiplicarlos y dividirlos. Ya vimos con los números enteros y los fraccionarios que, si deseamos que las operaciones que ejecutemos con ellos se adecuen a la experiencia, deberemos formular dichas operaciones de acuerdo con ésta. Lo mismo tenemos que hacer con los números irracionales. Podríamos definir como se nos antojara la adición, la multiplicación y las demás operaciones. Pero si queremos que estas representen situaciones físicas, deberemos definirlas atendiendo a éstas. Esto no es en realidad difícil. Como los números irracionales son cantidades, (cantidad se refiere a medida de algo, tiempo, fuerza, distancia, objetos en general. El número, en cambio, es tan sólo un concepto. Las operaciones matemáticas se definen y realizan con números, no con cantidades) lo mismo que los enteros y las fracciones, estos últimos pueden servirnos de guía para establecer las operaciones propias con aquellos. Bastará con unos cuantos ejemplos para entender los principios generales. ¿Será cierto que

Ö 2 + Ö 3 = Ö 5?

Para responder, consideremos la pregunta análoga de si es verdad que

Ö 4 + Ö 9 = Ö 13.

En el segundo caso está claro que 2 + 3 no es igual a Ö 13, pues Ö 13 es evidentemente menor que 4. Por lo tanto, no debemos sumar los radicandos, esto es, el 2 y el 3, de la ecuación anterior. ¿Y cuanto es entonces Ö 2 + Ö 3? Siendo números ambos sumandos, el total tendrá que ser también otro numero, sí, pero que no podrá escribirse de manera mas compacta que Ö 2 + Ö 3. Esta imposibilidad de combinar los sumandos no es nada nuevo ni problemático. Cuando sumamos 2 y 1/2, por ejemplo, la respuesta sigue siendo 2 + 1/2. Usualmente omitimos el signo de mas y escribimos 2 1/2, pero los sumandos en realidad no están combinados.

Veamos ahora si es cierto que

Ö 2 × Ö 3 = Ö 6.

Guiémonos de nuevo por lo que indique la operación análoga con números enteros. ¿Es verdad que

Ö 4 × Ö 9 = Ö 25?

Claro que sí lo es. Y así nos pondremos de acuerdo en que, para multiplicar raíces cuadradas, es suficiente con multiplicar los radicandos. Esto es

Ö 2 × Ö 3 = Ö 6.

También llegamos sin rodeos a las definiciones de las operaciones de substracción y división; Ö 3 - Ö 2 da lugar a un numero definido, pero la diferencia no puede escribirse de manera más sucinta que Ö 3 - Ö 2.

Para la división, digamos Ö 3 / Ö 2, el procedimiento, como en el caso de la multiplicación, se sugiere a sí mismo cuando observamos que

pues esta ecuación informa sencillamente que 3/2 = 3/2. Por tanto, estaremos de acuerdo en que

Estos ejemplos ilustran el principio general de que las operaciones con números irracionales se definen de modo tal que concuerden con las operaciones con números enteros cuando estos se expresan como raíces. Podríamos enunciar nuestras definiciones en forma general, pero no hay necesidad.

En aplicaciones concretas a menudo hacemos aproximaciones a números irracionales por medio de fracciones o decimales porque los objetos físicos reales no se pueden construir con exactitud de ninguna manera. Cuando tenemos que construir una longitud que estrictamente debiera ser de Ö 2, hacemos una aproximación a esta cifra. Como (1.4)² = 1.96, y este numero esta muy próximo a 2, 1.4 seria buena aproximación a Ö 2. Si deseáramos una aproximación mejor, determinaríamos hasta el centésimo más próximo el número cuyo cuadrado se aproximara a 2. Así, como

(1.41)² = 1.988 y (1.42)² = 2.016,

vemos que 1.41 es buena aproximación con dos decimales a Ö 2. Naturalmente, podríamos mejorar todavía mas la precisión de la aproximación. Pero lo que no debemos perder de vista es que, no importa cuantos decimales empleemos, nunca obtendremos el número que sea exactamente Ö 2, porque cualquier decimal con un numero finito de dígitos, o un número entero seguido de tal decimal, no es mas que otra manera de escribir una fracción, mientras que Ö 2, como ya se demostró concluyentemente, nunca podrá ser igual al cociente de dos números enteros.

El hecho de que a menudo hacemos aproximaciones a números irracionales cuando deseamos construir algo suscita la siguiente pregunta: ¿por qué no hacemos aproximaciones a los números irracionales siempre que estos aparezcan y nos olvidamos de las operaciones con los números irracionales como tales? Por ejemplo, para calcular Ö 2 × Ö 3, podríamos aproximarnos a Ö 2 con, digamos, 1.41, y a Ö 3 con 1.73, y luego multiplicar 1.41 por 1.73. El resultado es 2.44, y como (2.44)² es 5.95, vemos que es buena aproximación a Ö 6. Si quisiéramos una respuesta mas precisa, podríamos hacer aproximaciones más cercanas a Ö 2 y Ö 3 y luego multiplicarlas. Una de las razones de que en las matemáticas propiamente dichas no se hagan aproximaciones consiste en que estas son una ciencia exacta. Insisten en que los razonamientos tengan todo el rigor de que sean capaces los seres humanos.

El precio de tanto rigor es que tenemos que pensar más y esforzarnos más(a quién le dolió esto…). Luego veremos que las matemáticas han aportado tanto precisamente por su insistencia en la exactitud.

Hay también ventajas practicas en trabajar con los números irracionales tal cuales. Supongamos que tuviéramos que calcular (Ö 3)⁴, es decir, Ö 3 × Ö 3 × Ö 3 × Ö 3. La persona que insistiera en hacer aproximaciones calcularía Ö 3 con cierto numero de cifras decimales, por ejemplo, 1.732, y luego determinaría (1.732)⁴. Mientras que a la persona practica le llevaría una hora calcular y verificar sus cálculos, el matemático vería de inmediato que

Ö 3 × Ö 3 × Ö 3 × Ö 3 = (Ö 3 × Ö 3) (Ö 3 × Ö 3) = 3 × 3 = 9,

y emplearía el resto en dormir una siesta restauradora. Además, la respuesta del matemático es exacta, mientras que la del hombre practico no es exacta ni siquiera hasta los cuatro lugares decimales con que inició sus cálculos, ya que el producto de dos números aproximados es menos preciso que cualquiera de los factores. Para dar una respuesta precisa hasta el cuarto lugar decimal, el hombre practico tendría que haber hecho primero una aproximación de Ö 3 con siete decimales y luego hacer las multiplicaciones.

E1 numero irracional es la primera de muchas ideas sutiles que el matemático ha introducido para reflexionar en ellas y tratar con el mundo real. El matemático crea estos conceptos, idea maneras de trabajar con ellos de modo que se adapten a situaciones reales, y luego utiliza sus abstracciones para razonar sobre los fenómenos a los que se apliquen sus ideas.

EJERCICIOS

1. Expresa las soluciones a estos problemas de la manera más concisa que puedas:

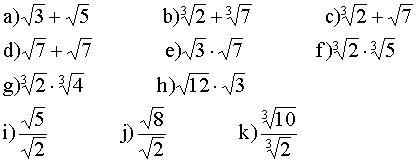
2. Simplifica las siguientes expresiones:

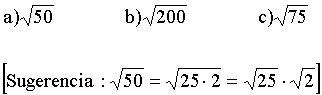
3. Analiza el siguiente razonamiento: no hay número irracional que pueda expresarse como decimal con un número finito de cifras. El número 1/3 no puede expresarse como decimal con un número finito de cifras. Por consiguiente, 1/3 es número irracional.

[Página principal] [Página anterior]