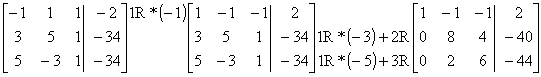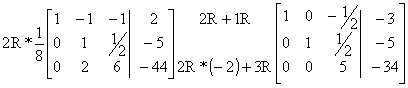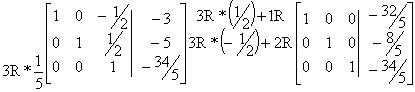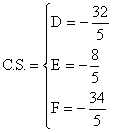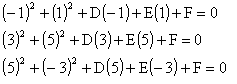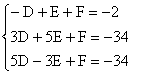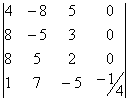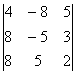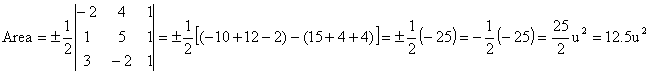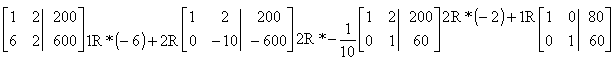Instituto Oriente
Matemáticas III, Examen Unidad I
Esta es una solución que contiene preguntas hechas en los exámenes de los grupos C, D y E.
- Encuentra la ecuación del círculo: x2 + y2 + Dx + Ey + F = 0, que pasa por los puntos (-1, 1), (3, 5), (5, -3). Plantea un sistema de 3x3 y resuélvelo por medio del procedo de eliminación gaussiana, llegando a un sistema escalonado reducido equivalente. (30 pts.)
Solución:
Se substituye cada punto en la ecuación general del círculo, que origina tres ecuaciones lineales con tres incógnitas:
|
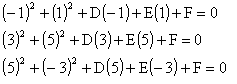
|
Þ |
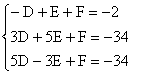
|
Al resolverlas utilizando las operaciones fundamentales de renglón, tenemos:
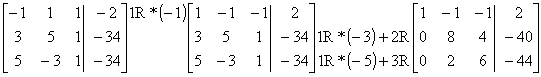
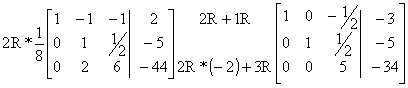
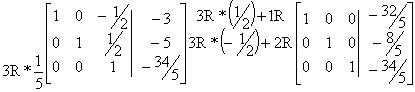
La solución de este sistema es entonces:
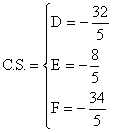
|
Que al substituirse en la ecuación del círculo obtenemos: |
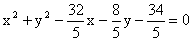
|
En su forma simplificada: 5x2 + 5y2 - 32x - 8y - 34 = 0
- Encuentra el determinante. (30 pts.)
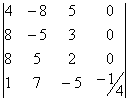
Solución:
Para obtener este determinante aplicamos el método de Menores, ya que es una matriz de 4x4 y no existe otro método:
Seleccionamos la columna o renglón que contenga el mayor número de ceros para que no tengamos que calcular tantos cofactores, así que seleccionamos la cuarta columna:
Determinante = C1,4 + C2,4 + C3,4 + C4,4 = 0 + 0 + 0 + (-1/4)(-1)4+4 * M4,4
Obteniendo el menor de la posición 4, 4 por el método de Sarrus:
|
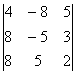
|
= (-40 - 192 + 200) - (-200 + 60 - 128) = 236 |
Obtenemos el determinante: (-1/4)(-1)4+4 * M4,4 = (- 1/4)(+1)(236) = - 59
- Utiliza el determinante para hallar el área del triángulo con vértices (
- 2, 4), (1, 5), (3, - 2). Gráfica el triángulo. (20 pts.)
Solución:
Se plantea el determinante que calcula el área de este triángulo:
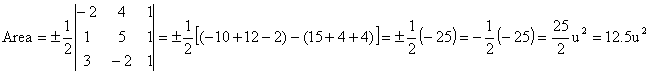
- En un experimento, los animales deben someterse a una dieta rigurosa. Cada animal consume, entre otros nutrientes, 20 gramos de proteínas y 6 gramos de carbohidratos. El investigador a cargo sólo dispone de dos mezclas alimentarias con las siguientes composiciones:
|
|
Proteínas (%) |
Carbohidratos (%) |
|
Mezcla A |
10 |
6 |
|
Mezcla B |
20 |
2 |
¿Cuántos gramos de cada mezcla debe utilizar para obtener la dieta correcta de cada animal? Plantea un sistema de ecuaciones lineales que modele este problema y resuélvelo por el método numérico de tu elección. (20 pts.)
Solución:
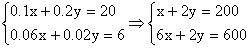
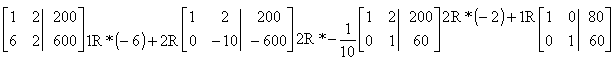
Entonces siendo x la cantidad de la mezcla A necesita ponerle 80 grs. y siendo y la cantidad de la mezcla B necesita ponerla entonces 60 grs. para cumplir las proporciones iniciales.

Página principal | Página anterior |