Instituto Oriente
Matemáticas III, Examen Unidad III
Esta es una recopilación de preguntas:
1) Si sabes que uno de los ceros de la siguiente función es 1 + 3i, encuentra todos los ceros restantes:
f(x) = x4 - 3x3 + 6x2 + 2x - 60
Desarrolla:
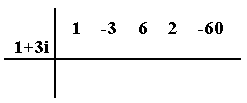
Solución:
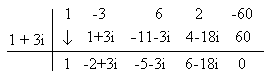
Como los coeficientes del polinomio de la función son todos números reales, sabemos que sus soluciones complejas son conjugadas, de ahí entonces probamos con otra solución:
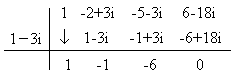
El último cociente corresponde a una expresión de segundo grado: (x2 - x - 6) = (x - 3)(x + 2)
Por lo tanto los ceros de la función son:
x1 = 1 + 3i; x2 = 1 - 3i; x3 = 3; x4 = -2
2) Encuentra todas las soluciones de la siguiente función y esboza una gráfica de la misma:
f(x) = 3x5 - 10x4 - 6x3 + 24x2 + 11x - 6
Solución:
Encontramos los candidatos a soluciones racionales según el teorema del cero racional:
![]()
Probando cada candidato en la división sintética:
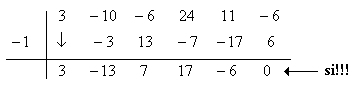
Lo que nos lleva a la factorización: 3x5 - 10x4 - 6x3 + 24x2 + 11x - 6 = (x + 1)(3x4 -13x3 + 7x2 + 17x - 6)
Para el siguiente factor aplicamos el mismo procedimiento de factorización:
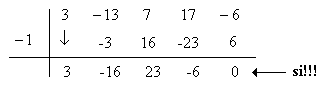
3x5 - 10x4 - 6x3 + 24x2 + 11x - 6 = (x + 1)(3x4 -13x3 + 7x2 + 17x - 6) = (x + 1)(x + 1)(3x3 - 16x2 + 23x - 6)
Y nuevamente:
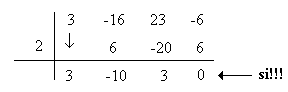
3x5 - 10x4 - 6x3 + 24x2 + 11x - 6 = (x + 1)(3x4 -13x3 + 7x2 + 17x - 6) = (x + 1)(x + 1)(3x3 - 16x2 + 23x - 6)
= (x + 1)(x + 1)(x - 2)(3x2 - 10x + 3) = (x + 1)(x + 1)(x - 2)(x - 3)(3x - 1)
Igualando la expresión completamente factorizada a cero:
(x + 1)(x + 1)(x - 2)(x - 3)(3x - 1) = 0
Obtenemos las soluciones o puntos de cruce de la función original:
x1 = -1; x2 = -1; x3 = 2; x4 = 3; x5 = 1/3
Por la prueba del coeficiente principal, sabemos que esta función va a caer a la izquierda y elevarse a la derecha, la gráfica exacta se muestra a continuación:
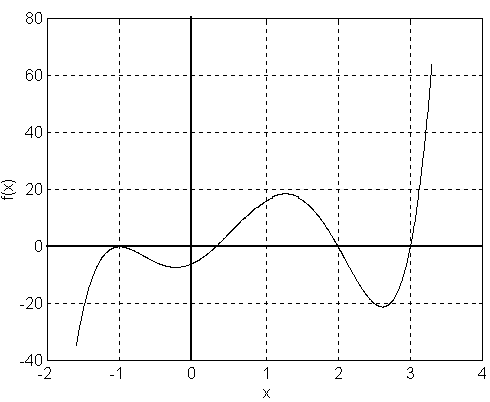
3) Usa la regla de los signos de Descartes para determinar el número de soluciones posibles y las combinaciones en que se podrían presentar: (no intentes resolverla)
f(x) = 6x4 - 25x5 + 14x2 + 27x - 18
Solución:
Primero debemos ordenar el polinomio: f(x) = - 25x5 + 6x4 + 14x2 + 27x - 18
Analizamos los cambios de signos para f(x) y determinamos el numero de soluciones posibles reales positivas.
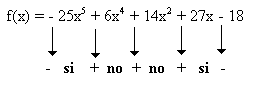
Puede tener 2 soluciones reales positivas o ninguna.
Analizamos los cambios de signos para f(- x) = 25x5 + 6x4 + 14x2 - 27x - 18 y determinamos el numero de soluciones posibles reales negativas.
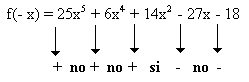
Tiene 1 solución real negativa.
Como sabemos que la función polinomial es de quinto grado, debe de tener cinco soluciones entre reales e imaginarias… así que las combinaciones posibles son:
|
Soluciones Reales + |
2 |
0 |
|
Soluciones Reales - |
1 |
1 |
|
Soluciones Complejas |
2 |
4 |
|
Total de Soluciones |
5 |
5 |
4) La concentración de cierto elemento químico en el torrente sanguíneo, t horas después de aplicarse una inyección en el tejido muscular, está dada por:
![]()
La concentración es mayor cuando 3t4 + 2t3 - 300t - 50 = 0. Aproxima este tiempo al décimo de hora más cercano.
Solución:
|
Iteraciones |
a |
c |
b |
f(a) |
f(c) |
f(b) |
Error |
|
1 |
4.000 |
4.500 |
5.000 |
-354 |
12.438 |
575 |
0.5 |
|
2 |
4.000 |
4.250 |
4.500 |
-354 |
-192.707 |
12.438 |
0.25 |
|
3 |
4.250 |
4.375 |
4.500 |
-192.707 |
-95.929 |
12.438 |
0.125 |
|
4 |
4.375 |
4.438 |
4.500 |
-95.929 |
-43.234 |
12.438 |
0.063 |
|
5 |
4.438 |
4.469 |
4.500 |
-43.234 |
-15.776 |
12.438 |
0.031 |
|
6 |
4.469 |
4.484 |
4.500 |
-15.776 |
-1.764 |
12.438 |
0.016 |
El cero es aproximadamente 4.484 con un error máximo de 0.016, Nos piden aproximarlo a décimos, por lo que tomamos entonces el valor de 4.5 y lo substituimos para encontrar la concentración del químico:
![]()
Por lo tanto la mayor concentración del elemento químico va a ser del 46% y se va a dar a las 4 horas y media después de aplicarse.
5) Demuestra que la siguiente ecuación no tiene ceros racionales:
x5 - 3x3 + 4x2 + x - 2 = 0
Solución:
Encontramos los candidatos a soluciones racionales según el teorema del cero racional y si ninguna de estas produce un residuo cero, entonces el polinomio no tiene soluciones racionales:
![]()
Probando cada candidato en la división sintética:
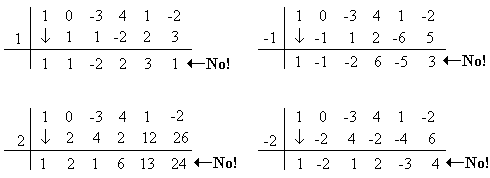
6) El costo C de pedir y transportar los componentes usados en la fabricación de cierto producto está dado por:
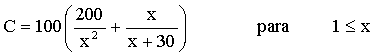
En donde C se mide en miles de dólares, y x es la cantidad del pedido en cientos de piezas. El costo es mínimo cuando 3x3 - 40x2 - 2400x - 36,000 = 0. Aproxima la cantidad óptima del pedido al centenar de unidades más cercano.
Solución:
|
Iteraciones |
a |
c |
b |
f(a) |
f(c) |
f(b) |
Error |
|
1 |
30.00 |
45 |
60.00 |
-63000 |
48375 |
324000 |
15 |
|
2 |
30 |
37.5 |
45 |
-63000 |
-24046.88 |
48375 |
7.5 |
|
3 |
37.5 |
41.25 |
45 |
-24046.88 |
7505.86 |
48375 |
3.75 |
|
4 |
37.5 |
39.38 |
41.25 |
-24046.88 |
-9375.72 |
7505.86 |
1.88 |
|
5 |
39.38 |
40.31 |
41.25 |
-9375.72 |
-1218.66 |
7505.86 |
0.94 |
El cero es aproximadamente 40.31 con un error máximo de 0.94, como x está en cientos de piezas, 40.31 serían 4031 piezas... y como nos piden aproximar este valor a centenas... entonces tomamos el valor de x = 4000 lo redondeamos a centenas x = 40 y encontramos el valor de C:
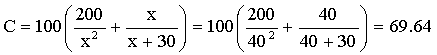
El costo mínimo se va a dar al transportar aproximadamente 4000 piezas y este costo será aproximadamente de $69,640.00 dólares.
![]()