Notas didáticas sobre o modelo de insumo-produto

Fernando Maccari Lara

 

Estas notas pretendem apresentar alguns conceitos básicos relativos à abordagem clássica do excedente a partir do modelo contábil-analítico que estrutura as matrizes de insumo produto. A despeito do domínio da abordagem neoclássica/ortodoxa no campo acadêmico, ainda sobrevivem análises de cunho clássico bastante úteis para a compreensão das condições e mudanças estruturais relativas aos sistemas econômicos capitalistas. Tem havido também um considerável esforço no âmbito da contabilidade social, para a construção de matrizes de insumo-produto nacionais e regionais. Diante disso, parece útil discutir algumas das conexões teóricas do modelo de insumo-produto, para assim contribuir para o melhor aproveitamento do material empírico disponível.

Discute-se dois tópicos: (a) demanda enquanto determinante da produção e do emprego (modelo de Leontief aberto em termos de quantidades); (b) preços de produção e a teoria do valor-trabalho (o modelo de preços de produção ).

Para isso, começaremos desdobrando o modelo usual de insumo-produto, em termos de valores monetários, em preços e quantidades.

Usualmente, as estimativas e análises de insumo-produto são realizadas sob o ponto de vista dos valores. Isso significa que a unidade básica de raciocínio do modelo são valores monetários que representam agregados de mercadorias, isto é:

 

 

onde P são preços e Q quantidades das N mercadorias envolvidas no modelo.

Neste sentido, todos os valores monetários representados em uma matriz de insumo-produto representam um produto entre preços e quantidades.

 

	I	II	III	DF	VBP
I	A11	A12	A13	DF1	VBP1
II	A21	A22	A23	DF2	VBP2
III	A31	A32	A33	DF3	VBP3
VA	VA1	VA2	VA3	PIB
VBP	VBP1	VBP2	VBP3		VBP

 

O quadro acima constitui o esquema contábil de um modelo do tipo Leontief aberto com três setores. As colunas representam o valor bruto da produção de cada setor desagregado em termos dos custos com insumos adquiridos dos outros setores e o valor adicionado, enquanto as linhas apresentam o valor bruto da produção decomposto em termos do destino, ou seja, enquanto parcelas da produção destinadas à demanda intermediária dos diferentes setores e à demanda final. A soma dos valores adicionados e a soma das demandas finais constituem o PIB.

De acordo com a observação que fizemos acima sobre os valores, nada estaríamos mudando no sentido desse esquema reescrevendo-o da seguinte forma.

 

	I	II	III	DF	VBP
I	Q11P1	Q12P1	Q13P1	QDF1P1	Q1P1
II	Q21P2	Q22P2	Q23P2	QDF2P2	Q2P2
III	Q31P3	Q32P3	Q33P3	QDF3P3	Q3P3
VA	VA1	VA2	VA3	PIB
VBP	Q1P1	Q2P2	Q3P3		VBP

Em termos das equações, a soma das linhas corresponde a:

 

 

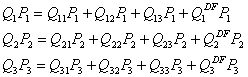
Onde Q1, Q2, Q3 representam as quantidades totais produzidas pelos três setores, enquanto P1, P2, P3 representam os preços das mercadorias produzidas pelos três setores. O produto do preço com a quantidade de cada setor corresponde ao seu valor bruto da produção. Q1DF, Q2DF, Q3DF correspondem às demandas finais de cada setor, em termos de quantidades. Multiplicadas pelos respectivos preços, correspondem ao valor da demanda final de cada setor. Q11, Q21, Q31 são as quantidades de insumos adquiridas pelo setor I, Q12, Q22, Q32 são as quantidades de insumos adquiridas pelo setor II, Q13, Q23, Q33 são as quantidades de insumos adquiridas pelo setor III. Da mesma forma, multiplicando essas quantidades pelo respectivo preço, obtém-se o valor das transações intermediárias.

Observe-se a respeito disso que Q11P1+Q12P1+Q13P1 representa a parte do valor da produção do setor I que foi utilizada como insumo na produção. Somando este agregado a Q1DFP1 obtém-se o valor bruto da produção total deste setor. É fundamental perceber porém que, desagregado dessa forma, as quatro parcelas referidas do valor bruto da produção representam o valor referente a quantidades de uma mesma mercadoria, qual seja aquela produzida pelo setor I.

Característica muito diferente, por outro lado, possui o agregado Q11P1+Q21P2+Q31P3. Ele representa o valor dos custos do setor I com a compra de insumos. Somado ao valor adicionado pelo setor também totaliza o valor bruto da produção do setor I. Diferentemente da desagregação citada acima, porém, o valor bruto da produção aparece como composto de mercadorias heterogêneas, ou seja é uma soma de valores que correspondem a quantidades de mercadorias produzidas por setores diferentes.

Estas considerações são fundamentais porque demonstram a diferença que existe quando analisamos o quadro de insumo-produto desdobrado em preços e quantidades no sentido das linhas e no sentido das colunas. No sentido das linhas os valores referem-se a diferentes quantidades de uma mesma mercadoria, razão pela qual só um preço aparece em cada linha.

 

O modelo de quantidades

 

Dividindo cada linha pelo respectivo preço, temos:

 

 

Definindo os coeficientes técnicos de insumo-produto como razão entre quantidades, teríamos:

Esta razão indica quantas unidades da mercadoria i são necessárias para produzir uma unidade da mercadoria j. Isto permite representar o sistema como:

 

 

Cuja solução, em forma matricial, seria

 

 

onde é a matriz de Leontief associada à matriz A dos coeficientes técnicos, Q é o vetor de quantidades totais produzidas pelos diferentes setores e QDF é o vetor de quantidades destinadas à demanda final. Este resultado é amplamente conhecido, porque exaustivamente utilizado no âmbito da programação econômica, e por isso apresentado na maioria das publicações didáticas sobre o tema. Dentre outras aplicações está a realização de estimativas de produção setorial a partir de alterações no tamanho e na composição da demanda final, para dadas condições técnicas de produção.

Outra possibilidade interessante a partir dessa formulação é a realização de estimativas de demanda de trabalho, quando associada a um vetor de coeficientes técnicos de trabalho direto L.

 

 

onde

 

Nesses termos. podemos definir a demanda total de trabalho como o produto entre o vetor L e o vetor Q, associado a determinada demanda final QDF e a uma matriz de coeficientes técnicos A.

 

 

Esta é uma definição formal interessante para a determinação do nível de emprego pela demanda efetiva. Dadas as condições técnicas de produção e o vetor de demanda final, determina-se o tamanho e a composição da produção, bem como o nível de emprego requerido.

Parece clara, portanto, a utilidade do modelo de insumo-produto para análises em termos de quantidades. Dada a estrutura de preços relativos, a demanda efetiva e as condições técnicas de produção aparecem como determinantes das quantidades produzidas e das quantidades de trabalho requeridas para tal produção.

 

O modelo de preços

 

Passemos agora ao problema dos preços. Veremos que o modelo também é muito útil, porém precisa ser observado do ponto de vista da desagregação no sentido das colunas, ou seja, em termos dos custos com insumos e o valor adicionado. Em termos das equações, teremos:

 

 

No modelo de quantidades dividíamos cada linha pelo respectivo preço, visto que os agregados eram compostos por quantidades diferentes da mesma mercadoria. Neste caso isto não é possível, porque o valor bruto da produção de cada setor está decomposto em valores relativos a quantidades de mercadorias diferentes. Dividindo cada uma das equações do sistema acima pela quantidade total produzida pelo setor correspondente obtemos:

 

 

Observe-se que as razões entre parênteses correspondem à definição dos coeficientes técnicos em termos das quantidades, que indicamos acima. Substituindo:

 

 

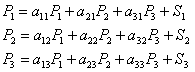
onde S1, S2, S3 correspondem ao valor adicionado por unidade produzida. Supondo que o valor adicionado unitário em cada setor seja proporcional ao seu custo unitário de produção, teríamos:

 

 

Partindo portanto, da desagregação pela ótica dos custos, chegamos a um sistema de preços de produção, representado de forma matricial como

 

 

onde P é o vetor de preços de produção, A| é a transposta da matriz dos coeficientes técnicos e r é a taxa de lucro.

Conhecida a matriz dos coeficientes técnicos, restam como incógnitas os preços e a taxa de lucro. Como uma das mercadorias pode ser escolhida como numerário, restariam três incógnitas: os preços das outras duas e a taxa de lucro. Como temos três equações, o sistema fica determinado.

Sob este ponto de vista, parece que a taxa de lucro do sistema e os preços relativos dependem apenas das condições técnicas de produção. Porém para que este raciocínio faça sentido, é preciso maiores considerações sobre o que estes coeficientes técnicos precisariam estar incluindo.

O leitor mais atento deve ter percebido que até agora não fizemos nenhum comentário sobre os custos com salários. Se tomarmos como base nosso ponto de partida, a contabilidade das matrizes de insumo-produto, na verdade o valor dos salários pagos está incorporado ao valor adicionado.

Por ora faz mais sentido, porém, considerar que por hipótese os coeficientes técnicos estejam incluindo além das quantidades de cada mercadoria utilizadas como insumo, também as quantidades necessárias para proporcionar aos trabalhadores empregados o consumo de certa quantidade das mercadorias produzidas pelos setores considerados. Em outras palavras, vamos supor que os coeficientes técnicos incluem a cesta de subsistência dos trabalhadores.

Neste caso, de fato, uma vez determinada a matriz dos coeficientes técnicos, estariam determinados a taxa de lucro e os preços relativos. Neste caso, porém, a matriz dos coeficientes técnicos não estaria refletindo características estritamente técnicas do sistema econômico considerado. Estaria refletindo adicionalmente características sociais e políticas do sistema econômico considerado, que são fundamentalmente importantes quando mencionamos o conceito de subsistência.

 

Subsistência, excedente e preços de produção

 

O conceito de subsistência é absolutamente essencial no pensamento clássico. A primeira consideração a ser feita sobre esse aspecto diz respeito ao duplo caráter da expressão. O nível de subsistência inclui dois elementos: (a) físico-biológico; (b) histórico-social.

De qualquer modo, pode ser definido como um vetor de quantidades das mercadorias produzidas pelo sistema, que incluam os dois elementos mencionados.

 

 

Voltando ao modelo de quantidades, podemos agora analisá-lo sob outra ótica.

 

	I	II	III	Salários	Excedente	VBP
I	Q11	Q12	Q13	NV1	S1	Q1
II	Q21	Q22	Q23	NV2	S2	Q2
III	Q31	Q32	Q33	NV3	S3	Q3

 

Temos na tabela uma nova coluna de demanda sobre a produção dos três setores: a subsistência, decomposta em termos de N(V1;V2;V3), ou seja as unidades consumidas das três mercadorias pelos N trabalhadores empregados. Somando as quantidades relativas è subsistência com as quantidades das mercadorias utilizadas como insumos (colunas I, II e III), temos o consumo necessário. A diferença entre o produto social (Q1, Q2, Q3) e o consumo necessário é o excedente.

Note que nos termos da tabela a composição do excedente encontra-se definida em termos puramente físicos, ou seja, S1, S2 e S3 são quantidades físicas das três mercadorias produzidas que restam após a dedução do consumo necessário.

Observe-se também que nesta nova versão em quantidades não apresentamos as linhas relativas ao valor adicionado e ao valor bruto da produção. Isto ocorre pela impossibilidade de somar os elementos dispostos nas colunas. Isto porque Q11, Q21 e Q31, por exemplo, representam quantidades de mercadorias diferentes. Para somá-los em termos de valor, é preciso conhecer seus preços.

Pois bem, dada a matriz dos coeficientes técnicos e o salário real, há um conjunto de preços relativos que garante a equalização da taxa de lucro entre os setores. Observe-se que o fato da taxa de lucro ser a mesma em todos os setores nada quer dizer sobre a composição do excedente em termos físicos.

Supondo, por exemplo, que em termos físicos só haja excedente em um dos três setores, isso não significa que os outros setores não terão lucro. Eles terão lucro proporcional aos custos de produção, e esta proporção, em condições de concorrência, tem de ser a mesma para todos os setores, sejam eles produtores de excedente em termos físicos ou não.

A partir dessas considerações, pode-se perceber que os preços de produção associados a uma matriz de coeficientes e um nível de subsistência, e portanto a uma determinada taxa de lucro, são exatamente os preços que garantem a uniformidade desta taxa entre os diferentes setores, embora a proporção em que o excedente é produzido em termos físicos possa ser, e certamente deverá ser, dependente de outros aspectos.

Ao longo do texto as propriedades analíticas associadas a estas considerações ficarão mais claras. A este ponto parece útil mencionar que o modelo de preços de produção só foi exposto de forma completa por Sraffa (1960). Antes de Sraffa, o procedimento teórico para a determinação dos preços relativos sempre esteve associado ao conceito de valor-trabalho.

 

Insumo-produto e valor-trabalho

 

Multiplicando o vetor de coeficientes técnicos de trabalho direto (L) pela matriz de Leontief, obtém-se o vetor de trabalho verticalmente integrado, que representa as unidades de trabalho direta e indiretamente incorporadas a cada unidade das mercadorias consideradas. A razão entre os elementos desse vetor representa, portanto as quantidades relativas de trabalho incorporadas nas mercadorias.

 

voltar
voltar ao roteiro das aulas