CUADRO DE HONOR - 2 -

Las personas cuyos nombres se mencionan a continuación
han respondido correctamente alguno de los acertijos publicados previamente:
Actualizado el 24 de septiembre de 1999

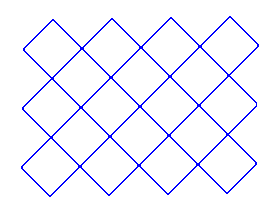
Acertijo (34):
Malla romboidal.
Colocar los números: 1, 6, 8, 9, 11, 12, 15, 16, 18, 19, 21, 22, 25, 26, 30, 31, 36, 37,
40, 41, 42, 45, 46, 47, 48, 49, 50, 51, 56, 57 y 61.
En los nudos de la malla romboidal (ver gráfico) siguiente de modo que, la suma de los cuatro números que estén en los vértices de cualquiera de los dieciocho rombos sea igual a 124.

Ganadores:
Vacío

Respuesta:

Acertijo (35):
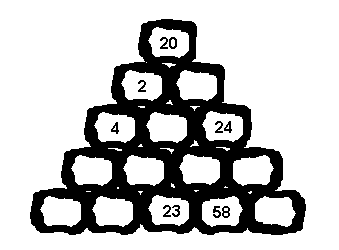El montón de piedras.
Cada una de las piedras del montón (ver gráfico) reposa sobre dos de la fila inferior. El número de cada piedra representa la diferencia entre los números de las piedras sobre las que se sustenta. Completar los números que faltan, sabiendo que en la fila inferior los dígitos del 0 al 9 sólo aparecen una vez en el conjunto de todos los números.

Ganadores:
VACIO

Respuesta:

Acertijo (36):
El posavasos y la servilleta.
Tenemos un posavasos circular y una servilleta cuadrada. Hallar el centro del posavasos con la ayuda únicamente de la servilleta y un lapicero (ver gráfico).

Ganadores:
H. Enrique Garza B.:
1. Tomas la servilleta y la pones sobre el posavasos.
2. Ultilizando uno de los lados de la servilleta mides el diámetro del posavasos (es decir, la distancia más larga que se puede medir de un extremo a otro del círculo) y lo marcas con el lapicero.
3. Ya que tienes marcada la servilleta la doblas a la mitad y marcas dicho punto con el lapicero.
4. Vuelves a colocar la servilleta sobre el posavasos e idicas el centro.... LISTO

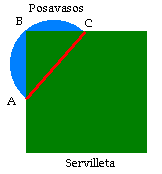
Respuesta:Tomamos la servilleta y colocamos uno de los vértices sobre cualquiera de los puntos de la circunferencia, tal y como se representa en la figura (ver gráfico).
El ángulo definido por ABC es un ángulo recto, luego el segmento AC es un diámetro de la circunferencia. Trazamos con un lapicero la línea AC y repetimos la misma operación eligiendo como B cualquier otro punto del perímetro del posavasos. Una vez trazado el segundo diámetro ya hemos hallado cual es el centro de la circunferencia.

Acertijo (37):
El rey, su hija y su hijo: otro problema de Lewis Carroll.
Un rey, su hija y su hijo estaban encerrados en lo alto de una torre. El monarca pesaba 91 kg, la hija 42 y el hijo 49. Disponían de una polea con una cuerda que llegaba al suelo con un cesto a cada lado, y podían utilizar una cuerda de 35 kg. ¿ Cómo se las arreglaron para bajar, si la diferencia de peso entre los dos cestos no podía ser mayor de siete kilos ?

Ganadores:
Profr. Arbey Grisales (Colombia).
A continuación le expongo una solución al problema de Lewis Carroll.
- En una canasta de la polea se coloca la cuerda y en la otra canasta la niña, por lo tanto la niña baja (pero no se baja de la canasta) y la cuerda queda arriba.
- El rey o el niño tiran la cuerda.
- Se sube en la canasta que está arriba, el niño; y la niña queda arriba.
- En la canasta que quedó abajo se coloca la cuerda, la niña baja y la
cuerda sube
- Se suben el niño y se coloca la cuerda en la canasta que está abajo y en la canasta que está arriba se sube el rey. Por lo tanto el rey baja, el niño y la cuerda quedan arriba.
- Se sube el niño en la canasta que está arriba y la niña en la canasta que está abajo, el niño antes de bajarse tira la cuerda. Por lo tanto la cuerda, el rey y la niña quedan abajo.
- Se sube la niña a la canasta que está abajo. por lo tanto baja el niño y sube la niña
- Se hecha la cuerda en la canasta que está abajo y la niña se sube en la canasta que está arriba. Por lo tanto baja la niña y sube la cuerda.
-Finalmente se baja la niña y por lo tanto la cuerda baja.
De verdad que el problema es un poco complejo y exige para ser solucionado tener en cuenta en forma muy precisa la información suministrada. Al leerlo inicialmente no entendía claramente para qué servía la cuerda y que función cumplía este dato en el problema. Me ayudó mucho el hecho de entender que eran 4 los pesos que estaban en la parte de arriba de la torre (el rey, hijo, hija y cuerda).
Espero que la solución sea correcta. En caso de no ser así, me gustaríasaber en qué parte no se entiende la solución y también si hay un método más sencillo para resolverlo.

Respuesta:
Esta es la secuencia que resuelve el problema:
1.Utilizando la polea, se baja la cuerda hasta el cesto de abajo.
2.Entra la hija en el cesto de arriba, y baja compensada por el peso. La cuerda queda arriba.
3.Baja el hijo y sube la hija.
4.Se baja otra vez la cuerda.
5.Baja el rey y suben el hijo y la cuerda.
6.Baja la cuerda.
7.Baja la hija y sube la cuerda.
8.Baja el hijo y sube la hija.
9.Baja la cuerda.
10.Baja la hija y sube la cuerda.

Acertijo (38):
El abuelo William y el crack de la bolsa.
- Abuelo William, usted es un hombre de edad y, sin embargo, ha conseguido hacer una fortuna en la bolsa. ¿Cómo consiguió sobrevivir al crack de 1929?.
- Vendí todas mis acciones de la mina de oro pocas semanas antes del crack. Una semana vendí la cuarta parte de las acciones, a la semana siguiente otra cuarta parte, la tercera semana otra cuarta parte y la cuarta semana me deshice de todas las acciones que me quedaban por dieciseis dólares. El producto del precio de la venta de la primera semana por el de la última era igual al cuadrado del precio de la segunda semana. El dinero que obtuve por la venta de la segunda semana era igual a la media de la primera y la tercera. El de la última, era mayor que el doble de la primera. Todas las semanas obtuve un número par de dólares.
¿Cuáles fueron los precios de las tres primeras semanas?

Ganadores:
Vacío

Respuesta:
Llamaremos p1, p2, p3 y p4 a los precios respectivos y sabemos que p4 = 16.
En el enunciado se dice que p4 > 2p1. Por otra parte, sabemos que p1.p4 es igual al cuadrado de p2. p1 sólo puede valer 2, 4 ó 6, porque debe ser par y si vale 8 o más no se cumple la condición p4 > 2.p1 . Entonces p1.p4 puede tomar los valores 32, 64 ó 96. De estos tres valores sólo 64 es un cuadrado, así que p2 = 8 y p1 = 4. Como p2 es la media de p1 y p3, entonces p3 = 12.

Acertijo (39):
Los calcetines de papá hormiga.
Papá hormiga va a salir de casa para buscar miel. Como todas las hormigas, tiene un problema para encontrar sus calcetines. A papá hormiga no le preocupan estas trivialidades, estará contento si consigue calzarse cuatro calcetines iguales (por si aún no lo sabías, las hormigas tienen seis patas). Si tiene 7 juegos diferentes de calcetines, ¿de cuántas maneras distintas puede lograr llevar cuatro calcetines iguales?

Ganadores:
VACIO

Respuesta:
Tenemos 7 juegos de calcetines de distinto color (por ejemplo 6 rojos, 6 azules, 6 negros... etc..), Para que al menos 4 de 6 sean iguales, tenemos que considerar primero las probabilidades de tener los 6 calcetines del mismo color, en segundo lugar, 5 iguales y uno diferente, en tercer lugar , 4 iguales con otros dos del mismo color (por ejemplo, 4 rojos y dos azules) y, por último 4 iguales y otros dos de diferentes colores (por ejemplo, 4 rojos, 1 azul y 1 rosa). Hay siete posibilidades de que todos los calcetines sean iguales pues hay siete juegos de colores. Hay 7 formas de tener 5 calcetines del mismo color y 6 posibles colores para el calcetín restante. Como el calcetín que no casa puede colocarse en cualquiera de las seis patas, en este caso, hay seis formas posibles de ponerse los calcetines. Por tanto, para este segundo supuesto hay 7 x 6 x 6 = 252 formas de ponerse los calcetines. En el tercer caso, hay 7 posibilidades de elegir 4 calcetines del mismo color , y 6 posibilidades para los dos calcetines restantes, que son del mismo color. Suponiendo que los 6 calcetines fuesen diferentes , habría 6! formas de ponerse los calcetines,pero tenemos que dividir por 4! and 2! puesto que los cuatro calcetines iguales y los dos restantes son indistinguibles por color.. Obtenemos para el tercer supesto (7 x 6 x 6!)/(4! x 2!) = 630 formas. En el último caso hay 7 formas de escoger los cuatro calcetines iguales, 6 posibilidades para elegir el primer calcetín de otro color y 5, para el segundo. En este caso sólo tenemos que dividir por 4!, puesto que los dos calcetines restantes son de distinto color.
Por tanto, en el cuarto caso hay 7 x 6 x 5 x (6!/4!) = 6300 formas. Sumando los cuatro supuestos, papá hormiga tiene 7 + 252 + 630 + 6300 = 7189 posibles formas de ponerse los calcetines.

Acertijo (40):
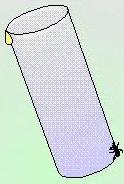Papá hormiga y el cilindro (ver gráfico).

Papá hormiga quiere trepar a lo alto del cilindro para alcanzar la gota de miel que está en la parte superior y diametralmente opuesta al lugar en el que él se encuentra en la base. El cilindro tiene 5 cm de radio y 20 de altura. Para complicar las cosas, la gota de miel está bajando a una velocidad de 1,5 cm por segunda. Si papá hormiga trepa a 2,5 cm por segundo ¿a qué altura se encontrará con la miel, y cuánto tardará en hacerlo?

Ganadores:
VACIO

Respuesta:
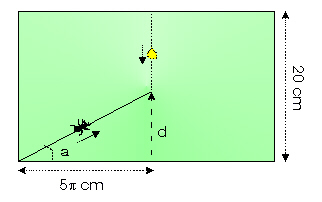Si desarrollamos la superficie del cilindro obtenemos un rectángulo de 20 cm por 10 x 3.14 cm. La figura representa la situación .
Para resolver este problema hemos de despejar dos incógnitas el ángulo a, que describe la trayectoria de la hormiga y el tiempo t necesario para llegar a la miel.
La componente vertical d de la distancia recorrida por la hormiga en el tiempo t, más la distancia que baja la gota de miel suman los 20 cm de altura del cilindro.
(2.5 sina x t)+ 1.5t = 20
Segundo. El componente horizontal de la distancia recorrida por la hormiga es igual a la mitad de la longitud del rectángulo
2.5 cosa x t = 5 x 3.14
Resoviendo, se obtine que a = 30.1 grados y t = 7.26 sec.

Acertijo (41):

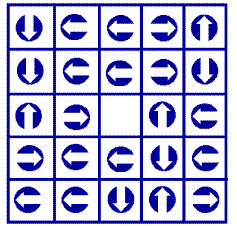
Secuencia de flechas.
¿Hacia dónde debería apuntar la flecha que falta en el centro del dibujo? (ver gráfico)

Ganadores:

Respuesta:
La flecha debe apuntar hacia arriba. la secuencia es abajo, izquierda, izquierda, derecha, arriba, en una espiral en el sentido del reloj desde la parte superior izquierda.

Acertijo (42):
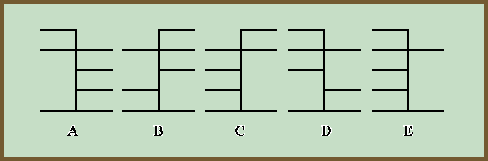Figuras orientales.
¿Cuál de las siguientes figuras sobra en la serie? (ver gráfico)

Ganadores:
Constanza Spada D. (Guadalajara):
La E?

Respuesta:
A es la imagen especular de C, mientras que B es la imagen especular de D. Por tanto, la figura que sobra en esta serie es la E.

Volver al Menu del Pequeño Edison