Chapter Four

Results of the Remember - an -Instance Multiple-Choice Sub-test (RIM )

Table (1). A Three-Way ANOVA summary table for question types, levels, and student’s ability on RIM sub-test.

Source of models	DF	SS	MS	F-test	P value
Question type (A)	1	0.055	0.005	0.184	0.6687
Question level (B)	2	5.391	2.695	9.079	0.0002 **
AB	2	0.143	0.072	0.242	0.7858
Student’s ability(C)	2	3.656	1.828	6.158	0.0030 **
AC	2	0.004	0.002	0.007	0.9926
BC	4	1.644	0.411	1.385	0.2445
ABC	4	0.997	0.249	0.85	0.5031
Error	102	30.28	.297

The post hoc ANOVA by using a Scheffe test showed at .05 level of significance that the mean of the experimental group who received questions on Remember a Generality (RG) level (x= 2.95 ) was higher than the mean of those who received either Remember an Instance (RI) questions (x =2.62), or Use a Generality ones (x =2.47). The last two means did not differ significantly (See, Table 2).
Table ( 2 ). Means, standard deviations and number of students in each cell for question types and question levels on a RIM sub-test.

* P > .05 
** P > .01
In terms of student’s ability levels, Scheffe test showed that the mean of high ability students was higher significantly than the mean of low ability students ( x = 2.82 versus x=2.28 ), and the mean of medium ability was higher than the mean of low ones ( x = 2.68 versus 2.28 ). Whereas, Scheffe test did not reveal a significant difference between the mean of medium ability and the high one ( x = 2.68 versus 2.82 ) ( See, Table 3 ). 

Table (3). Means, standard deviations, and number of students for question types, and student’s ability on a RIM sub-test.

Results of the Remember - a - Generality Multiple-Choice Sub -test (RGM) 

On the Remember - a - Generality Multiple-Choice Sub-test (RGM), general ‘F’ revealed significant differences for question type (P< .0445) and student’s ability (P<.0008);‘F’ test also revealed a significant interaction between question types and question levels (P< .0025) which indicated that groups who received remember instance essay questions performed higher than those who received remember instance multiple-choice questions, whereas the performance did not differ for those who received either multiple-choice or essay questions measuring RG or UG levels (See, Table 4 & 5 ).
Table (4). A Three-Way ANOVA summary table for question types, levels, and student’s ability on a RGM sub-test.
 

Source	DF	SS	MS	F-test	P value
Question type (A)	1	2.37	2.37	4.14	0.0445 *
Question level (B)	2	2.03	1.01	1.77	0.1753
AB	2	7.30	3.65	6.36	0.0025 **
Student’s ability(C)	2	8.77	4.38	7.64	0.0008 **
AC	2	2.24	1.12	1.95	0.1468
BC	4	4.22	1.05	1.84	0.1266
ABC	4	1.12	0.28	0.49	0.742
Error	102	58.48	.573

The post hoc ANOVA (by using a Scheffe test at (.05) level of significance) did not show significant differences for question type: essay (x= 2.23 ) and multiple-choice one (x = 2.43 ), though the essay type mean was higher than the multiple-choice one ( see, Table 5 ).

Table (5). Means, standard deviations, and number of students in each cell for question types, and levels on a RGM sub-test.

On the other hand, Scheffe test showed significant differences at (.05) for student’s ability which indicated that the high student’s ability mean was higher than the low student’s ability one (x = 2.55 versus 1.85 ), whereas, Scheffe test didn’t reveal any significant difference neither between low and medium student’s ability means ( x = 1.85 versus 2.26 ) nor between high and mid student’s ability means ( x = 2.55 versus 2.26 ). See, Table ( 6 ).

Table(6). Means and the number of students in each cell for question types, and students’ ability on a RGM sub-test.

Results of the Use - a - Generality Multiple-Choice Sub-Test ( UGM )

Table(7). A Three-Way ANOVA summary table for question types, levels, and student’s ability on a UGM sub-test.

Source	DF	SS	MS	F-test	P-value
Question type (A)	1	0.559	0.559	0.845	0.360
Question level (B)	2	0.874	0.437	0.660	0.519
AB	2	0.139	0.069	0.105	0.900
Student’s ability(C)	2	10.34	5.170	7.810	0.0007 *
AC	2	0.867	0.434	0.655	0.521
BC	4	1.450	0.362	0.547	0.701
ABC	4	5.235	1.309	1.977	0.103
Error	102	67.52	.66

The post hoc ANOVA by using Scheffe test showed at .05 level of significance that the mean of high ability students was higher than the low one ( x = 2.37 versus 1.57 ), whereas, there were no significant differences neither between low and medium student’s ability means ( x = 1.57 versus 2.07 ) nor between high and medium student’s ability means (x = 2.37 versus 2.07 ) ( See, Table 8 ).

Table (8). Means and number of students in each cell for question types, and student’s ability on a UGM sub-test.

Results of the Remember - an - Instance Essay Sub-Test ( RIE ) 

On the remember - an - instance essay sub-test ( RIE ), general ‘F’ revealed significant differences for question types (P< .0006), question levels (P< .0256 ), and student’s ability ( P < .0323). ‘F’ test also revealed a significant interaction between question types and question levels (P< .0047), which indicated that remember - a - generality multiple-choice (RGM) group performed better (x = 2.6) than remember - a - generality essay RGE (x= 1.2), and remember - an - instance multiple-choice (RIM) (x = 2.4) performed better than remember - an - instance essay (RIE) (x =1.3), whereas the performance of use - a - generality groups didn’t differ from the multiple-choice type questions to essay ones ( See, Table 9).

Table(9). A Three-Way ANOVA summary table for question types, levels, and student’s ability on a RIE sub-test .

Source	DF	SS	MS	F-test	P-value
Question type (A)	1	14.081	14.081	12.428	0.0006 **
Question level (B)	2	8.614	4.307	3.802	0.0256 *
AB	2	7.138	3.569	3.150	0.0470 *
Student’s ability(C)	2	8.045	4.023	3.551	0.0323 *
AC	2	1.504	0.752	0.664	0.5171
BC	4	2.770	0.962	0.611	0.6555
ABC	4	2.395	0.599	0.528	0.7151
Error	102	115.56	1.133

In terms of question types, Scheffe test showed at (.05) level of significance that groups who got multiple-choice type questions had higher mean than groups who got essay type questions (x = 2.06 vs.1.21). In terms of question levels, Scheffe test revealed that groups who got remember - a - generality level questions had a higher means (x= 2.6 ) than those who got remember - an - instance (x = 2.4) or use - a - generality (x = 1.1) levels questions. In terms of ability levels, the high ability students’ mean was higher than the low ability students’ one ( x = 1.86 versus 1.09 ) (See, Table 10 ).

Table (10). Means, standard deviations, and number of students in each cell for question types, and levels on a RIE sub-test.

At the same time Scheffe test did not reveal any significant difference between medium and low student’s ability ( x=1.61 versus x=1.09) nor between medium and high ability students ( x = 1.61 versus 1.86 ) ( See, Table 11) .

Table ( 11). Means, standard deviations and number of students in each cell for question types, and student’s ability on a RIE sub-test.

Results of the Remember - a - Generality Essay Sub-Test ( RGE )

Table (12). A Three-Way ANOVA summary table for question types, levels, and student’s ability on a RGE sub-test.

Source	DF	SS	MS	F-test	P-value
Question type (A)	1	4.06	14.06	1.78	0.184
Question level (B)	2	13.04	6.52	2.86	0.061
AB	2	5.78	2.89	1.27	0.285
Student’s ability(C)	2	44.59	22.29	9.78	0.001 **
AC	2	2.48	1.24	0.54	0.581
BC	4	2.81	0.70	0.30	0.871
ABC	4	4.09	1.02	0.45	0.772
Error	102	232.41	2.27

The Post Hoc ANOVA by using a Scheffe test at (.05) level of significance revealed that high ability students performed better than low ability ones (x =3.69 versus 2), whereas the medium ability students performed better than the low ability ones ( x = 3.12 versus 2 ). At the same time, Scheffe test did not reveal any significant difference between the mean of high ability students and the mean of the medium one ( x = 3.69 versus 3.12) (See, Table 13 ).

Table (13). Means, standard deviations and number of students in each cell for question types, and student’s ability on a RGE sub-test.

Results of the Use - a - Generality Essay Sub-Test ( UGE ) 

Table (14). A Three-Way ANOVA summary table for question types, levels, and student’s ability on a UGE sub-test.

Source	DF	SS	MS	F-test	P-value
Question type (A)	1	0.67	0.67	0.98	0.3235
Question level (B)	2	4.76	2.38	3.49	0.0339 *
AB	2	1.24	0.62	0.91	0.405
Student’s ability(C)	2	3.32	1.66	2.44	0.0922
AC	2	0.63	0.41	0.61	0.5428
BC	4	2.62	0.65	0.96	0.4304
ABC	4	2.14	0.53	0.78	0.5359
Error	102	69.42	.68

But the post hoc ANOVA by using Scheffe test at (.05)level of significance did not reveal any significant difference between the means of three question levels ( RI, RG, and UG) ( x = 1.05 vs. 1.45 vs. 1.35 ), though the mean of RG group was higher than the UG or RI ones (See, Table 15).

Table ( 15 ). Means, standard deviations, and number of students in each cell for question types, and levels on a UGE sub-test.

Results of the Total Multiple-Choice Test

Table (16). A Three-Way ANOVA summary table for the total multiple- choice test.

Source	DF	SS	MS	F-test	P-value
Question type (A)	1	4.222	4.222	1.985	0.162
Question level (B)	2	9.611	4.806	2.259	0.109
AB	2	7.222	3.611	1.697	0.188
Student’s ability(C)	2	65.20	32.60	15.32	0.0001 **
AC	2	3.574	1.767	0.840	0.4347
BC	4	8.005	2.001	0.941	0.4436
ABC	4	1.676	0.419	0.197	0.9394
Error	102	216.99	2.12

The post hoc ANOVA by using Scheffe test at (.05) level of significance revealed significant difference between high student’s ability versus the low ones (x = 7.759 versus x=5.714), and medium student’s ability versus low ones (x = 7.024 versus x =5.714 ). But it failed to reveal a significant difference between the mean of high versus medium ability students ( x = 7.759 versus x = 7.024 ) (See, Table 17 ).

Table (17). Means, standard deviations and number of students in each cell for the total multiple-choice test.

Results of the Total Essay Test

Table (18). A Three-Way ANOVA summary table for the total essay test.

Source	DF	SS	MS	F-test	P-value
Question type (A)	1	0.842	0.84	0.12	0.7216
Question level (B)	2	16.29	8.14	1.23	0.2951
AB	2	13.10	6.55	0.99	0.3739
Student’s ability(C)	2	113.2	56.6	8.58	0.0004 **
AC	2	1.593	0.79	0.12	0.8864
BC	4	9.883	2.47	0.37	0.8264
ABC	4	11.44	2.86	0.43	0.784
Error	102	672.9	6.59

The post hoc ANOVA by using Scheffe test revealed significant difference between the levels of student’s ability i.e., high versus low (x = 7.017 versus x= 4.286) only. But it did not reveal any significant difference between high versus medium ability students ( x = 7.017 vs. x = 5.817 ) nor between medium versus low ( x = 5.817 versus x = 4.286 ) ( See, Table 19).

Table (19). Means standard deviations and number of students in each cell for the total essay test.

The Results of the Overall Test

On the overall test, there were the following results:

Table (20). A Three-Way ANOVA summary table for the overall learning test. 

Source	DF	SS	MS	F-test	P-value
Question type (A)	1	1.292	1.292	0.093	0.7606
Question level (B)	2	48.21	224.17	1.740	0.1806
AB	2	20.41	10.20	0.737	0.4811
Student’s ability(C)	2	349.6	174.8	12.62	0.0001 **
AC	2	9.441	4.721	0.341	0.712
BC	4	17.81	4.453	0.321	0.863
ABC	4	16.12	4.031	0.291	0.8832
Error	102	1412.7	13.85

Table (20:1) shows the mean of each test type. 
 

Test Types	Essay	Multiple-choice	Total
Mean	13.33	12.22	13.27

Figure (1) shows the mean scores of essay and multiple-choice questions on the overall learning test.

2. General ‘F’ didn’t also show significant differences among the three levels of questions (RI, RG, and UG) (p = .180), thus, there was no need to use a Scheffe test. By this result, we answered the second question of this study
"Which level of questions (RI, RG, and UG ) has more effect on students’ overall learning?", by stating that there were no differences among three of them, though the mean of RG group was higher than RI and UG groups (See,Table 22:2 and Figure 2). At the same time, we accepted the second null hypothesis which says "There are no significant differences at ( 0.05 ) a priori level of significance among the three levels of questions (RI, RG, UG ) on all levels of learning. 

Table (20:2) shows the mean scores of each level of questions.

Test levels	RI	RG	UG	Total
Mean	12.63	14.30	12.90	13.27

Figure (2) shows the mean differences between the three levels of questions (RI, RG, and UG) on the overall learning test.

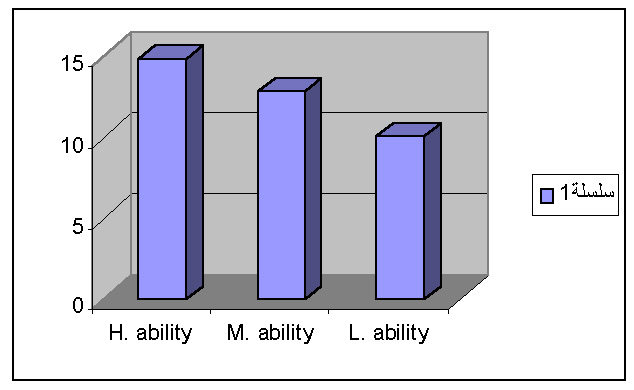
3. General ‘F’ showed significant differences among the three levels of student’s ability (high, medium, and low) (p >.0001). The post hoc ANOVA (by using Scheffe test) revealed that there is a significant difference between high and low student’s ability (x = 14.776 versus 10) and between medium and low student’s ability ( x = 12.841 versus 10 ). But it did not reveal any significant difference between high versus medium of student’s ability means (x =14.776 vs. x = 12.841 ). By this result, we answered the third question of this study "Which level of student’s ability (high, medium, or low) has more effect on the students’ overall learning?, by stating that the performance of the high ability students was better than the performance of the medium and low ability ones on the overall learning (See, Table 20:3 and Figure 3 ). At the same time , we rejected the third null hypothesis of this study which says "There are no significant differences at ( 0.05 ) a priori level of significance among the effects of the three levels of the student’s ability ( high, medium, and low ) on all levels of learning. 

Table (20:3) shows the mean scores of each level of student’s ability.
 

Student’s ability level	high	medium	low	Total
Mean	14.77	12.84	10.00	13.27

Figure (3) shows the performance of the three levels of student’s ability (high, medium, and low) on the overall learning test.

4. In terms of the interaction between types, levels and student’s ability, general ‘F’ didn’t show any significant interaction between question types (essay versus multiple-choice) and question levels (RI, RG, and UG) (p = .4811), nor between question levels (RI, RG, and UG) and student’s ability (high, medium, and low) (p =.863), or between question types (essay versus multiple-choice ) and student’s ability (high, medium, and low) (p = .712 ). General ‘F’ didn’t also show a significant interaction among question types (essay versus multiple-choice), question levels (RI, RG, and UG) and student’s ability (high, medium, and low) (p = .8832 ) simultaneously. By these results, we answered the fourth, fifth, sixth, and seventh questions of this study, they are question 4: "Is there an interaction between question types ( essay versus objective) and question levels (RI, RG, UG) on students’ overall learning ?", question 5 "Is there an interaction between question levels ( RI, RG, UG ) and student’s ability ( high, medium, low ) on students’ overall learning ?", question 6 "Is there an interaction between question types ( essay versus objective ) and student’s ability on students’ overall learning ?", question 7: Is there an interaction between types and levels of questions and student’s ability on students’ overall learning ?. 
At the same time, we accepted the fourth, fifth, sixth, and seventh hypotheses, they are: 
Hypothesis 4: There is no significant interaction at ( 0.05 ) a priori level of significance between question types and their levels on all levels of learning, 
hypothesis 5 "There is no significant interaction at ( 0.05 ) a priori level of significance between question types and student’s ability on all levels of learning", hypothesis 6 "There is no significant interaction at (0.05 ) a priori level of significance between question levels and student’s ability on all levels of learning", hypothesis 7 "There is no significant interaction at (0.05) a priori level of significance between question types, levels, and students’ ability on all levels of learning", by stating that there were no interactions among question types, levels and student’s ability (See, Table 20:4).

Table (20:4) shows the interaction among types, levels of questions and student’s ability.

Q. levels

RI

RG

UG

Total

S. ability	H	M	L	H	M	L	H	M	L	Total
Essay x n	15 10	12.1 6	9.7 4	14.3 9	14.1 8	10.3 3	14.2 10	13.7 6	10 4	13.3 60
Multiple x n	14.2 9	11.6 8	7.5 3	16.5 11	13.5 6	11.6 3	13.8 9	12 7	10.6 4	13.2 60
Total x n	14.6 19	11.8 14	8.7 7	15.6 20	13.8 14	11 6	14 19	12.8 13	10.3 8	13.27 120

Top
Results of the Experimental and Control Groups

Table (21). Means, standard deviations, and number of students in each cell of the experimental and control groups on the overall multiple-choice test.

Group	RIM	RGM	UGM	RIE	RGE	UGE	Control
x (SD) n	6.45 (1.95) 20	7.5 (1.1) 20	6.95 (1.66) 20	7.45 (1.43) 20	7.7 (1.59) 20	6.85 (1.75) 20	6.15 (1.34) 20

General ‘F’, on the other hand, didn’t show any significant differences between the experimental and control groups on the total essay test (p > .2211) (See, Table 22), nor on the overall test (p > .1685). 

Table (22). Means, standard deviations, and number of students in each cell of the experimental and control groups on the overall essay test.

Group	RIM	RGM	UGM	RIE	RGE	UGE	Control
x (SD) n	5.72 3.68 20	7.45 2.41 20	5.6 2.38 20	5.65 2.27 20	5.95 2.73 20	6.4 2.20 20	5.3 3.08 20

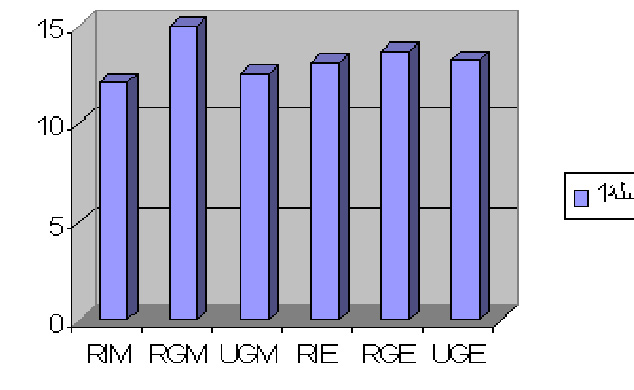
Thus, there was no need to use Scheffe test for post hoc ANOVA. By these results, we answered the last question of this study which says"Are there significant differences between the performance of the experimental groups which manipulated questions during the experiment compared with the performance of the control group which did not manipulate any questions during the experiment?", by stating that there were no differences among the means of all groups, though the mean scores of (RG) group, then the mean scores of (UG) was highest, whereas the mean scores of the control group was the lowest (See, Table 23 and Figure 4 ). At the same time, we accepted the eighth null hypothesis which says "There is no significant difference between the control groups’ performance compared with the experimental groups’ performance".

Table (23). Means, standard deviations, and number of students in each cell of the experimental and control groups on the overall learning.

Group	RIM	RGM	UGM	RIE	RGE	UGE	Control
x (SD) n	12.17 5.33 20	14.95 3.33 20	12.55 3.60 20	13.1 3.46 20	13.65 4.04 20	13.25 3.74 20	11.5 4.16 20

Top
Figure (4) shows the six experimental groups and the control group on the overall learning test.