Select a colour scheme:

The Proof

Now that we know what we need to prove, we can start the proof. The proof will use some discrete mathematics. I present the proof as simple as possible (as I'm not that good in discrete mathematics myself), with explanations throughout the proof.

First, we write down what we know, our starting point.

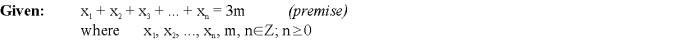
This means that if we have the integer 123, our premise says that 1+2+3 is divisible by 3.

Next, we write what we want to prove, our destination point.

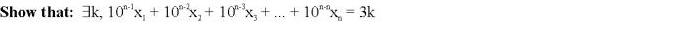
This means that if we have the integer 123, we want to show that 123 is divisible by 3.

Now, we need to somehow "connect" these two points. How do we connect them? By showing the logical steps starting from the starting point until we hit the destination point. There are a number of ways to do this. Here, we use proving by contradiction. How does proving by contradiction work? We make an assumption. Starting from this assumption, we make a series of reasoning. If we meet a contradiction on our way, then our assumption must be wrong.

Here is an example of proving by contradiction. We see a cup of coffee on the table. As there is no steam coming out, we assume that the coffee is cold. Touching the cup, we feel heat on our hand. From physics, we know that cold coffee cannot give out heat. Thus, our assumption is wrong. The coffee is not cold. (At least, it is not colder than our body temperature.)

Back to our original proof, we assume the opposite (the logical inverse) of what we want to prove. If we somehow meet a contradiction, then what we want to prove must be correct. So, here is our assumption*.

From the assumption, we can make the following steps using simple algebra.
At this point, we are actually close to our destination. If we can factorize 3 from the right hand side, we show that the right hand side is NOT divisible by 3. We need a side proof to help our main proof.
Note that we want to prove for all possible values of n (which is infinitely many). It is impossible for us to show all cases one by one. We must use induction principle.
Now, we can continue the main proof and factorize 3 on the right hand side.
Here, we hit a contradiction.
Why is this a contradiction? Well, if we have the integer 123, the premise says that 1+2+3 is divisible by 3. However, the result obtained from our reasoning says that 1+2+3 equals to 3j+h, where j and h are some integers, and h is not divisible by 3 (this is stated in the assumption). In other words, the result says that 1+2+3 is not divisible by 3.
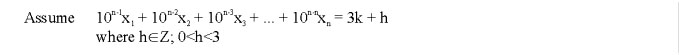
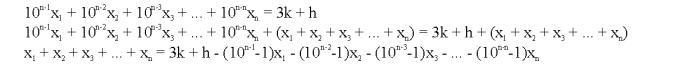
Since a number cannot be both divisible and not divisible by 3 at the same time, we hit a contradiction. Thus, the logical inverse of our assumption is correct.

In conclusion, we have proven that the trick really does work for all integers.

Footnote:
If you are interested in the complete proof without explanation, you can see it here.

Acknowledgement:
*Thanks to Leif Schjeide (lschjeide@yahoo.com) for pointing out that the value of the remainder h in the assumption is incorrect.

Any follow-ups, comments or objections to this proof?
Feel free contact me dennyisk@comp.nus.edu.sg.

Last edited: Wednesday, 23 October 2002
The material published on this Web page is personal, and is not endorsed by or the responsibility of the National University of Singapore.
1