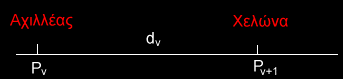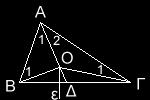
Υπάρχουν,όσο και αν φαίνεται παράξενο,μαθηματικά συμπεράσματα που βρίσκονται σε πλήρη αντίθεση με την κοινή λογική,τη διαίσθηση ή την φαντασία μας.Τέτοιοι ισχυρισμοί λέγονται « παράδοξα ».

Τα μαθηματικά παράδοξα διακρίνονται σε τρεις κυρίως κατηγορίες.

1. Τα αντιφατικά και άτοπα συμπεράσματα που οφείλονται σε κρυμμένα αποδεικτικά λάθη
2. Τα θεωρήματα που φαίνονται παράξενα ή και απίστευτα
3. Τα λογικά παράδοξα,τα οποία αναφέρονται στη θεωρία των συνόλων και των λογικών τύπων

Η τρίτη κατηγορία είναι η σπουδαιότερη και μάλιστα οδήγησε σε επανεξέταση των θεμελίων των Μαθηματικών στις αρχές του αιώνα από τον μαθηκατικό και φιλόσοφο B. Russel.Μερικά χαρακτηριστικά παραδείγματα ακολουθούν.

• Κάθε τρίγωνο είναι ισοσκελές

Έστω τρίγωνο ΑΒΓ,η διχοτόμος ΑΔ της γωνίας του Α,η μεσοκάθετη ε της πλευράς του ΒΓ και το σημείο τομής Ο των ΑΔ και ε.Τα τρίωνα ΑΟΒ,ΑΟΓ (αφού το Ο είναι σημείο της ε) και Α1=Α2.Έτσι αφού Β1=Γ1#180° ,είναι Β1=Γ1 και επομένως τα τρίγωνα ΑΟΒ και ΑΟΓ θα είναι ίσα.Δηλαδή ΑΟΒ=ΑΟΓ. Άρα ΑΒ=ΑΓ

Το συμπέρασμα οφείλεται σε αποδεικτικό λάθος,μια και το Ο δεν είναι εσωτερικό σημείο του τριγώνου ΑΒΓ όπως κακώς είναι στο σχήμα.

• Τα μήκη όλων των κύκλων είναι ίσα

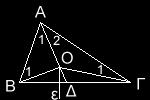
Θεωρούμε δύο ομόκεντρους κύκλους κέντρου Κ και ακτίνας Ρ,κέντρου Κ και ακτίνας ρ αντίστοιχα με Ρ>ρ.Ο κύκλος (Κ,Ρ) κυλιέται πάνω σε μια ευθεία έτσι ώστε η ακτίνα του ΚΑ να εκτελέσει μια πλήρη περιστροφή.Τότε το μήκος του τμήματος ΑΑ' είναι ίσο με το μήκος του κύκλου (Κ,ρ).Κατά την περιστροφή όμως της ΚΑ περιστρέφεται και η ΚΒ, οπότε το μήκος του ΒΒ' είναι ίσο με το μήκος του κύκλου (Κ,ρ).Από από ορθογώνιο όμως ΑΒΒ'Α έχουμε ΑΑ'=ΒΒ'.

Το προηγούμενο παράδοξο οφείλεται στο γεγονός ότι εκτός από την περιστροφική κίνηση εκτελείται και μια περιστροφική κίνηση για τον κύκλο (Κ,ρ) η οποία δεν γίνεται αντιληπτή.

• Ο Αχιλλέας και η χελώνα

Ο Ζήνων ο Ελεάτης τον 5 αιώνα π.Χ προκάλεσε σύγχυση στους σοφούς της εποχής τουμε τον εξής ισχυρισμό: Ο γοργοπόδαρος Αχιλλέας,παρά τη μεγάλη του προσπάθεια,δεν μπορεί ποτέ να φτάσει μια χελώνα που τρέχει 100 πιο αργά από αυτόν σε ένα αγώνα δρόμου.Για λόγους δικαιοσύνης ο Ζήνων έδωσε στην χελώνα προβάδισμα 1 στάδιο (~150 μ).Τον ισχυρισμό του αυτό ο Ζήνων τον δικαιολογούσε ως εξής: Όταν ο Αχιλλέας φτάσει στην αρχική θέση, έστω Ρ1 αυτή,της χελώνας τότε η χελώνα θα βρίσκεται ήδη λίγο μακρύτερα έστω στη θέση Ρ2.Όταν ο Αχιλλέας φτάσει στη Ρ2 η χελώνα θα βρίσκεται λίγο μακρύτερα στη θέση Ρ3 κ.ο.κΔηλαδή η χελώνα θα έχει πάντα ένα προβάδισμα dν. Όταν ο Αχιλλέας θα διανύσει το διάστημα dν, η χελώνα,αφού τρέχει 100 φορές πιο αργά,θα διανύσει διάστημα dν+1=1/100*dν.Δημιουργείτε έτσι μια ακολουθία διαστημάτων dν στα οποία προηγείται η χελώνα.Η ακολουθία αυτή είναι φθίνουσα γεωμετρική πρόοδος με πρώτο όρο do=1 και λόγο λ=1/100.Δηλαδή η απόσταση του Αχιλλέα από την Χελώνα συνεχώς μικραίνει.Το διάστημα που πρέπει να διανύσει ο Αχιλλέας για να φτάσει την χελώνα είναι S=do/1-λ. Ή S=100/99.Δηλαδή μόλις ο Αχιλλέας διανύσει απόσταση 100/99 σταδίων η απόσταση του από την χελώνα θα είναι μηδενική,δηλαδή θα έχει φθάσει τη χελώνα,