taijiquan

Tai Chi postures and catenary curve (*)

It seems that catenary curve is what is meant by Gua (Kwa) (as described in (1) and in a way could be the Western analogue or counterpart for the notion of Gua (Kwa). 

1 Catenary curve

The main thing about catenary curve (the shape a free-hanging chain takes, when fixed at two ends) is (see e.g. 2):

- When hanging, the chain links experience only tesion along the chain and no compression whatsoever;

- When flipped upside down, the catenary-shaped construction (an inverted catenary arch, as well as catenoid vault and dome, actively employed in architecture (see e.g. 3)) experiences pure compression forces along the arch and no tension at all in any direction

"The catenary is the ideal form for an arch which supports only itself. If made of individual elements whose contacting surfaces are perpendicular to the curve of the arch, no significant shear forces will be present at the joints, and the thrust into the ground will be directly along the line of the arch." (2)

Thus, the catenary is the theoretically most optimal and economical shape for standing or hanging constructions. It is described by a clear and simple mathematical formula.

2 Gua (Kwa) and catenary

It seems that much of the statics of Tai Chi postures may be based on catenaries:

The "relaxation" shapes of trunk and limbs (e.g. the shape of arm in Single Whip) form "hanging" catenaries and therefore experience only tension forces along
the limbs.

The supporting shapes form inverted catenaries (in the legs, soles, spine etc), which experience no stretching, but only compression, which is passed purely along the bones with (almost) no muscles involved.

The above citation applied to engineering constructions, but in fact can be read as an anathomical statement:

"[N]o significant shear forces will be present at the joints." (2)

This means, that if we look at our limbs and body parts as at chains made of joint-connected bones, the closest approximation of catenary curve is the optimal shape for those "chains", because then all the forces (produced in our body by gravity or be contact with an obstacle: a wall or opponent's body) will act along our catenary-aligned bones.

If it is true, then in supporting shapes (e.g. the position of our legs in Tai Chi postures), the minimal involvement of muscles will be achieved. Indeed, the inverted catenary does not experience tension forces whatsoever, whereas the way the muscles work is contraction, i.e. purely opposing the tension forces is the only thing our muscles are able to do by their nature. In the absense (or minimizing) the tension forces (achieved by approximation of inverted catenary) the muscle contraction also will be naturally minimized.

Therefore, Tai Chi postures could be approximated by a system of inverted and "hanging" catenary curves in projections on any plane, minimizing our muscle contraction and thus, maximazing our relaxation.

Hopefully, this could give more explanatory power to our Tai Chi discourse:

For example, it resolves the seeming contradiction between "pressure" and "suspension" in the Tai Chi texts, as they both refer to catenaries: "pressure" to inverted catenary and "suspension" to the "hanging" one, as well as gives us a hint how to improve our postures.

Say, we could try to think about "Gua (Kwa) of armpit" or "Gua (Kwa) of palm" (1) as a a dome-shaped surface swept by rotation of a catenary curve, which again will be the most economical shape providing maximum strength and should give a greater mobility and relaxed firmness to our joints.

The property of the inverted catenary that

"the thrust into the ground will be directly along the line of the arch" (2)

sounds strikingly similar to (and probably represents the mechanical formalization of) William C. C. Chen's description of Tai Chi root based on "three nails":

"When the foot is rooted, these three points grip like three nails penetrating the ground." (4)

as in terms of the physics of catenary, all the force is channeled through the arch of the leg into the arch of the sole and then into the ground via the "three nails", where the "nail" of the heal represents one end of the arch and the "nails" of the big toe and of the ball of the foot represent the other end of it.

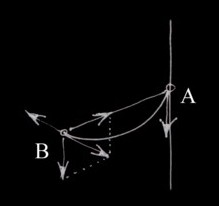
3 Hanging or inverted?

It may seem that catenary geometry is not applicable to contstructions that look to be fixed only at one end, for example, the arm stretched forward or our backbone, when we bend down.

However, in this case our bones are fixed at both ends: one end is attached, say, to our trunk (maybe through other joints ), while the other is held in the air by a muscle (relaxed or contracted).

Figure 3.1 informally illustrates that in this case we still are dealing with an inverted catenary:

Fig. 3.1

 Let us suppose that the curve AB is "made of individual heavy elements whose contacting surfaces are perpendicular to the curve", something like our backbone. A and B also are connected by a string. The curve AB is firmly attached, say, to a wall at point A. The point B is hanging.When left free, this system will stabilize in the position like on the Figure 1. The curve AB will take a catenary shape according to the laws of the inverted catenary for the following reason:

Three forces are applied to the point B: the force of gravity, the tension of the string AB and the force coming from the compression of the joints. As the system has stabilized, the sum of those three forces should be zero. Therefore, the force from the joint (opposed to the sum of the gravity and tension forces) should be tangent to the curve AB. As point A is fixed, the force should be tangent on that side as well. But this is exactly how the forces are applied to the construction with joints to make it shaping an inverted catenary.(**)

Thus, the most relaxed position for the limbs or bone structures  fixed "only on one side" still seems to be a catenary (an inverted catenary).

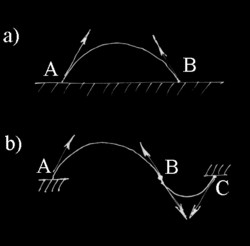
4 Connected catenaries and being connected in Tai Chi

Not every chain of bones, tendons, and other tissues can assume a shape approximating catenary. However, several connected catenaries (in reality, catenary approximations) can create a firm construction translating force in any direction. Figure 4.1 shows: a) forces applied to an inverted catenary AB resting on the ground; b) ground replaced by the equivalent forces; c) a free force at B replaced with the interaction with the second inverted catenary BC connected at the point B, so that the tangent force acting upon AB at B is collinear with the tangent force acting on BC.

Fig. 4.1

As we see, the force in the construction ABC is translated from A to C in the optimal way.

The connected catenaries don't need to be in one plane, but create a complex three-dimensional structure translating the pressure force in any direction.

Probably, the term of "being connected" in Tai Chi refers exactly to the alignment of connected catenaries.

For example in a Push posture (an4), the force-translating chain from palms to the ground is composed of (just to mention the main ones) palm approximating catenoids, arm approximating inverted catenary, shoulder joints approximating dome-like catenoids (sometimes to correct shoulder position they suggest to imagine that one gently holds a couple of raw eggs under armpits), inverted catenary connecting two shoulders, then backbone with the top of its curve at Ming Men point, hip joints, etc down to soles.

5 Feeling of catenary and getting connected

This section has to be more subjective for two reasons:

• By no means, I claim to be a Tai Chi master and the application of the catenary logic to my own practice may be less than mature. It may be not only a weakness, but also a strength of my point: catenary analysis can help even the less advanced students to reflect on their practice.

• On the other hand, Tai Chi is subjective by its nature, as it connects the reality of physical interaction between bodies (i.e. interaction in terms of forces, energy, resistance of materials, etc) with the mental image of our bodies, movements, intentions, etc.

I found that there is a very distinctive feeling in my body, when a chain of bones connected by tendons is "hanging" between two points of the force application. (Say, my armpit or elbow cave get a sort of tingling sensation of being emptied, unloaded and so felt my backbone, too.) It was a feeling of a sail full of wind or a tent sagging under the weight of rain water.

There are two extreme points of each catenary, the points of force application. Between them everything should be relaxed to let the curve naturally get shaped under the action of the force. The two extreme points are the points beyond which we cannot continue the same curve and therefore need to connect it to the next curve. E.g. wrist joint and shoulder joint will be such points in Push (an4), as the curve of arm cannot be continued  with the curve of the rounded shoulder line. These two curves need to be connected with the catenoid-like armpit cave.

Thus, in my practice, when I get some force (gravity or an opponent's push) applied at two points (say A and B) for each limb or sequence of the bones affected by a force, I try to identify the sequence of catenaries translating force between A and B. For each catenary, I try to figure out its extreme points (where the force will be translated from this catenary to the next, say C and D). Then, I try to relax as much as possible all between C and D. I apply this procedure to each catenary or catenoid in the chain. Once done, I feel that my  posture is corrected.

6 Conclusion

Catenary seems to give us a generalized physical picture that could make us more comfortable with the notions of Gua (Kwa) and being connected and give us a tool of formalized description of some physical aspects of Tai Chi, as well as a tool for Tai Chi practice.

References

(1) Paul Brecher, The Kwa - http://www.taichiamerica.com/kwa.htm

(2) Catenary - http://en.wikipedia.org/wiki/Catenary(***)

(3) Arch - http://en.wikipedia.org/wiki/Arch

(4) William C. C. Chen, The Mechanics of Three Nails - http://www.williamccchen.com/3nails.htm

(5) Eric Mead, How to teach and train relaxation - a forum entry on AikiWeb: www.aikiweb.com/forums/printthread.php?t=11449&page=3&pp=25

Notes

(*) Recently, in an Aikido forum, I found the entry by Eric Mead that contains identical ideas about the connection between relaxation and catenary applied to Aikido (see 5).

(**) I would highly appreciate if anyone could confirm if this reasoning makes sense.

(***) It's often said that references to Wikipedia cannot be considered as a firm evidence (as this source is not "scientific" enough), however you can find the same information about catenary in any first-year university textbook on mechanics. I refer to Wikipedia, just because it is so easily accessible.

 Vsevolod Vlaskine

2006

Contents

Tai Chi postures and catenary curve © Vsevolod Vlaskine 2006