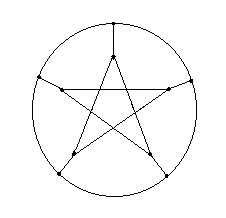
A snark is known in the math world as a non-planar, trivalent, non-Tait-colourable graph. It looks kinda like this:

It's actually called a Petersen graph, until Martin Garnder gave it this more playful title in a 1976 issue of Scientific American. You wouldn't think so to look at it, but you can serve it with greens and it's handy for striking a light. It was also thought to have some use in solving the Four-Colour Problem. You see, there is a parallel between colouring the edges and the regions of a graph, for which a proof exists somewhere. What do you expect? I am not a math major. Some people figured out that if you could find a planar version of the snark (where the only places lines intersect is at vertices), then you could prove that there existed at least one graph that required more than four colours. The Petersen graph, you see, requires four colours for its edges (translating to five for its regions):

Fortunately, the Four-Colour Theorem has been proven, so no Boojums exist, and we are all safe. Try telling that to the Baker.
It also happens that a Snark is the mythical beastie that figures in Lewis Carroll's poem The Hunting of the Snark.
Frankly, I don't know. Probably something. Send me your hypotheses.
© 1997 cosmobimbo@hotmail.com