Chaos

Manifestations du chaos

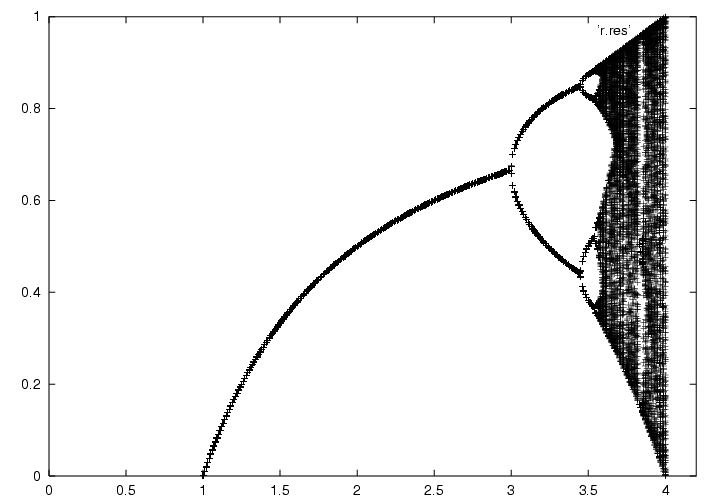
Ce graphique représente la population finale pour différents paramètre de croissance. Sur l'axe des x (axe horizontal), nous avons la valeur du paramètre de croissance, tandis que sur l'axe des y (axe vertical), nous avons la valeur finale de la population après 1000 itérations de l'équation suivante :

X(n+1)=R*X(n)*(1-X(n))

Figure 1

Ainsi, on prends par exemple un X(n) initial de 0,4. On substitue cette valeur dans l'équation pour obtenir X(n+1). Avec cette nouvelle valeur, on la substitue dans l'équation pour obtenir X(n+2) et ainsi de suite, jusqu'à X(1000) dans cette étude-ci. Après un nombre quelconque d'itération, l'équation se stabilise et on obtient une valeur stable. Cette valeur stable et constante est ensuite inscrite sur la figure 1.

Par exemple, pour un R=2,7 on obtient une population de 0,6292 (zéro représente l'extinction et 1 représente la plus grande population imaginable pour un environnement quelconque).

Ainsi on remarque plusieurs choses intéressantes. Tout d'abord, pour des valeurs faibles du paramètre R, l'extinction est presque assurée. Ce qui ne cause pas de surprise. Le plus étonnant est ce qui vient aux alentours de R=3. À partir de ce moment, la population finale oscille entre 2 valeurs distinctes et assez éloignées. Le chaos embarque tranquillement, mais n'est pas encore présent.

Un peu plus loin, il y a quatres valeurs possibles et tout de suite après c'est le chaos à proprement parlé. La population finale prends pratiquement n'importe quelle valeur et ce, sans périodicité apparente.

Si on regarde bien, on remarqueras une zone de stabilité à l'intérieur même du chaos. Entre 3,62 et 3,64 on obtient miraculeusement une zone bien nette de stabilité où la population oscille entre 6 valeurs seulement.

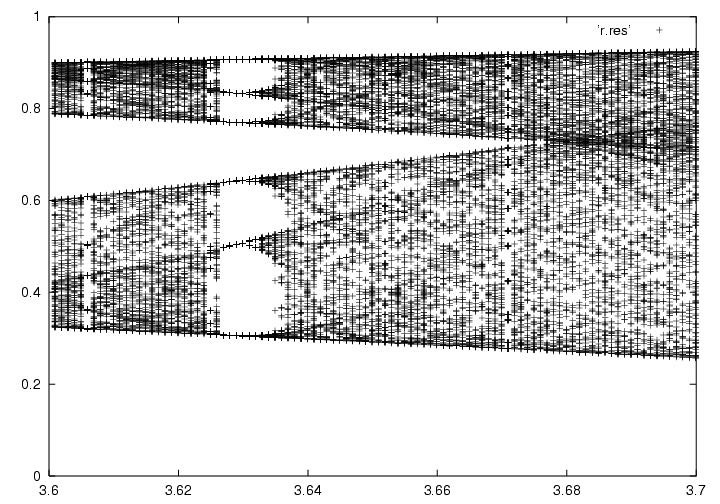
Figure 2 : Agrandissement de la figure 1

Agrandissons encore l'image et centrons celle-ci autour de 3,8 à 3,9. Regarder sur la figure 3. On remarque que nous obtenons un système avec une période 3. James Yorke, un mathématicien, a démontré qu'un système avec une période 3 était nécessairement chaotique dans son article "Preiod three implies chaos¨.

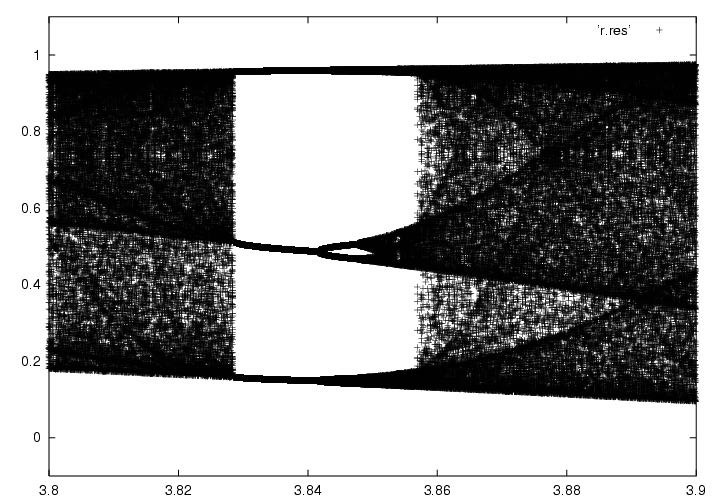
Figure 3 : système chaotique avec une période 3.

J'aimerais amener votre attention sur l'invariance d'échelle. Sur la figure précédente et sur la figure suivante, on remarque que la même structure revient. C'est une manifestation de l'invariance d'échelle que l'on retrouve aussi dans les fractales ainsi que dans la théorie unificatrice de Laurent Nottale, "La théorie des échelles". La même structure se répète sans cesse, peu importe l'échelle à laquelle on regarde. Fait à noter, les 4 figures ont été prise à partir du même programme, seul l'échelle à été modifié pour pouvoir obtenir un zoom intéressant.

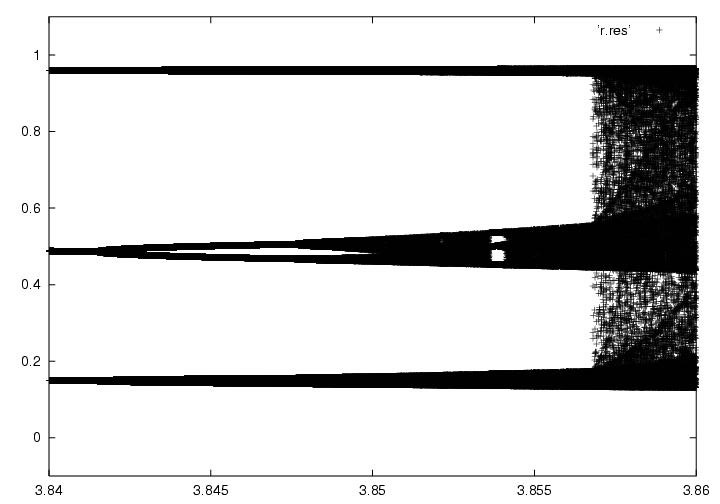
Figure 4 : Invariance d'échelle.

Étrange et remarquable comme nous pouvons toucher au chaos avec une équation toute simple, mais qui donne des résultats assez complexes.

Je mets ici en annexe, le programme Fortran que j'ai écrit pour réaliser cette étude.

Code Fortran

Retour à la page principale