1.- Conforme a la descripción que se da
en el enunciado del problema, sólo pueden aparecer tres fases sólidas
en el diagrama: los metales puros A y B que son mutuamente insolubles y
el compuesto C.
La existencia de dos puntos singulares en la línea
de liquidus indica que se dan dos reacciones entre tres fases en el sistema
que se considera. La primera de ellas es una transformación peritéctica
que se produce a 600°C ("... ambos metales forman un compuesto definido
C cuya fusión incongruente a 600°C ...") y la segunda es la
solidificación de un eutéctico ("... el microconstituyente
bifásico ...") a 300°C según muestra el tramo isotérmico
que aparece en la curva t-T de la aleación con el 10% de B.
El único diagrama que cumple con todas las
condiciones que se fijan en el enunciado es el que se muestra a continuación.
Para completar la definición del diagrama es necesario determinar
las coordenadas de los puntos E, Q y P.

 La composición del eutéctico se puede
calcular a partir del segundo párrafo del enunciado que permite
evaluar la composición que corresponde a uno de los puntos de la
línea de liquidus a 400°C:
La composición del eutéctico se puede
calcular a partir del segundo párrafo del enunciado que permite
evaluar la composición que corresponde a uno de los puntos de la
línea de liquidus a 400°C:

El porcentaje de A sólido a 400°C resulta
ser:

mientras que la cantidad de A que contiene el líquido
en equilibrio es:
Cantidad de A en L = % de L en la aleación x % de A en L / 100 =

De lo anterior se llega a:

Como, según se indica en la línea
anterior a las preguntas, las líneas del diagrama deben ser rectas,
el %B en el eutéctico resulta ser del 30 como se puede ver en la
construcción gráfica que se muestra a continuación:

A partir de los datos del tercer párrafo
relativos a la aleación del 50% en B, se puede calcular la composición
química del compuesto definido C:


Cantidad de C en el eutéctico = masa del eutéctico x %C en
E / 100 =

C libre = 17,5 + Cantidad de C en el eutéctico Þ

Una vez que se conoce la composición del
compuesto C, la del punto Q se puede calcular a partir de los datos referentes
a la fusión de C que se recogen en el primer párrafo:


2.- La solidificación de la aleación
con el 60% de B comienza a 640°C. A esta temperatura comienzan a separarse
cristales de metal B a partir del líquido cuya composición
tiende a acercarse a del punto Q. Justo por encima de los 600°C, la
cantidad de B que ha solidificado es:

A 600°C se forma el compuesto C por una reacción
peritéctica. Las fases presentes al finalizar esta reacción
son líquido con un 50% de B y compuesto C en cantidad de:

Por debajo de 600°C, continua la solidificación
del compuesto mientras el líquido se empobrece en B y su composición
se aproxima a la del eutéctico, composición que alcanza a
los 300°C. Justo por encima de esa temperatura la cantidad de C que
se ha formado es:

La temperatura se mantiene constante mientras que
el líquido con el 30% de B solidifica. Al finalizar este proceso,
la estructura de la aleación está formada por C proeutéctico
y eutéctico A-C. La cantidad de fase C, tanto eutéctica como
proeutéctica, presente es:

Todos los resultados anteriores se resumen en las
gráficas que se presentan a continuación:

3.- Aleaciones hipoeutécticas: la estructura
estará formada por granos oscurecidos de metal A que tienden a aparecer
como constituyente disperso y eutéctico como constituyente matriz
(estructura 1).
Aleación de composición eutéctica:
granos formados por láminas alternadas de metal A y compuesto C.
Tras el ataque, las láminas de A aparecen coloreadas mientras las
de C se ven claras (estructura 2).
Aleación hipereutéctica: granos claros
de C proeutéctico como constituyente disperso y eutéctico
como constituyente matriz (estructura 3).
Aleación con %B > 80: granos oscurecidos de
metal B contorneados por una matriz clara de compuesto C (estructura 4).

4.-

De acuerdo con la figura anterior,
las fases que coexisten a la temperatura T son metal A sólido y
líquido con una composición:

La cantidad de metal A libre en la aleación del X% de B es:

y la disuelta en el líquido es:
Cantidad de A en L = % de L en la aleación x % de A en L / 100 =

De la condición del enunciado se sigue:

y, tras sustituir L por su valor en función de T y despejar, resulta:

5.- A partir de la expresión [1] del apartado
anterior se llega a:

que se hace máxima cuando L es máxima,
es decir, cuando T = TE y L = E. El valor
extremo de m resulta ser:

Para la aleación del 10% de B se tiene:
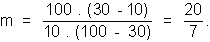
Volver al menú





![]()
![]()


![]()
![]()
![]()

![]()



![]()
![]()
![]()
![]()