En la sopa primordial que puse recientemente a fuego lento en mí ordenador, los glovitos que no acertaban a
atinar en sus predicciones se extinguían. Los más acertados dejaban progenie, la cual lograría a veces mejorar
el índice de acierto de sus ancestros. Al cabo, terminó por producirse evolutivamente una estirpe de individuos capaces de predicción perfecta.
Los glovitos y sus tendencias evolutivas ilustran con gran pulcritud una
forma de programación conocida como
algoritmo genético. Esta técnica, de
la que fue pionero hará unos veinte
años John H. Holland, de la Universidad de Michigan, permite en ocasiones
resolver difíciles problemas, por obtención evolutiva de una sucesión de soluciones aproximadas. Emparejando
unas con otras las mejores con las antiguas soluciones se obtienen soluciones
aproximadas nuevas. No tarda mucho
en aparecer una solución mejor que sus
progenitoras, que pasa a encuadrarse
entre las reproductoras preferentes. Se
han aplicado con cierto buen éxito algoritmos genéticos al reconocimiento de
formas y patrones, a sistemas clasificadores, al funcionamiento de oleoductos, al diseño y distrihución de símbolos y a unos pocos problemas más. En
mi sopa computarizada. esta técnica
produjo una estirpe de glovitos de comportamiento superior. ¿Se debió tal
éxito a la eficacia general de) método
de algoritmo genético. o a la simplicidad de la tarea de predicción que debían afrontar los glovitos? Resulta dificil responder a esta pregunta. Los lectores interesados pueden reflexionar
sobre ella y. si tienen a su alcance un
ordenador, reproducir el fenómeno subyacente.
Un autómata finito puede encontrarse en un número de estados;
la recepción de una señal de entrada lo
hace pasar automaticamente de un estado a otro. La clase de autómatas utilizados en los glovitos también generan
señales. En el seno del autómata, las
señales recibidas se representan por
símbolos. Cuando se recibe una señal,
el autómata cambia de estado y emite
una segunda señal.
Para representar el proceso tesulta
adecuada una tabla de transiciones de
estados. Por ejemplo, un autómata que pueda adoptar tres estados, A, B y C
y sea capaz de manejar unos y ceros
aferenles y eferentes, queda pulcramente representado por una tabla de 3 por 4. Para cada estado en que
el autómata pueda encontrarse, y para
cada símbolo que pueda rccibir, la tabla dispone de dos entradas. La primera da el correspondiente simbolo, de
salida, la segunda, el estado que el autómata va a adoptar a continuación
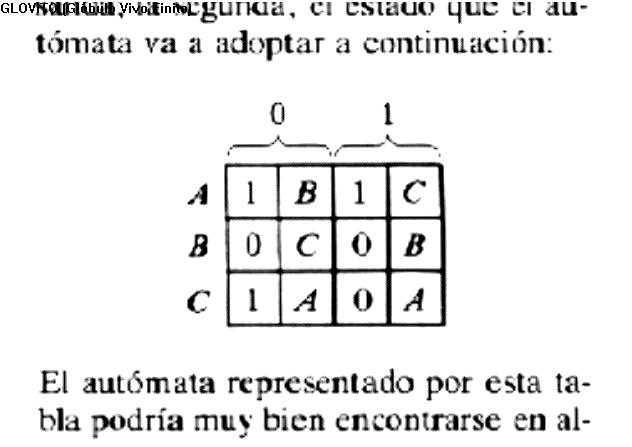El autómata representado por esta tabla podría muy hien encontrarse en algún instante en el estado C. Si el autómata recibiera entonces un 1, la tabla diría que el autómata generaría un
0 y pasaría a adoptar el estado A.
Otra representación que los humanos encuentran más fácil de leer, es el
diagrama sagital de transición de estados.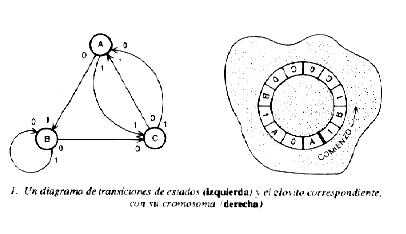 
En él los círculos representan estados y las flechas transiciones. Para
denotar que un autómata pasa de un
estado a otro cuando recibe un símbolo
específico, se traza una flecha que vaya
de uno, a otro, La flecha debe ir rotulada tanto con el simbolo de entrada,
causante de la transición. como con el
simbolo de salida resultante.
Los autómatas finitos comienzan a
funcionar partiendo siempre de un estado específico, llamado inicial. Cada
vez que un imaginario reloj da un golpe
de péndulo, llega un nuevo símbolo, se
emíte otro nuevo símbolo y se adopta
un nuevo estado. Los autómatas que he
utilizado para mis glovitos reciben y envían todos dos únicos simbolos, siempre los mismos: 0 y 1. ¿Cómo ha de interpretarse el com.
portamiento de los glovitos, si tan poco
se conoce de la biología de esas criaturas? En ello precisamente reside el
placer de la abstracción. Los símbolos recibidos por el autómata son meros
mensajes sensorios (percepciones) procedentes del entorno. Correlativamente, un símbolo de salida puede entenderse por la respuesta que el organismo da al estado
más reciente de su ambiente.
Tan versátil es la noción de glovito,
que sus entradas y salidas pueden representar gran diversidad de fenómenos biológicos específicos. Por ejemplo, una señal de entrada podría representar un gradiente térmico o químico. El correspondiente símbolo de salida podría ser una orden dirigída a un efector que controlase las vibraciones de cilios, o que tuviera a su cargo un mecanismo de esporulación. Una tarea
que reviste gran importancia para todo
ser vivo que desee evolucionar hasta un nivel minimamente aceptable (catedrático de universidad, pongarnos por
caso) es es la predicción de los cambios de su entorno. Para los glovitos, su ambiente vital consiste en una secuencia,
aparentemente interminable, de signos
0 y 1. En la medida en que los símbolos
recibidos sean indicativos de acontecimientos importantes, comportará sin
duda cierta ventaja que el glovito tenga
capacidad de predecir cuál será el proximo simbolo, y tanto más si en alguna
interpretación específica del funcionamiento del glovito se vieran reforzadas
sus propias posibilidados de superviviencia. La mayoría de los glovitos son bastante ineptos en lo tocante a predecir
el comportamiento del entorno. Por
ejemplo, el glovito descrito por la tabla
de transiciones dada responde a la secuencia de señales ambientales
0111000010110...
con las salidas
10000011001000.......
En cada etapa de su funcionamiento, la
salida del glovito es su pronóstico de
cuál será la próxima señal que llegará
procedente del entorno. Para hallar el
número de pronósticos correctos, se
desplaza la secuencia de salida un símbolo hacia la derecha, y se la compara.
bit a bit, con la secuencia de entrada,
Contemos el número de símbolos concordantes. En este caso, el glovito tan
sólo predijo correctamente seis de los
doce símbolos que le fueron llegando,
puntuación no superior a lo que sería
de esperar pronosticando al puro azar.
Es fácil pedir demasiado a los autómatas finitos. En efecto, no hay derecho a exigirle a un glovito que sea capaz de pronosticar correctamente las
señales de medios ambientales. Intentemos reflexionar por un momento sobre esta cuestión. ¿Por qué habrá de
constar toda secuencia correctamente
predicha de una ristra fija de símbolos,
interminablemente repetida? Por
ejemplo, el glovito de tres estados que
antes fracasó en la prueba de predicción que le propusimos, triunfa brillantemente en la siguiente secuencia ambiental:
0100110100110100l1 . . .
Pero aquí la sucesión de valores ambientales desfila al compás de un sencillo redoble, a saher, 010011.
Existen varias docenas de glovitos
triestado, pero tan solo unos pocos son
capaces de predecir correctamenie esta
secuencia. Los glovitos de más de tres
estados con capacidad de predicción
perfecta para una sucesión ambiental
determinada son raros, y escasean
tanto más cuanto mayor es el número
de estados. La predictibilidad depende
fuertemenle del período de la sucesión.
Si la serie fundamental de símbolos es
sufícientemente larga, ningún glovito
número prefijado, n, de estados
conseguirá jamás llegar a pronosticarla
perfectamente. Existe, evidentemente,
una relación entre el número de estados que puede adoptar un glovito y la
máxima longitud del período que es capaz de pronosticar perfectamente. Seguramente los lectores gusten de descubrir por sí mismos tal relación. ¿Cuál
es la máxima longitud de período que
puede pronosticar un glovito de n estados?
Los glovitos son algo más que autómatas finitos que se esfuerzan por predecir su entorno, pues tienen un cromosoma. Por algún procedimiento (que veremos más adelante) los glovitos engendran periódicamente nuevos glovitos. Al examinar el cromosoma del glovito y ponerlo en relación con el automata finito correspondiente, vemos de
qué modo los genes hereditarios determinan el comportamienlo de la progenie. Comencemos con la tabla de transiciones de estados y vayamos separando. una por una, las filas. de arriba
abajo. Unamos las filas, pegando la
cola de cada una con la cabeza de la
siguicnte y, finalmente, el comienzo con
el fin de la tira así obtenida- El resultado será un cromosoma circular.
Antes de llevar a cabo esta última
operación de empalme, el cromosoma
de nuestro ejemplar triestado se nos
presenta como una ristra de 12 genes:
1 B 1 C 0 C 0 B 1 A 0 A
En puridad, los símbolos de esta serie
son alelos. Un alelo es una forma es~
pecífica de gen, que se asienta en un
locus determinado. Los genes pueden
por tanto, especificarse tanto por su
nombre como por su emplazamiento, o
locus. Así pues, el séptimo símbolo,
contando desde la izquierda, controla
el símbolo de salida de un glovito
cuando éste se encuentra en estado B
y se recibe un 1 procedente del en-
torno. Aquí, el locus es 7.
Hace poco preparé en mi ordenador
personal una sopa primordial, con 10
glovitos tetraestado. No habían transcurrido 1000 de las unidades de tiempo.
que llamo cronones, cuado ninguno de
los glovitos originales permanecía con
vida. Todos habían sido remplazados
por otros de mayor habilidad de predicción. La pantalla de mi ordenador
iba mostrando las puntuaciones máxima y minina alcanzadas por la poblacíón existente en ese momento. La
puntuación mínínima fluctuaba fuertemente; la máxima, en cambio, fue trepando poco a poco (véase la figura).
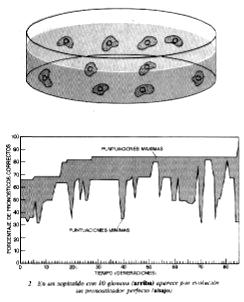Justanente cuando comenzaba yo a desesperar de que pudiera evolucionar un
predictor perfecto apareció uno súbitamente y, a partir de ahi, la puntuacion máxima quedó estancada en 100.
Todo lo cual suscita la cuestión de
cómo evolucionan exactamente los glovitos en mi caldo computarizado. Periódicamente, un rayo cósmico atraviesa la sopa e impacta al azar en un
cromosoma, en un lugar igualmenle
aleatorio. El resultado de ello es que
un gen específico pasa de un alelo a
otro. Por ejeraplo. en el siguiente cromosoma, que pertenece a un glovito de
cuatro estados, el gen sustituido en el locus 3 controla el símbolo de salida correspondientc a la transición desde el
estado A, cuando a la criatura le llega
un 1.
0 D 1 C 0 D 0 B 1 A 0 C 1 B 1 A
Un rayo cósmico impacta en este gen,
y modifica ligeramente su cromosoma:
0 D 0 C 0 D 0 B 1 A 0 C 1 B 1 A
La otra fuente de variación del
acervo génico de los glovitos es el
apareamiento. Durante la estación de
procreación. el glovito de máxima puntuación intercambia genes con otro elegido al azar. La descendencia porta un
cromosoma compuesto. Parte de él
proviene del progenitor superior, la
otra. del ganador en la lotería de apareamiento. La composición se asemeja al fenómeno de entrecruzamiento que
se da en los cromosornas reales. En los
cromosomas de los glovitos. el entrecruzamiento puede ilustrarse combinando el primero de los cromosomas antes mencionados (sin alteración) con
otro
1 A 1 B 0 D 1 A 0 C 1 D 1 B
^ ^
| |
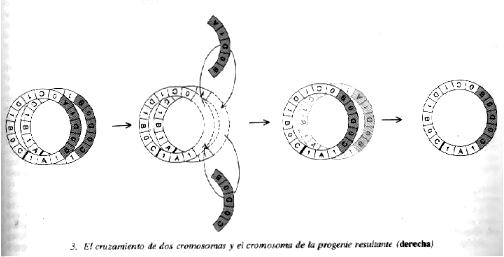
Las flechas indican los puntos de entrecruzamiento, elegidos de forma estocástica. El eromosoma descendiente es
idéntico al del segundo progenitor
hasta llegar al primer punto de cruzamiento. Entre dicho punto y el segundo
es idéntico a la correspondiente porción del cromosoma del primero. Tras
el segundo punto es nuevamente idéntico al cromosoma del segundo progenitor (véase la figura 3)
1A1CODOB0C1D1B0C
Antes de decidirine a redactar y poner a prueba el programa primordial
era yo un tanto escéptico acerca del va
lor del apareamiento por cruce. Descubrí con sorpresa, sin embargo, que si
el primer progenitor es razonablemente acertado en sus pronósticos, la
descendencia tiende a serlo también.
Los lectores pueden juzgar por si
mismos preparando un programa que
llamaremos AUTOSOPA.
Al listarlo el
programa no excede demasiado de una
página.
Se
han aplicado con cierto buen éxito algoritmos genéticos al reconocimiento de
formas y patrones, a sistemas clasificadores, al funcionamiento de oleoductos, al diseño y distrihución de símbolos y a unos pocos problemas más. En
mi sopa computarizada. esta técnica
produjo una estirpe de glovitos de comportamiento superior. ¿Se debió tal
éxito a la eficacia general de) método
de algoritmo genético. o a la simplicidad de la tarea de predicción que debían afrontar los glovitos? Resulta dificil responder a esta pregunta. Los lectores interesados pueden reflexionar
sobre ella y. si tienen a su alcance un
ordenador, reproducir el fenómeno subyacente.
Un autómata finito puede encontrarse en un número de estados;
la recepción de una señal de entrada lo
hace pasar automaticamente de un estado a otro. La clase de autómatas utilizados en los glovitos también generan
señales. En el seno del autómata, las
señales recibidas se representan por
símbolos. Cuando se recibe una señal,
el autómata cambia de estado y emite
una segunda señal.
Para representar el proceso tesulta
adecuada una tabla de transiciones de
estados. Por ejemplo, un autómata que pueda adoptar tres estados, A, B y C
y sea capaz de manejar unos y ceros
aferenles y eferentes, queda pulcramente representado por una tabla de 3 por 4. Para cada estado en que
el autómata pueda encontrarse, y para
cada símbolo que pueda rccibir, la tabla dispone de dos entradas. La primera da el correspondiente simbolo, de
salida, la segunda, el estado que el autómata va a adoptar a continuación
El autómata representado por esta tabla podría muy hien encontrarse en algún instante en el estado C. Si el autómata recibiera entonces un 1, la tabla diría que el autómata generaría un
0 y pasaría a adoptar el estado A.
Otra representación que los humanos encuentran más fácil de leer, es el
diagrama sagital de transición de estados. En él los círculos representan estados y las flechas transiciones. Para
denotar que un autómata pasa de un
estado a otro cuando recibe un símbolo
específico, se traza una flecha que vaya
de uno, a otro, La flecha debe ir rotulada tanto con el simbolo de entrada,
causante de la transición. como con el
simbolo de salida resultante.
Los autómatas finitos comienzan a
funcionar partiendo siempre de un estado específico, llamado inicial. Cada
vez que un imaginario reloj da un golpe
de péndulo, llega un nuevo símbolo, se
emíte otro nuevo símbolo y se adopta
un nuevo estado. Los autómatas que he
utilizado para mis glovitos reciben y envían todos dos únicos simbolos, siempre los mismos: 0 y 1. ¿Cómo ha de interpretarse el com.
portamiento de los glovitos, si tan poco
se conoce de la biología de esas criaturas? En ello precisamente reside el
placer de la abstracción. Los símbolos recibidos por el autómata son meros
mensajes sensorios (percepciones) procedentes del entorno. Correlativamente, un símbolo de salida puede entenderse por la respuesta que el organismo da al estado
más reciente de su ambiente.
Tan versátil es la noción de glovito,
que sus entradas y salidas pueden representar gran diversidad de fenómenos biológicos específicos. Por ejemplo, una señal de entrada podría representar un gradiente térmico o químico. El correspondiente símbolo de salida podría ser una orden dirigída a un efector que controlase las vibraciones de cilios, o que tuviera a su cargo un mecanismo de esporulación. Una tarea
que reviste gran importancia para todo
ser vivo que desee evolucionar hasta un nivel minimamente aceptable (catedrático de universidad, pongarnos por
caso) es es la predicción de los cambios de su entorno. Para los glovitos, su ambiente vital consiste en una secuencia,
aparentemente interminable, de signos
0 y 1. En la medida en que los símbolos
recibidos sean indicativos de acontecimientos importantes, comportará sin
duda cierta ventaja que el glovito tenga
capacidad de predecir cuál será el proximo simbolo, y tanto más si en alguna
interpretación específica del funcionamiento del glovito se vieran reforzadas
sus propias posibilidados de superviviencia. La mayoría de los glovitos son bastante ineptos en lo tocante a predecir
el comportamiento del entorno. Por
ejemplo, el glovito descrito por la tabla
de transiciones dada responde a la secuencia de señales ambientales
0111000010110...
con las salidas
10000011001000.......
En cada etapa de su funcionamiento, la
salida del glovito es su pronóstico de
cuál será la próxima señal que llegará
procedente del entorno. Para hallar el
número de pronósticos correctos, se
desplaza la secuencia de salida un símbolo hacia la derecha, y se la compara.
bit a bit, con la secuencia de entrada,
Contemos el número de símbolos concordantes. En este caso, el glovito tan
sólo predijo correctamente seis de los
doce símbolos que le fueron llegando,
puntuación no superior a lo que sería
de esperar pronosticando al puro azar.
Es fácil pedir demasiado a los autómatas finitos. En efecto, no hay derecho a exigirle a un glovito que sea capaz de pronosticar correctamente las
señales de medios ambientales. Intentemos reflexionar por un momento sobre esta cuestión. ¿Por qué habrá de
constar toda secuencia correctamente
predicha de una ristra fija de símbolos,
interminablemente repetida? Por
ejemplo, el glovito de tres estados que
antes fracasó en la prueba de predicción que le propusimos, triunfa brillantemente en la siguiente secuencia ambiental:
0100110100110100l1 . . .
Pero aquí la sucesión de valores ambientales desfila al compás de un sencillo redoble, a saher, 010011.
Existen varias docenas de glovitos
triestado, pero tan solo unos pocos son
capaces de predecir correctamenie esta
secuencia. Los glovitos de más de tres
estados con capacidad de predicción
perfecta para una sucesión ambiental
determinada son raros, y escasean
tanto más cuanto mayor es el número
de estados. La predictibilidad depende
fuertemenle del período de la sucesión.
Si la serie fundamental de símbolos es
sufícientemente larga, ningún glovito
número prefijado, n, de estados
conseguirá jamás llegar a pronosticarla
perfectamente. Existe, evidentemente,
una relación entre el número de estados que puede adoptar un glovito y la
máxima longitud del período que es capaz de pronosticar perfectamente. Seguramente los lectores gusten de descubrir por sí mismos tal relación. ¿Cuál
es la máxima longitud de período que
puede pronosticar un glovito de n estados?
Los glovitos son algo más que autómatas finitos que se esfuerzan por predecir su entorno, pues tienen un cromosoma. Por algún procedimiento (que veremos más adelante) los glovitos engendran periódicamente nuevos glovitos. Al examinar el cromosoma del glovito y ponerlo en relación con el automata finito correspondiente, vemos de
qué modo los genes hereditarios determinan el comportamienlo de la progenie. Comencemos con la tabla de transiciones de estados y vayamos separando. una por una, las filas. de arriba
abajo. Unamos las filas, pegando la
cola de cada una con la cabeza de la
siguicnte y, finalmente, el comienzo con
el fin de la tira así obtenida- El resultado será un cromosoma circular.
Antes de llevar a cabo esta última
operación de empalme, el cromosoma
de nuestro ejemplar triestado se nos
presenta como una ristra de 12 genes:
1 B 1 C 0 C 0 B 1 A 0 A
En puridad, los símbolos de esta serie
son alelos. Un alelo es una forma es~
pecífica de gen, que se asienta en un
locus determinado. Los genes pueden
por tanto, especificarse tanto por su
nombre como por su emplazamiento, o
locus. Así pues, el séptimo símbolo,
contando desde la izquierda, controla
el símbolo de salida de un glovito
cuando éste se encuentra en estado B
y se recibe un 1 procedente del en-
torno. Aquí, el locus es 7.
Hace poco preparé en mi ordenador
personal una sopa primordial, con 10
glovitos tetraestado. No habían transcurrido 1000 de las unidades de tiempo.
que llamo cronones, cuado ninguno de
los glovitos originales permanecía con
vida. Todos habían sido remplazados
por otros de mayor habilidad de predicción. La pantalla de mi ordenador
iba mostrando las puntuaciones máxima y minina alcanzadas por la poblacíón existente en ese momento. La
puntuación mínínima fluctuaba fuertemente; la máxima, en cambio, fue trepando poco a poco (véase la figura).
Justanente cuando comenzaba yo a desesperar de que pudiera evolucionar un
predictor perfecto apareció uno súbitamente y, a partir de ahi, la puntuacion máxima quedó estancada en 100.
Todo lo cual suscita la cuestión de
cómo evolucionan exactamente los glovitos en mi caldo computarizado. Periódicamente, un rayo cósmico atraviesa la sopa e impacta al azar en un
cromosoma, en un lugar igualmenle
aleatorio. El resultado de ello es que
un gen específico pasa de un alelo a
otro. Por ejeraplo. en el siguiente cromosoma, que pertenece a un glovito de
cuatro estados, el gen sustituido en el locus 3 controla el símbolo de salida correspondientc a la transición desde el
estado A, cuando a la criatura le llega
un 1.
0 D 1 C 0 D 0 B 1 A 0 C 1 B 1 A
Un rayo cósmico impacta en este gen,
y modifica ligeramente su cromosoma:
0 D 0 C 0 D 0 B 1 A 0 C 1 B 1 A
La otra fuente de variación del
acervo génico de los glovitos es el
apareamiento. Durante la estación de
procreación. el glovito de máxima puntuación intercambia genes con otro elegido al azar. La descendencia porta un
cromosoma compuesto. Parte de él
proviene del progenitor superior, la
otra. del ganador en la lotería de apareamiento. La composición se asemeja al fenómeno de entrecruzamiento que
se da en los cromosornas reales. En los
cromosomas de los glovitos. el entrecruzamiento puede ilustrarse combinando el primero de los cromosomas antes mencionados (sin alteración) con
otro
1 A 1 B 0 D 1 A 0 C 1 D 1 B
^ ^
| |
Las flechas indican los puntos de entrecruzamiento, elegidos de forma estocástica. El eromosoma descendiente es
idéntico al del segundo progenitor
hasta llegar al primer punto de cruzamiento. Entre dicho punto y el segundo
es idéntico a la correspondiente porción del cromosoma del primero. Tras
el segundo punto es nuevamente idéntico al cromosoma del segundo progenitor (véase la figura 3)
1A1CODOB0C1D1B0C
Antes de decidirine a redactar y poner a prueba el programa primordial
era yo un tanto escéptico acerca del va
lor del apareamiento por cruce. Descubrí con sorpresa, sin embargo, que si
el primer progenitor es razonablemente acertado en sus pronósticos, la
descendencia tiende a serlo también.
Los lectores pueden juzgar por si
mismos preparando un programa que
llamaremos AUTOSOPA.
Al listarlo el
programa no excede demasiado de una
página.
Para representar el proceso tesulta
adecuada una tabla de transiciones de
estados. Por ejemplo, un autómata que pueda adoptar tres estados, A, B y C
y sea capaz de manejar unos y ceros
aferenles y eferentes, queda pulcramente representado por una tabla de 3 por 4. Para cada estado en que
el autómata pueda encontrarse, y para
cada símbolo que pueda rccibir, la tabla dispone de dos entradas. La primera da el correspondiente simbolo, de
salida, la segunda, el estado que el autómata va a adoptar a continuación
El autómata representado por esta tabla podría muy hien encontrarse en algún instante en el estado C. Si el autómata recibiera entonces un 1, la tabla diría que el autómata generaría un
0 y pasaría a adoptar el estado A.
Otra representación que los humanos encuentran más fácil de leer, es el
diagrama sagital de transición de estados. En él los círculos representan estados y las flechas transiciones. Para
denotar que un autómata pasa de un
estado a otro cuando recibe un símbolo
específico, se traza una flecha que vaya
de uno, a otro, La flecha debe ir rotulada tanto con el simbolo de entrada,
causante de la transición. como con el
simbolo de salida resultante.
Los autómatas finitos comienzan a
funcionar partiendo siempre de un estado específico, llamado inicial. Cada
vez que un imaginario reloj da un golpe
de péndulo, llega un nuevo símbolo, se
emíte otro nuevo símbolo y se adopta
un nuevo estado. Los autómatas que he
utilizado para mis glovitos reciben y envían todos dos únicos simbolos, siempre los mismos: 0 y 1. ¿Cómo ha de interpretarse el com.
portamiento de los glovitos, si tan poco
se conoce de la biología de esas criaturas? En ello precisamente reside el
placer de la abstracción. Los símbolos recibidos por el autómata son meros
mensajes sensorios (percepciones) procedentes del entorno. Correlativamente, un símbolo de salida puede entenderse por la respuesta que el organismo da al estado
más reciente de su ambiente.
Tan versátil es la noción de glovito,
que sus entradas y salidas pueden representar gran diversidad de fenómenos biológicos específicos. Por ejemplo, una señal de entrada podría representar un gradiente térmico o químico. El correspondiente símbolo de salida podría ser una orden dirigída a un efector que controlase las vibraciones de cilios, o que tuviera a su cargo un mecanismo de esporulación. Una tarea
que reviste gran importancia para todo
ser vivo que desee evolucionar hasta un nivel minimamente aceptable (catedrático de universidad, pongarnos por
caso) es es la predicción de los cambios de su entorno. Para los glovitos, su ambiente vital consiste en una secuencia,
aparentemente interminable, de signos
0 y 1. En la medida en que los símbolos
recibidos sean indicativos de acontecimientos importantes, comportará sin
duda cierta ventaja que el glovito tenga
capacidad de predecir cuál será el proximo simbolo, y tanto más si en alguna
interpretación específica del funcionamiento del glovito se vieran reforzadas
sus propias posibilidados de superviviencia. La mayoría de los glovitos son bastante ineptos en lo tocante a predecir
el comportamiento del entorno. Por
ejemplo, el glovito descrito por la tabla
de transiciones dada responde a la secuencia de señales ambientales
0111000010110...
con las salidas
10000011001000.......
En cada etapa de su funcionamiento, la
salida del glovito es su pronóstico de
cuál será la próxima señal que llegará
procedente del entorno. Para hallar el
número de pronósticos correctos, se
desplaza la secuencia de salida un símbolo hacia la derecha, y se la compara.
bit a bit, con la secuencia de entrada,
Contemos el número de símbolos concordantes. En este caso, el glovito tan
sólo predijo correctamente seis de los
doce símbolos que le fueron llegando,
puntuación no superior a lo que sería
de esperar pronosticando al puro azar.
Es fácil pedir demasiado a los autómatas finitos. En efecto, no hay derecho a exigirle a un glovito que sea capaz de pronosticar correctamente las
señales de medios ambientales. Intentemos reflexionar por un momento sobre esta cuestión. ¿Por qué habrá de
constar toda secuencia correctamente
predicha de una ristra fija de símbolos,
interminablemente repetida? Por
ejemplo, el glovito de tres estados que
antes fracasó en la prueba de predicción que le propusimos, triunfa brillantemente en la siguiente secuencia ambiental:
0100110100110100l1 . . .
Pero aquí la sucesión de valores ambientales desfila al compás de un sencillo redoble, a saher, 010011.
Existen varias docenas de glovitos
triestado, pero tan solo unos pocos son
capaces de predecir correctamenie esta
secuencia. Los glovitos de más de tres
estados con capacidad de predicción
perfecta para una sucesión ambiental
determinada son raros, y escasean
tanto más cuanto mayor es el número
de estados. La predictibilidad depende
fuertemenle del período de la sucesión.
Si la serie fundamental de símbolos es
sufícientemente larga, ningún glovito
número prefijado, n, de estados
conseguirá jamás llegar a pronosticarla
perfectamente. Existe, evidentemente,
una relación entre el número de estados que puede adoptar un glovito y la
máxima longitud del período que es capaz de pronosticar perfectamente. Seguramente los lectores gusten de descubrir por sí mismos tal relación. ¿Cuál
es la máxima longitud de período que
puede pronosticar un glovito de n estados?
Los glovitos son algo más que autómatas finitos que se esfuerzan por predecir su entorno, pues tienen un cromosoma. Por algún procedimiento (que veremos más adelante) los glovitos engendran periódicamente nuevos glovitos. Al examinar el cromosoma del glovito y ponerlo en relación con el automata finito correspondiente, vemos de
qué modo los genes hereditarios determinan el comportamienlo de la progenie. Comencemos con la tabla de transiciones de estados y vayamos separando. una por una, las filas. de arriba
abajo. Unamos las filas, pegando la
cola de cada una con la cabeza de la
siguicnte y, finalmente, el comienzo con
el fin de la tira así obtenida- El resultado será un cromosoma circular.
Antes de llevar a cabo esta última
operación de empalme, el cromosoma
de nuestro ejemplar triestado se nos
presenta como una ristra de 12 genes:
1 B 1 C 0 C 0 B 1 A 0 A
En puridad, los símbolos de esta serie
son alelos. Un alelo es una forma es~
pecífica de gen, que se asienta en un
locus determinado. Los genes pueden
por tanto, especificarse tanto por su
nombre como por su emplazamiento, o
locus. Así pues, el séptimo símbolo,
contando desde la izquierda, controla
el símbolo de salida de un glovito
cuando éste se encuentra en estado B
y se recibe un 1 procedente del en-
torno. Aquí, el locus es 7.
Hace poco preparé en mi ordenador
personal una sopa primordial, con 10
glovitos tetraestado. No habían transcurrido 1000 de las unidades de tiempo.
que llamo cronones, cuado ninguno de
los glovitos originales permanecía con
vida. Todos habían sido remplazados
por otros de mayor habilidad de predicción. La pantalla de mi ordenador
iba mostrando las puntuaciones máxima y minina alcanzadas por la poblacíón existente en ese momento. La
puntuación mínínima fluctuaba fuertemente; la máxima, en cambio, fue trepando poco a poco (véase la figura).
Justanente cuando comenzaba yo a desesperar de que pudiera evolucionar un
predictor perfecto apareció uno súbitamente y, a partir de ahi, la puntuacion máxima quedó estancada en 100.
Todo lo cual suscita la cuestión de
cómo evolucionan exactamente los glovitos en mi caldo computarizado. Periódicamente, un rayo cósmico atraviesa la sopa e impacta al azar en un
cromosoma, en un lugar igualmenle
aleatorio. El resultado de ello es que
un gen específico pasa de un alelo a
otro. Por ejeraplo. en el siguiente cromosoma, que pertenece a un glovito de
cuatro estados, el gen sustituido en el locus 3 controla el símbolo de salida correspondientc a la transición desde el
estado A, cuando a la criatura le llega
un 1.
0 D 1 C 0 D 0 B 1 A 0 C 1 B 1 A
Un rayo cósmico impacta en este gen,
y modifica ligeramente su cromosoma:
0 D 0 C 0 D 0 B 1 A 0 C 1 B 1 A
La otra fuente de variación del
acervo génico de los glovitos es el
apareamiento. Durante la estación de
procreación. el glovito de máxima puntuación intercambia genes con otro elegido al azar. La descendencia porta un
cromosoma compuesto. Parte de él
proviene del progenitor superior, la
otra. del ganador en la lotería de apareamiento. La composición se asemeja al fenómeno de entrecruzamiento que
se da en los cromosornas reales. En los
cromosomas de los glovitos. el entrecruzamiento puede ilustrarse combinando el primero de los cromosomas antes mencionados (sin alteración) con
otro
1 A 1 B 0 D 1 A 0 C 1 D 1 B
^ ^
| |
Las flechas indican los puntos de entrecruzamiento, elegidos de forma estocástica. El eromosoma descendiente es
idéntico al del segundo progenitor
hasta llegar al primer punto de cruzamiento. Entre dicho punto y el segundo
es idéntico a la correspondiente porción del cromosoma del primero. Tras
el segundo punto es nuevamente idéntico al cromosoma del segundo progenitor (véase la figura 3)
1A1CODOB0C1D1B0C
Antes de decidirine a redactar y poner a prueba el programa primordial
era yo un tanto escéptico acerca del va
lor del apareamiento por cruce. Descubrí con sorpresa, sin embargo, que si
el primer progenitor es razonablemente acertado en sus pronósticos, la
descendencia tiende a serlo también.
Los lectores pueden juzgar por si
mismos preparando un programa que
llamaremos AUTOSOPA.
Al listarlo el
programa no excede demasiado de una
página.
En él los círculos representan estados y las flechas transiciones. Para
denotar que un autómata pasa de un
estado a otro cuando recibe un símbolo
específico, se traza una flecha que vaya
de uno, a otro, La flecha debe ir rotulada tanto con el simbolo de entrada,
causante de la transición. como con el
simbolo de salida resultante.
Los autómatas finitos comienzan a
funcionar partiendo siempre de un estado específico, llamado inicial. Cada
vez que un imaginario reloj da un golpe
de péndulo, llega un nuevo símbolo, se
emíte otro nuevo símbolo y se adopta
un nuevo estado. Los autómatas que he
utilizado para mis glovitos reciben y envían todos dos únicos simbolos, siempre los mismos: 0 y 1. ¿Cómo ha de interpretarse el com.
portamiento de los glovitos, si tan poco
se conoce de la biología de esas criaturas? En ello precisamente reside el
placer de la abstracción. Los símbolos recibidos por el autómata son meros
mensajes sensorios (percepciones) procedentes del entorno. Correlativamente, un símbolo de salida puede entenderse por la respuesta que el organismo da al estado
más reciente de su ambiente.
Tan versátil es la noción de glovito,
que sus entradas y salidas pueden representar gran diversidad de fenómenos biológicos específicos. Por ejemplo, una señal de entrada podría representar un gradiente térmico o químico. El correspondiente símbolo de salida podría ser una orden dirigída a un efector que controlase las vibraciones de cilios, o que tuviera a su cargo un mecanismo de esporulación. Una tarea
que reviste gran importancia para todo
ser vivo que desee evolucionar hasta un nivel minimamente aceptable (catedrático de universidad, pongarnos por
caso) es es la predicción de los cambios de su entorno. Para los glovitos, su ambiente vital consiste en una secuencia,
aparentemente interminable, de signos
0 y 1. En la medida en que los símbolos
recibidos sean indicativos de acontecimientos importantes, comportará sin
duda cierta ventaja que el glovito tenga
capacidad de predecir cuál será el proximo simbolo, y tanto más si en alguna
interpretación específica del funcionamiento del glovito se vieran reforzadas
sus propias posibilidados de superviviencia. La mayoría de los glovitos son bastante ineptos en lo tocante a predecir
el comportamiento del entorno. Por
ejemplo, el glovito descrito por la tabla
de transiciones dada responde a la secuencia de señales ambientales
0111000010110...
con las salidas
10000011001000.......
En cada etapa de su funcionamiento, la
salida del glovito es su pronóstico de
cuál será la próxima señal que llegará
procedente del entorno. Para hallar el
número de pronósticos correctos, se
desplaza la secuencia de salida un símbolo hacia la derecha, y se la compara.
bit a bit, con la secuencia de entrada,
Contemos el número de símbolos concordantes. En este caso, el glovito tan
sólo predijo correctamente seis de los
doce símbolos que le fueron llegando,
puntuación no superior a lo que sería
de esperar pronosticando al puro azar.
Es fácil pedir demasiado a los autómatas finitos. En efecto, no hay derecho a exigirle a un glovito que sea capaz de pronosticar correctamente las
señales de medios ambientales. Intentemos reflexionar por un momento sobre esta cuestión. ¿Por qué habrá de
constar toda secuencia correctamente
predicha de una ristra fija de símbolos,
interminablemente repetida? Por
ejemplo, el glovito de tres estados que
antes fracasó en la prueba de predicción que le propusimos, triunfa brillantemente en la siguiente secuencia ambiental:
0100110100110100l1 . . .
Pero aquí la sucesión de valores ambientales desfila al compás de un sencillo redoble, a saher, 010011.
Existen varias docenas de glovitos
triestado, pero tan solo unos pocos son
capaces de predecir correctamenie esta
secuencia. Los glovitos de más de tres
estados con capacidad de predicción
perfecta para una sucesión ambiental
determinada son raros, y escasean
tanto más cuanto mayor es el número
de estados. La predictibilidad depende
fuertemenle del período de la sucesión.
Si la serie fundamental de símbolos es
sufícientemente larga, ningún glovito
número prefijado, n, de estados
conseguirá jamás llegar a pronosticarla
perfectamente. Existe, evidentemente,
una relación entre el número de estados que puede adoptar un glovito y la
máxima longitud del período que es capaz de pronosticar perfectamente. Seguramente los lectores gusten de descubrir por sí mismos tal relación. ¿Cuál
es la máxima longitud de período que
puede pronosticar un glovito de n estados?
Los glovitos son algo más que autómatas finitos que se esfuerzan por predecir su entorno, pues tienen un cromosoma. Por algún procedimiento (que veremos más adelante) los glovitos engendran periódicamente nuevos glovitos. Al examinar el cromosoma del glovito y ponerlo en relación con el automata finito correspondiente, vemos de
qué modo los genes hereditarios determinan el comportamienlo de la progenie. Comencemos con la tabla de transiciones de estados y vayamos separando. una por una, las filas. de arriba
abajo. Unamos las filas, pegando la
cola de cada una con la cabeza de la
siguicnte y, finalmente, el comienzo con
el fin de la tira así obtenida- El resultado será un cromosoma circular.
Antes de llevar a cabo esta última
operación de empalme, el cromosoma
de nuestro ejemplar triestado se nos
presenta como una ristra de 12 genes:
1 B 1 C 0 C 0 B 1 A 0 A
En puridad, los símbolos de esta serie
son alelos. Un alelo es una forma es~
pecífica de gen, que se asienta en un
locus determinado. Los genes pueden
por tanto, especificarse tanto por su
nombre como por su emplazamiento, o
locus. Así pues, el séptimo símbolo,
contando desde la izquierda, controla
el símbolo de salida de un glovito
cuando éste se encuentra en estado B
y se recibe un 1 procedente del en-
torno. Aquí, el locus es 7.
Hace poco preparé en mi ordenador
personal una sopa primordial, con 10
glovitos tetraestado. No habían transcurrido 1000 de las unidades de tiempo.
que llamo cronones, cuado ninguno de
los glovitos originales permanecía con
vida. Todos habían sido remplazados
por otros de mayor habilidad de predicción. La pantalla de mi ordenador
iba mostrando las puntuaciones máxima y minina alcanzadas por la poblacíón existente en ese momento. La
puntuación mínínima fluctuaba fuertemente; la máxima, en cambio, fue trepando poco a poco (véase la figura).
Justanente cuando comenzaba yo a desesperar de que pudiera evolucionar un
predictor perfecto apareció uno súbitamente y, a partir de ahi, la puntuacion máxima quedó estancada en 100.
Todo lo cual suscita la cuestión de
cómo evolucionan exactamente los glovitos en mi caldo computarizado. Periódicamente, un rayo cósmico atraviesa la sopa e impacta al azar en un
cromosoma, en un lugar igualmenle
aleatorio. El resultado de ello es que
un gen específico pasa de un alelo a
otro. Por ejeraplo. en el siguiente cromosoma, que pertenece a un glovito de
cuatro estados, el gen sustituido en el locus 3 controla el símbolo de salida correspondientc a la transición desde el
estado A, cuando a la criatura le llega
un 1.
0 D 1 C 0 D 0 B 1 A 0 C 1 B 1 A
Un rayo cósmico impacta en este gen,
y modifica ligeramente su cromosoma:
0 D 0 C 0 D 0 B 1 A 0 C 1 B 1 A
La otra fuente de variación del
acervo génico de los glovitos es el
apareamiento. Durante la estación de
procreación. el glovito de máxima puntuación intercambia genes con otro elegido al azar. La descendencia porta un
cromosoma compuesto. Parte de él
proviene del progenitor superior, la
otra. del ganador en la lotería de apareamiento. La composición se asemeja al fenómeno de entrecruzamiento que
se da en los cromosornas reales. En los
cromosomas de los glovitos. el entrecruzamiento puede ilustrarse combinando el primero de los cromosomas antes mencionados (sin alteración) con
otro
1 A 1 B 0 D 1 A 0 C 1 D 1 B
^ ^
| |
Las flechas indican los puntos de entrecruzamiento, elegidos de forma estocástica. El eromosoma descendiente es
idéntico al del segundo progenitor
hasta llegar al primer punto de cruzamiento. Entre dicho punto y el segundo
es idéntico a la correspondiente porción del cromosoma del primero. Tras
el segundo punto es nuevamente idéntico al cromosoma del segundo progenitor (véase la figura 3)
1A1CODOB0C1D1B0C
Antes de decidirine a redactar y poner a prueba el programa primordial
era yo un tanto escéptico acerca del va
lor del apareamiento por cruce. Descubrí con sorpresa, sin embargo, que si
el primer progenitor es razonablemente acertado en sus pronósticos, la
descendencia tiende a serlo también.
Los lectores pueden juzgar por si
mismos preparando un programa que
llamaremos AUTOSOPA.
Al listarlo el
programa no excede demasiado de una
página.
Tan versátil es la noción de glovito,
que sus entradas y salidas pueden representar gran diversidad de fenómenos biológicos específicos. Por ejemplo, una señal de entrada podría representar un gradiente térmico o químico. El correspondiente símbolo de salida podría ser una orden dirigída a un efector que controlase las vibraciones de cilios, o que tuviera a su cargo un mecanismo de esporulación. Una tarea
que reviste gran importancia para todo
ser vivo que desee evolucionar hasta un nivel minimamente aceptable (catedrático de universidad, pongarnos por
caso) es es la predicción de los cambios de su entorno. Para los glovitos, su ambiente vital consiste en una secuencia,
aparentemente interminable, de signos
0 y 1. En la medida en que los símbolos
recibidos sean indicativos de acontecimientos importantes, comportará sin
duda cierta ventaja que el glovito tenga
capacidad de predecir cuál será el proximo simbolo, y tanto más si en alguna
interpretación específica del funcionamiento del glovito se vieran reforzadas
sus propias posibilidados de superviviencia. La mayoría de los glovitos son bastante ineptos en lo tocante a predecir
el comportamiento del entorno. Por
ejemplo, el glovito descrito por la tabla
de transiciones dada responde a la secuencia de señales ambientales
0111000010110...
con las salidas
10000011001000.......
En cada etapa de su funcionamiento, la
salida del glovito es su pronóstico de
cuál será la próxima señal que llegará
procedente del entorno. Para hallar el
número de pronósticos correctos, se
desplaza la secuencia de salida un símbolo hacia la derecha, y se la compara.
bit a bit, con la secuencia de entrada,
Contemos el número de símbolos concordantes. En este caso, el glovito tan
sólo predijo correctamente seis de los
doce símbolos que le fueron llegando,
puntuación no superior a lo que sería
de esperar pronosticando al puro azar.
Es fácil pedir demasiado a los autómatas finitos. En efecto, no hay derecho a exigirle a un glovito que sea capaz de pronosticar correctamente las
señales de medios ambientales. Intentemos reflexionar por un momento sobre esta cuestión. ¿Por qué habrá de
constar toda secuencia correctamente
predicha de una ristra fija de símbolos,
interminablemente repetida? Por
ejemplo, el glovito de tres estados que
antes fracasó en la prueba de predicción que le propusimos, triunfa brillantemente en la siguiente secuencia ambiental:
0100110100110100l1 . . .
Pero aquí la sucesión de valores ambientales desfila al compás de un sencillo redoble, a saher, 010011.
Existen varias docenas de glovitos
triestado, pero tan solo unos pocos son
capaces de predecir correctamenie esta
secuencia. Los glovitos de más de tres
estados con capacidad de predicción
perfecta para una sucesión ambiental
determinada son raros, y escasean
tanto más cuanto mayor es el número
de estados. La predictibilidad depende
fuertemenle del período de la sucesión.
Si la serie fundamental de símbolos es
sufícientemente larga, ningún glovito
número prefijado, n, de estados
conseguirá jamás llegar a pronosticarla
perfectamente. Existe, evidentemente,
una relación entre el número de estados que puede adoptar un glovito y la
máxima longitud del período que es capaz de pronosticar perfectamente. Seguramente los lectores gusten de descubrir por sí mismos tal relación. ¿Cuál
es la máxima longitud de período que
puede pronosticar un glovito de n estados?
Los glovitos son algo más que autómatas finitos que se esfuerzan por predecir su entorno, pues tienen un cromosoma. Por algún procedimiento (que veremos más adelante) los glovitos engendran periódicamente nuevos glovitos. Al examinar el cromosoma del glovito y ponerlo en relación con el automata finito correspondiente, vemos de
qué modo los genes hereditarios determinan el comportamienlo de la progenie. Comencemos con la tabla de transiciones de estados y vayamos separando. una por una, las filas. de arriba
abajo. Unamos las filas, pegando la
cola de cada una con la cabeza de la
siguicnte y, finalmente, el comienzo con
el fin de la tira así obtenida- El resultado será un cromosoma circular.
Antes de llevar a cabo esta última
operación de empalme, el cromosoma
de nuestro ejemplar triestado se nos
presenta como una ristra de 12 genes:
1 B 1 C 0 C 0 B 1 A 0 A
En puridad, los símbolos de esta serie
son alelos. Un alelo es una forma es~
pecífica de gen, que se asienta en un
locus determinado. Los genes pueden
por tanto, especificarse tanto por su
nombre como por su emplazamiento, o
locus. Así pues, el séptimo símbolo,
contando desde la izquierda, controla
el símbolo de salida de un glovito
cuando éste se encuentra en estado B
y se recibe un 1 procedente del en-
torno. Aquí, el locus es 7.
Hace poco preparé en mi ordenador
personal una sopa primordial, con 10
glovitos tetraestado. No habían transcurrido 1000 de las unidades de tiempo.
que llamo cronones, cuado ninguno de
los glovitos originales permanecía con
vida. Todos habían sido remplazados
por otros de mayor habilidad de predicción. La pantalla de mi ordenador
iba mostrando las puntuaciones máxima y minina alcanzadas por la poblacíón existente en ese momento. La
puntuación mínínima fluctuaba fuertemente; la máxima, en cambio, fue trepando poco a poco (véase la figura).
Justanente cuando comenzaba yo a desesperar de que pudiera evolucionar un
predictor perfecto apareció uno súbitamente y, a partir de ahi, la puntuacion máxima quedó estancada en 100.
Todo lo cual suscita la cuestión de
cómo evolucionan exactamente los glovitos en mi caldo computarizado. Periódicamente, un rayo cósmico atraviesa la sopa e impacta al azar en un
cromosoma, en un lugar igualmenle
aleatorio. El resultado de ello es que
un gen específico pasa de un alelo a
otro. Por ejeraplo. en el siguiente cromosoma, que pertenece a un glovito de
cuatro estados, el gen sustituido en el locus 3 controla el símbolo de salida correspondientc a la transición desde el
estado A, cuando a la criatura le llega
un 1.
0 D 1 C 0 D 0 B 1 A 0 C 1 B 1 A
Un rayo cósmico impacta en este gen,
y modifica ligeramente su cromosoma:
0 D 0 C 0 D 0 B 1 A 0 C 1 B 1 A
La otra fuente de variación del
acervo génico de los glovitos es el
apareamiento. Durante la estación de
procreación. el glovito de máxima puntuación intercambia genes con otro elegido al azar. La descendencia porta un
cromosoma compuesto. Parte de él
proviene del progenitor superior, la
otra. del ganador en la lotería de apareamiento. La composición se asemeja al fenómeno de entrecruzamiento que
se da en los cromosornas reales. En los
cromosomas de los glovitos. el entrecruzamiento puede ilustrarse combinando el primero de los cromosomas antes mencionados (sin alteración) con
otro
1 A 1 B 0 D 1 A 0 C 1 D 1 B
^ ^
| |
Las flechas indican los puntos de entrecruzamiento, elegidos de forma estocástica. El eromosoma descendiente es
idéntico al del segundo progenitor
hasta llegar al primer punto de cruzamiento. Entre dicho punto y el segundo
es idéntico a la correspondiente porción del cromosoma del primero. Tras
el segundo punto es nuevamente idéntico al cromosoma del segundo progenitor (véase la figura 3)
1A1CODOB0C1D1B0C
Antes de decidirine a redactar y poner a prueba el programa primordial
era yo un tanto escéptico acerca del va
lor del apareamiento por cruce. Descubrí con sorpresa, sin embargo, que si
el primer progenitor es razonablemente acertado en sus pronósticos, la
descendencia tiende a serlo también.
Los lectores pueden juzgar por si
mismos preparando un programa que
llamaremos AUTOSOPA.
Al listarlo el
programa no excede demasiado de una
página.
0111000010110...
con las salidas
10000011001000.......
En cada etapa de su funcionamiento, la
salida del glovito es su pronóstico de
cuál será la próxima señal que llegará
procedente del entorno. Para hallar el
número de pronósticos correctos, se
desplaza la secuencia de salida un símbolo hacia la derecha, y se la compara.
bit a bit, con la secuencia de entrada,
Contemos el número de símbolos concordantes. En este caso, el glovito tan
sólo predijo correctamente seis de los
doce símbolos que le fueron llegando,
puntuación no superior a lo que sería
de esperar pronosticando al puro azar.
Es fácil pedir demasiado a los autómatas finitos. En efecto, no hay derecho a exigirle a un glovito que sea capaz de pronosticar correctamente las
señales de medios ambientales. Intentemos reflexionar por un momento sobre esta cuestión. ¿Por qué habrá de
constar toda secuencia correctamente
predicha de una ristra fija de símbolos,
interminablemente repetida? Por
ejemplo, el glovito de tres estados que
antes fracasó en la prueba de predicción que le propusimos, triunfa brillantemente en la siguiente secuencia ambiental:
0100110100110100l1 . . .
Pero aquí la sucesión de valores ambientales desfila al compás de un sencillo redoble, a saher, 010011.
Existen varias docenas de glovitos
triestado, pero tan solo unos pocos son
capaces de predecir correctamenie esta
secuencia. Los glovitos de más de tres
estados con capacidad de predicción
perfecta para una sucesión ambiental
determinada son raros, y escasean
tanto más cuanto mayor es el número
de estados. La predictibilidad depende
fuertemenle del período de la sucesión.
Si la serie fundamental de símbolos es
sufícientemente larga, ningún glovito
número prefijado, n, de estados
conseguirá jamás llegar a pronosticarla
perfectamente. Existe, evidentemente,
una relación entre el número de estados que puede adoptar un glovito y la
máxima longitud del período que es capaz de pronosticar perfectamente. Seguramente los lectores gusten de descubrir por sí mismos tal relación. ¿Cuál
es la máxima longitud de período que
puede pronosticar un glovito de n estados?
Los glovitos son algo más que autómatas finitos que se esfuerzan por predecir su entorno, pues tienen un cromosoma. Por algún procedimiento (que veremos más adelante) los glovitos engendran periódicamente nuevos glovitos. Al examinar el cromosoma del glovito y ponerlo en relación con el automata finito correspondiente, vemos de
qué modo los genes hereditarios determinan el comportamienlo de la progenie. Comencemos con la tabla de transiciones de estados y vayamos separando. una por una, las filas. de arriba
abajo. Unamos las filas, pegando la
cola de cada una con la cabeza de la
siguicnte y, finalmente, el comienzo con
el fin de la tira así obtenida- El resultado será un cromosoma circular.
Antes de llevar a cabo esta última
operación de empalme, el cromosoma
de nuestro ejemplar triestado se nos
presenta como una ristra de 12 genes:
1 B 1 C 0 C 0 B 1 A 0 A
En puridad, los símbolos de esta serie
son alelos. Un alelo es una forma es~
pecífica de gen, que se asienta en un
locus determinado. Los genes pueden
por tanto, especificarse tanto por su
nombre como por su emplazamiento, o
locus. Así pues, el séptimo símbolo,
contando desde la izquierda, controla
el símbolo de salida de un glovito
cuando éste se encuentra en estado B
y se recibe un 1 procedente del en-
torno. Aquí, el locus es 7.
Hace poco preparé en mi ordenador
personal una sopa primordial, con 10
glovitos tetraestado. No habían transcurrido 1000 de las unidades de tiempo.
que llamo cronones, cuado ninguno de
los glovitos originales permanecía con
vida. Todos habían sido remplazados
por otros de mayor habilidad de predicción. La pantalla de mi ordenador
iba mostrando las puntuaciones máxima y minina alcanzadas por la poblacíón existente en ese momento. La
puntuación mínínima fluctuaba fuertemente; la máxima, en cambio, fue trepando poco a poco (véase la figura).
Justanente cuando comenzaba yo a desesperar de que pudiera evolucionar un
predictor perfecto apareció uno súbitamente y, a partir de ahi, la puntuacion máxima quedó estancada en 100.
Todo lo cual suscita la cuestión de
cómo evolucionan exactamente los glovitos en mi caldo computarizado. Periódicamente, un rayo cósmico atraviesa la sopa e impacta al azar en un
cromosoma, en un lugar igualmenle
aleatorio. El resultado de ello es que
un gen específico pasa de un alelo a
otro. Por ejeraplo. en el siguiente cromosoma, que pertenece a un glovito de
cuatro estados, el gen sustituido en el locus 3 controla el símbolo de salida correspondientc a la transición desde el
estado A, cuando a la criatura le llega
un 1.
0 D 1 C 0 D 0 B 1 A 0 C 1 B 1 A
Un rayo cósmico impacta en este gen,
y modifica ligeramente su cromosoma:
0 D 0 C 0 D 0 B 1 A 0 C 1 B 1 A
La otra fuente de variación del
acervo génico de los glovitos es el
apareamiento. Durante la estación de
procreación. el glovito de máxima puntuación intercambia genes con otro elegido al azar. La descendencia porta un
cromosoma compuesto. Parte de él
proviene del progenitor superior, la
otra. del ganador en la lotería de apareamiento. La composición se asemeja al fenómeno de entrecruzamiento que
se da en los cromosornas reales. En los
cromosomas de los glovitos. el entrecruzamiento puede ilustrarse combinando el primero de los cromosomas antes mencionados (sin alteración) con
otro
1 A 1 B 0 D 1 A 0 C 1 D 1 B
^ ^
| |
Las flechas indican los puntos de entrecruzamiento, elegidos de forma estocástica. El eromosoma descendiente es
idéntico al del segundo progenitor
hasta llegar al primer punto de cruzamiento. Entre dicho punto y el segundo
es idéntico a la correspondiente porción del cromosoma del primero. Tras
el segundo punto es nuevamente idéntico al cromosoma del segundo progenitor (véase la figura 3)
1A1CODOB0C1D1B0C
Antes de decidirine a redactar y poner a prueba el programa primordial
era yo un tanto escéptico acerca del va
lor del apareamiento por cruce. Descubrí con sorpresa, sin embargo, que si
el primer progenitor es razonablemente acertado en sus pronósticos, la
descendencia tiende a serlo también.
Los lectores pueden juzgar por si
mismos preparando un programa que
llamaremos AUTOSOPA.
Al listarlo el
programa no excede demasiado de una
página.
10000011001000.......
En cada etapa de su funcionamiento, la
salida del glovito es su pronóstico de
cuál será la próxima señal que llegará
procedente del entorno. Para hallar el
número de pronósticos correctos, se
desplaza la secuencia de salida un símbolo hacia la derecha, y se la compara.
bit a bit, con la secuencia de entrada,
Contemos el número de símbolos concordantes. En este caso, el glovito tan
sólo predijo correctamente seis de los
doce símbolos que le fueron llegando,
puntuación no superior a lo que sería
de esperar pronosticando al puro azar.
Es fácil pedir demasiado a los autómatas finitos. En efecto, no hay derecho a exigirle a un glovito que sea capaz de pronosticar correctamente las
señales de medios ambientales. Intentemos reflexionar por un momento sobre esta cuestión. ¿Por qué habrá de
constar toda secuencia correctamente
predicha de una ristra fija de símbolos,
interminablemente repetida? Por
ejemplo, el glovito de tres estados que
antes fracasó en la prueba de predicción que le propusimos, triunfa brillantemente en la siguiente secuencia ambiental:
0100110100110100l1 . . .
Pero aquí la sucesión de valores ambientales desfila al compás de un sencillo redoble, a saher, 010011.
Existen varias docenas de glovitos
triestado, pero tan solo unos pocos son
capaces de predecir correctamenie esta
secuencia. Los glovitos de más de tres
estados con capacidad de predicción
perfecta para una sucesión ambiental
determinada son raros, y escasean
tanto más cuanto mayor es el número
de estados. La predictibilidad depende
fuertemenle del período de la sucesión.
Si la serie fundamental de símbolos es
sufícientemente larga, ningún glovito
número prefijado, n, de estados
conseguirá jamás llegar a pronosticarla
perfectamente. Existe, evidentemente,
una relación entre el número de estados que puede adoptar un glovito y la
máxima longitud del período que es capaz de pronosticar perfectamente. Seguramente los lectores gusten de descubrir por sí mismos tal relación. ¿Cuál
es la máxima longitud de período que
puede pronosticar un glovito de n estados?
Los glovitos son algo más que autómatas finitos que se esfuerzan por predecir su entorno, pues tienen un cromosoma. Por algún procedimiento (que veremos más adelante) los glovitos engendran periódicamente nuevos glovitos. Al examinar el cromosoma del glovito y ponerlo en relación con el automata finito correspondiente, vemos de
qué modo los genes hereditarios determinan el comportamienlo de la progenie. Comencemos con la tabla de transiciones de estados y vayamos separando. una por una, las filas. de arriba
abajo. Unamos las filas, pegando la
cola de cada una con la cabeza de la
siguicnte y, finalmente, el comienzo con
el fin de la tira así obtenida- El resultado será un cromosoma circular.
Antes de llevar a cabo esta última
operación de empalme, el cromosoma
de nuestro ejemplar triestado se nos
presenta como una ristra de 12 genes:
1 B 1 C 0 C 0 B 1 A 0 A
En puridad, los símbolos de esta serie
son alelos. Un alelo es una forma es~
pecífica de gen, que se asienta en un
locus determinado. Los genes pueden
por tanto, especificarse tanto por su
nombre como por su emplazamiento, o
locus. Así pues, el séptimo símbolo,
contando desde la izquierda, controla
el símbolo de salida de un glovito
cuando éste se encuentra en estado B
y se recibe un 1 procedente del en-
torno. Aquí, el locus es 7.
Hace poco preparé en mi ordenador
personal una sopa primordial, con 10
glovitos tetraestado. No habían transcurrido 1000 de las unidades de tiempo.
que llamo cronones, cuado ninguno de
los glovitos originales permanecía con
vida. Todos habían sido remplazados
por otros de mayor habilidad de predicción. La pantalla de mi ordenador
iba mostrando las puntuaciones máxima y minina alcanzadas por la poblacíón existente en ese momento. La
puntuación mínínima fluctuaba fuertemente; la máxima, en cambio, fue trepando poco a poco (véase la figura).
Justanente cuando comenzaba yo a desesperar de que pudiera evolucionar un
predictor perfecto apareció uno súbitamente y, a partir de ahi, la puntuacion máxima quedó estancada en 100.
Todo lo cual suscita la cuestión de
cómo evolucionan exactamente los glovitos en mi caldo computarizado. Periódicamente, un rayo cósmico atraviesa la sopa e impacta al azar en un
cromosoma, en un lugar igualmenle
aleatorio. El resultado de ello es que
un gen específico pasa de un alelo a
otro. Por ejeraplo. en el siguiente cromosoma, que pertenece a un glovito de
cuatro estados, el gen sustituido en el locus 3 controla el símbolo de salida correspondientc a la transición desde el
estado A, cuando a la criatura le llega
un 1.
0 D 1 C 0 D 0 B 1 A 0 C 1 B 1 A
Un rayo cósmico impacta en este gen,
y modifica ligeramente su cromosoma:
0 D 0 C 0 D 0 B 1 A 0 C 1 B 1 A
La otra fuente de variación del
acervo génico de los glovitos es el
apareamiento. Durante la estación de
procreación. el glovito de máxima puntuación intercambia genes con otro elegido al azar. La descendencia porta un
cromosoma compuesto. Parte de él
proviene del progenitor superior, la
otra. del ganador en la lotería de apareamiento. La composición se asemeja al fenómeno de entrecruzamiento que
se da en los cromosornas reales. En los
cromosomas de los glovitos. el entrecruzamiento puede ilustrarse combinando el primero de los cromosomas antes mencionados (sin alteración) con
otro
1 A 1 B 0 D 1 A 0 C 1 D 1 B
^ ^
| |
Las flechas indican los puntos de entrecruzamiento, elegidos de forma estocástica. El eromosoma descendiente es
idéntico al del segundo progenitor
hasta llegar al primer punto de cruzamiento. Entre dicho punto y el segundo
es idéntico a la correspondiente porción del cromosoma del primero. Tras
el segundo punto es nuevamente idéntico al cromosoma del segundo progenitor (véase la figura 3)
1A1CODOB0C1D1B0C
Antes de decidirine a redactar y poner a prueba el programa primordial
era yo un tanto escéptico acerca del va
lor del apareamiento por cruce. Descubrí con sorpresa, sin embargo, que si
el primer progenitor es razonablemente acertado en sus pronósticos, la
descendencia tiende a serlo también.
Los lectores pueden juzgar por si
mismos preparando un programa que
llamaremos AUTOSOPA.
Al listarlo el
programa no excede demasiado de una
página.
Contemos el número de símbolos concordantes. En este caso, el glovito tan
sólo predijo correctamente seis de los
doce símbolos que le fueron llegando,
puntuación no superior a lo que sería
de esperar pronosticando al puro azar.
Es fácil pedir demasiado a los autómatas finitos. En efecto, no hay derecho a exigirle a un glovito que sea capaz de pronosticar correctamente las
señales de medios ambientales. Intentemos reflexionar por un momento sobre esta cuestión. ¿Por qué habrá de
constar toda secuencia correctamente
predicha de una ristra fija de símbolos,
interminablemente repetida? Por
ejemplo, el glovito de tres estados que
antes fracasó en la prueba de predicción que le propusimos, triunfa brillantemente en la siguiente secuencia ambiental:
0100110100110100l1 . . .
Pero aquí la sucesión de valores ambientales desfila al compás de un sencillo redoble, a saher, 010011.
Existen varias docenas de glovitos
triestado, pero tan solo unos pocos son
capaces de predecir correctamenie esta
secuencia. Los glovitos de más de tres
estados con capacidad de predicción
perfecta para una sucesión ambiental
determinada son raros, y escasean
tanto más cuanto mayor es el número
de estados. La predictibilidad depende
fuertemenle del período de la sucesión.
Si la serie fundamental de símbolos es
sufícientemente larga, ningún glovito
número prefijado, n, de estados
conseguirá jamás llegar a pronosticarla
perfectamente. Existe, evidentemente,
una relación entre el número de estados que puede adoptar un glovito y la
máxima longitud del período que es capaz de pronosticar perfectamente. Seguramente los lectores gusten de descubrir por sí mismos tal relación. ¿Cuál
es la máxima longitud de período que
puede pronosticar un glovito de n estados?
Los glovitos son algo más que autómatas finitos que se esfuerzan por predecir su entorno, pues tienen un cromosoma. Por algún procedimiento (que veremos más adelante) los glovitos engendran periódicamente nuevos glovitos. Al examinar el cromosoma del glovito y ponerlo en relación con el automata finito correspondiente, vemos de
qué modo los genes hereditarios determinan el comportamienlo de la progenie. Comencemos con la tabla de transiciones de estados y vayamos separando. una por una, las filas. de arriba
abajo. Unamos las filas, pegando la
cola de cada una con la cabeza de la
siguicnte y, finalmente, el comienzo con
el fin de la tira así obtenida- El resultado será un cromosoma circular.
Antes de llevar a cabo esta última
operación de empalme, el cromosoma
de nuestro ejemplar triestado se nos
presenta como una ristra de 12 genes:
1 B 1 C 0 C 0 B 1 A 0 A
En puridad, los símbolos de esta serie
son alelos. Un alelo es una forma es~
pecífica de gen, que se asienta en un
locus determinado. Los genes pueden
por tanto, especificarse tanto por su
nombre como por su emplazamiento, o
locus. Así pues, el séptimo símbolo,
contando desde la izquierda, controla
el símbolo de salida de un glovito
cuando éste se encuentra en estado B
y se recibe un 1 procedente del en-
torno. Aquí, el locus es 7.
Hace poco preparé en mi ordenador
personal una sopa primordial, con 10
glovitos tetraestado. No habían transcurrido 1000 de las unidades de tiempo.
que llamo cronones, cuado ninguno de
los glovitos originales permanecía con
vida. Todos habían sido remplazados
por otros de mayor habilidad de predicción. La pantalla de mi ordenador
iba mostrando las puntuaciones máxima y minina alcanzadas por la poblacíón existente en ese momento. La
puntuación mínínima fluctuaba fuertemente; la máxima, en cambio, fue trepando poco a poco (véase la figura).
Justanente cuando comenzaba yo a desesperar de que pudiera evolucionar un
predictor perfecto apareció uno súbitamente y, a partir de ahi, la puntuacion máxima quedó estancada en 100.
Todo lo cual suscita la cuestión de
cómo evolucionan exactamente los glovitos en mi caldo computarizado. Periódicamente, un rayo cósmico atraviesa la sopa e impacta al azar en un
cromosoma, en un lugar igualmenle
aleatorio. El resultado de ello es que
un gen específico pasa de un alelo a
otro. Por ejeraplo. en el siguiente cromosoma, que pertenece a un glovito de
cuatro estados, el gen sustituido en el locus 3 controla el símbolo de salida correspondientc a la transición desde el
estado A, cuando a la criatura le llega
un 1.
0 D 1 C 0 D 0 B 1 A 0 C 1 B 1 A
Un rayo cósmico impacta en este gen,
y modifica ligeramente su cromosoma:
0 D 0 C 0 D 0 B 1 A 0 C 1 B 1 A
La otra fuente de variación del
acervo génico de los glovitos es el
apareamiento. Durante la estación de
procreación. el glovito de máxima puntuación intercambia genes con otro elegido al azar. La descendencia porta un
cromosoma compuesto. Parte de él
proviene del progenitor superior, la
otra. del ganador en la lotería de apareamiento. La composición se asemeja al fenómeno de entrecruzamiento que
se da en los cromosornas reales. En los
cromosomas de los glovitos. el entrecruzamiento puede ilustrarse combinando el primero de los cromosomas antes mencionados (sin alteración) con
otro
1 A 1 B 0 D 1 A 0 C 1 D 1 B
^ ^
| |
Las flechas indican los puntos de entrecruzamiento, elegidos de forma estocástica. El eromosoma descendiente es
idéntico al del segundo progenitor
hasta llegar al primer punto de cruzamiento. Entre dicho punto y el segundo
es idéntico a la correspondiente porción del cromosoma del primero. Tras
el segundo punto es nuevamente idéntico al cromosoma del segundo progenitor (véase la figura 3)
1A1CODOB0C1D1B0C
Antes de decidirine a redactar y poner a prueba el programa primordial
era yo un tanto escéptico acerca del va
lor del apareamiento por cruce. Descubrí con sorpresa, sin embargo, que si
el primer progenitor es razonablemente acertado en sus pronósticos, la
descendencia tiende a serlo también.
Los lectores pueden juzgar por si
mismos preparando un programa que
llamaremos AUTOSOPA.
Al listarlo el
programa no excede demasiado de una
página.
0100110100110100l1 . . .
Pero aquí la sucesión de valores ambientales desfila al compás de un sencillo redoble, a saher, 010011.
Existen varias docenas de glovitos
triestado, pero tan solo unos pocos son
capaces de predecir correctamenie esta
secuencia. Los glovitos de más de tres
estados con capacidad de predicción
perfecta para una sucesión ambiental
determinada son raros, y escasean
tanto más cuanto mayor es el número
de estados. La predictibilidad depende
fuertemenle del período de la sucesión.
Si la serie fundamental de símbolos es
sufícientemente larga, ningún glovito
número prefijado, n, de estados
conseguirá jamás llegar a pronosticarla
perfectamente. Existe, evidentemente,
una relación entre el número de estados que puede adoptar un glovito y la
máxima longitud del período que es capaz de pronosticar perfectamente. Seguramente los lectores gusten de descubrir por sí mismos tal relación. ¿Cuál
es la máxima longitud de período que
puede pronosticar un glovito de n estados?
Los glovitos son algo más que autómatas finitos que se esfuerzan por predecir su entorno, pues tienen un cromosoma. Por algún procedimiento (que veremos más adelante) los glovitos engendran periódicamente nuevos glovitos. Al examinar el cromosoma del glovito y ponerlo en relación con el automata finito correspondiente, vemos de
qué modo los genes hereditarios determinan el comportamienlo de la progenie. Comencemos con la tabla de transiciones de estados y vayamos separando. una por una, las filas. de arriba
abajo. Unamos las filas, pegando la
cola de cada una con la cabeza de la
siguicnte y, finalmente, el comienzo con
el fin de la tira así obtenida- El resultado será un cromosoma circular.
Antes de llevar a cabo esta última
operación de empalme, el cromosoma
de nuestro ejemplar triestado se nos
presenta como una ristra de 12 genes:
1 B 1 C 0 C 0 B 1 A 0 A
En puridad, los símbolos de esta serie
son alelos. Un alelo es una forma es~
pecífica de gen, que se asienta en un
locus determinado. Los genes pueden
por tanto, especificarse tanto por su
nombre como por su emplazamiento, o
locus. Así pues, el séptimo símbolo,
contando desde la izquierda, controla
el símbolo de salida de un glovito
cuando éste se encuentra en estado B
y se recibe un 1 procedente del en-
torno. Aquí, el locus es 7.
Hace poco preparé en mi ordenador
personal una sopa primordial, con 10
glovitos tetraestado. No habían transcurrido 1000 de las unidades de tiempo.
que llamo cronones, cuado ninguno de
los glovitos originales permanecía con
vida. Todos habían sido remplazados
por otros de mayor habilidad de predicción. La pantalla de mi ordenador
iba mostrando las puntuaciones máxima y minina alcanzadas por la poblacíón existente en ese momento. La
puntuación mínínima fluctuaba fuertemente; la máxima, en cambio, fue trepando poco a poco (véase la figura).
Justanente cuando comenzaba yo a desesperar de que pudiera evolucionar un
predictor perfecto apareció uno súbitamente y, a partir de ahi, la puntuacion máxima quedó estancada en 100.
Todo lo cual suscita la cuestión de
cómo evolucionan exactamente los glovitos en mi caldo computarizado. Periódicamente, un rayo cósmico atraviesa la sopa e impacta al azar en un
cromosoma, en un lugar igualmenle
aleatorio. El resultado de ello es que
un gen específico pasa de un alelo a
otro. Por ejeraplo. en el siguiente cromosoma, que pertenece a un glovito de
cuatro estados, el gen sustituido en el locus 3 controla el símbolo de salida correspondientc a la transición desde el
estado A, cuando a la criatura le llega
un 1.
0 D 1 C 0 D 0 B 1 A 0 C 1 B 1 A
Un rayo cósmico impacta en este gen,
y modifica ligeramente su cromosoma:
0 D 0 C 0 D 0 B 1 A 0 C 1 B 1 A
La otra fuente de variación del
acervo génico de los glovitos es el
apareamiento. Durante la estación de
procreación. el glovito de máxima puntuación intercambia genes con otro elegido al azar. La descendencia porta un
cromosoma compuesto. Parte de él
proviene del progenitor superior, la
otra. del ganador en la lotería de apareamiento. La composición se asemeja al fenómeno de entrecruzamiento que
se da en los cromosornas reales. En los
cromosomas de los glovitos. el entrecruzamiento puede ilustrarse combinando el primero de los cromosomas antes mencionados (sin alteración) con
otro
1 A 1 B 0 D 1 A 0 C 1 D 1 B
^ ^
| |
Las flechas indican los puntos de entrecruzamiento, elegidos de forma estocástica. El eromosoma descendiente es
idéntico al del segundo progenitor
hasta llegar al primer punto de cruzamiento. Entre dicho punto y el segundo
es idéntico a la correspondiente porción del cromosoma del primero. Tras
el segundo punto es nuevamente idéntico al cromosoma del segundo progenitor (véase la figura 3)
1A1CODOB0C1D1B0C
Antes de decidirine a redactar y poner a prueba el programa primordial
era yo un tanto escéptico acerca del va
lor del apareamiento por cruce. Descubrí con sorpresa, sin embargo, que si
el primer progenitor es razonablemente acertado en sus pronósticos, la
descendencia tiende a serlo también.
Los lectores pueden juzgar por si
mismos preparando un programa que
llamaremos AUTOSOPA.
Al listarlo el
programa no excede demasiado de una
página.
La predictibilidad depende
fuertemenle del período de la sucesión.
Si la serie fundamental de símbolos es
sufícientemente larga, ningún glovito
número prefijado, n, de estados
conseguirá jamás llegar a pronosticarla
perfectamente. Existe, evidentemente,
una relación entre el número de estados que puede adoptar un glovito y la
máxima longitud del período que es capaz de pronosticar perfectamente. Seguramente los lectores gusten de descubrir por sí mismos tal relación. ¿Cuál
es la máxima longitud de período que
puede pronosticar un glovito de n estados?
Los glovitos son algo más que autómatas finitos que se esfuerzan por predecir su entorno, pues tienen un cromosoma. Por algún procedimiento (que veremos más adelante) los glovitos engendran periódicamente nuevos glovitos. Al examinar el cromosoma del glovito y ponerlo en relación con el automata finito correspondiente, vemos de
qué modo los genes hereditarios determinan el comportamienlo de la progenie. Comencemos con la tabla de transiciones de estados y vayamos separando. una por una, las filas. de arriba
abajo. Unamos las filas, pegando la
cola de cada una con la cabeza de la
siguicnte y, finalmente, el comienzo con
el fin de la tira así obtenida- El resultado será un cromosoma circular.
Antes de llevar a cabo esta última
operación de empalme, el cromosoma
de nuestro ejemplar triestado se nos
presenta como una ristra de 12 genes:
1 B 1 C 0 C 0 B 1 A 0 A
En puridad, los símbolos de esta serie
son alelos. Un alelo es una forma es~
pecífica de gen, que se asienta en un
locus determinado. Los genes pueden
por tanto, especificarse tanto por su
nombre como por su emplazamiento, o
locus. Así pues, el séptimo símbolo,
contando desde la izquierda, controla
el símbolo de salida de un glovito
cuando éste se encuentra en estado B
y se recibe un 1 procedente del en-
torno. Aquí, el locus es 7.
Hace poco preparé en mi ordenador
personal una sopa primordial, con 10
glovitos tetraestado. No habían transcurrido 1000 de las unidades de tiempo.
que llamo cronones, cuado ninguno de
los glovitos originales permanecía con
vida. Todos habían sido remplazados
por otros de mayor habilidad de predicción. La pantalla de mi ordenador
iba mostrando las puntuaciones máxima y minina alcanzadas por la poblacíón existente en ese momento. La
puntuación mínínima fluctuaba fuertemente; la máxima, en cambio, fue trepando poco a poco (véase la figura).
Justanente cuando comenzaba yo a desesperar de que pudiera evolucionar un
predictor perfecto apareció uno súbitamente y, a partir de ahi, la puntuacion máxima quedó estancada en 100.
Todo lo cual suscita la cuestión de
cómo evolucionan exactamente los glovitos en mi caldo computarizado. Periódicamente, un rayo cósmico atraviesa la sopa e impacta al azar en un
cromosoma, en un lugar igualmenle
aleatorio. El resultado de ello es que
un gen específico pasa de un alelo a
otro. Por ejeraplo. en el siguiente cromosoma, que pertenece a un glovito de
cuatro estados, el gen sustituido en el locus 3 controla el símbolo de salida correspondientc a la transición desde el
estado A, cuando a la criatura le llega
un 1.
0 D 1 C 0 D 0 B 1 A 0 C 1 B 1 A
Un rayo cósmico impacta en este gen,
y modifica ligeramente su cromosoma:
0 D 0 C 0 D 0 B 1 A 0 C 1 B 1 A
La otra fuente de variación del
acervo génico de los glovitos es el
apareamiento. Durante la estación de
procreación. el glovito de máxima puntuación intercambia genes con otro elegido al azar. La descendencia porta un
cromosoma compuesto. Parte de él
proviene del progenitor superior, la
otra. del ganador en la lotería de apareamiento. La composición se asemeja al fenómeno de entrecruzamiento que
se da en los cromosornas reales. En los
cromosomas de los glovitos. el entrecruzamiento puede ilustrarse combinando el primero de los cromosomas antes mencionados (sin alteración) con
otro
1 A 1 B 0 D 1 A 0 C 1 D 1 B
^ ^
| |
Las flechas indican los puntos de entrecruzamiento, elegidos de forma estocástica. El eromosoma descendiente es
idéntico al del segundo progenitor
hasta llegar al primer punto de cruzamiento. Entre dicho punto y el segundo
es idéntico a la correspondiente porción del cromosoma del primero. Tras
el segundo punto es nuevamente idéntico al cromosoma del segundo progenitor (véase la figura 3)
1A1CODOB0C1D1B0C
Antes de decidirine a redactar y poner a prueba el programa primordial
era yo un tanto escéptico acerca del va
lor del apareamiento por cruce. Descubrí con sorpresa, sin embargo, que si
el primer progenitor es razonablemente acertado en sus pronósticos, la
descendencia tiende a serlo también.
Los lectores pueden juzgar por si
mismos preparando un programa que
llamaremos AUTOSOPA.
Al listarlo el
programa no excede demasiado de una
página.
Los glovitos son algo más que autómatas finitos que se esfuerzan por predecir su entorno, pues tienen un cromosoma. Por algún procedimiento (que veremos más adelante) los glovitos engendran periódicamente nuevos glovitos. Al examinar el cromosoma del glovito y ponerlo en relación con el automata finito correspondiente, vemos de
qué modo los genes hereditarios determinan el comportamienlo de la progenie. Comencemos con la tabla de transiciones de estados y vayamos separando. una por una, las filas. de arriba
abajo. Unamos las filas, pegando la
cola de cada una con la cabeza de la
siguicnte y, finalmente, el comienzo con
el fin de la tira así obtenida- El resultado será un cromosoma circular.
Antes de llevar a cabo esta última
operación de empalme, el cromosoma
de nuestro ejemplar triestado se nos
presenta como una ristra de 12 genes:
1 B 1 C 0 C 0 B 1 A 0 A
En puridad, los símbolos de esta serie
son alelos. Un alelo es una forma es~
pecífica de gen, que se asienta en un
locus determinado. Los genes pueden
por tanto, especificarse tanto por su
nombre como por su emplazamiento, o
locus. Así pues, el séptimo símbolo,
contando desde la izquierda, controla
el símbolo de salida de un glovito
cuando éste se encuentra en estado B
y se recibe un 1 procedente del en-
torno. Aquí, el locus es 7.
Hace poco preparé en mi ordenador
personal una sopa primordial, con 10
glovitos tetraestado. No habían transcurrido 1000 de las unidades de tiempo.
que llamo cronones, cuado ninguno de
los glovitos originales permanecía con
vida. Todos habían sido remplazados
por otros de mayor habilidad de predicción. La pantalla de mi ordenador
iba mostrando las puntuaciones máxima y minina alcanzadas por la poblacíón existente en ese momento. La
puntuación mínínima fluctuaba fuertemente; la máxima, en cambio, fue trepando poco a poco (véase la figura).
Justanente cuando comenzaba yo a desesperar de que pudiera evolucionar un
predictor perfecto apareció uno súbitamente y, a partir de ahi, la puntuacion máxima quedó estancada en 100.
Todo lo cual suscita la cuestión de
cómo evolucionan exactamente los glovitos en mi caldo computarizado. Periódicamente, un rayo cósmico atraviesa la sopa e impacta al azar en un
cromosoma, en un lugar igualmenle
aleatorio. El resultado de ello es que
un gen específico pasa de un alelo a
otro. Por ejeraplo. en el siguiente cromosoma, que pertenece a un glovito de
cuatro estados, el gen sustituido en el locus 3 controla el símbolo de salida correspondientc a la transición desde el
estado A, cuando a la criatura le llega
un 1.
0 D 1 C 0 D 0 B 1 A 0 C 1 B 1 A
Un rayo cósmico impacta en este gen,
y modifica ligeramente su cromosoma:
0 D 0 C 0 D 0 B 1 A 0 C 1 B 1 A
La otra fuente de variación del
acervo génico de los glovitos es el
apareamiento. Durante la estación de
procreación. el glovito de máxima puntuación intercambia genes con otro elegido al azar. La descendencia porta un
cromosoma compuesto. Parte de él
proviene del progenitor superior, la
otra. del ganador en la lotería de apareamiento. La composición se asemeja al fenómeno de entrecruzamiento que
se da en los cromosornas reales. En los
cromosomas de los glovitos. el entrecruzamiento puede ilustrarse combinando el primero de los cromosomas antes mencionados (sin alteración) con
otro
1 A 1 B 0 D 1 A 0 C 1 D 1 B
^ ^
| |
Las flechas indican los puntos de entrecruzamiento, elegidos de forma estocástica. El eromosoma descendiente es
idéntico al del segundo progenitor
hasta llegar al primer punto de cruzamiento. Entre dicho punto y el segundo
es idéntico a la correspondiente porción del cromosoma del primero. Tras
el segundo punto es nuevamente idéntico al cromosoma del segundo progenitor (véase la figura 3)
1A1CODOB0C1D1B0C
Antes de decidirine a redactar y poner a prueba el programa primordial
era yo un tanto escéptico acerca del va
lor del apareamiento por cruce. Descubrí con sorpresa, sin embargo, que si
el primer progenitor es razonablemente acertado en sus pronósticos, la
descendencia tiende a serlo también.
Los lectores pueden juzgar por si
mismos preparando un programa que
llamaremos AUTOSOPA.
Al listarlo el
programa no excede demasiado de una
página.
El resultado será un cromosoma circular.
Antes de llevar a cabo esta última
operación de empalme, el cromosoma
de nuestro ejemplar triestado se nos
presenta como una ristra de 12 genes:
1 B 1 C 0 C 0 B 1 A 0 A
En puridad, los símbolos de esta serie
son alelos. Un alelo es una forma es~
pecífica de gen, que se asienta en un
locus determinado. Los genes pueden
por tanto, especificarse tanto por su
nombre como por su emplazamiento, o
locus. Así pues, el séptimo símbolo,
contando desde la izquierda, controla
el símbolo de salida de un glovito
cuando éste se encuentra en estado B
y se recibe un 1 procedente del en-
torno. Aquí, el locus es 7.
Hace poco preparé en mi ordenador
personal una sopa primordial, con 10
glovitos tetraestado. No habían transcurrido 1000 de las unidades de tiempo.
que llamo cronones, cuado ninguno de
los glovitos originales permanecía con
vida. Todos habían sido remplazados
por otros de mayor habilidad de predicción. La pantalla de mi ordenador
iba mostrando las puntuaciones máxima y minina alcanzadas por la poblacíón existente en ese momento. La
puntuación mínínima fluctuaba fuertemente; la máxima, en cambio, fue trepando poco a poco (véase la figura).
Justanente cuando comenzaba yo a desesperar de que pudiera evolucionar un
predictor perfecto apareció uno súbitamente y, a partir de ahi, la puntuacion máxima quedó estancada en 100.
Todo lo cual suscita la cuestión de
cómo evolucionan exactamente los glovitos en mi caldo computarizado. Periódicamente, un rayo cósmico atraviesa la sopa e impacta al azar en un
cromosoma, en un lugar igualmenle
aleatorio. El resultado de ello es que
un gen específico pasa de un alelo a
otro. Por ejeraplo. en el siguiente cromosoma, que pertenece a un glovito de
cuatro estados, el gen sustituido en el locus 3 controla el símbolo de salida correspondientc a la transición desde el
estado A, cuando a la criatura le llega
un 1.
0 D 1 C 0 D 0 B 1 A 0 C 1 B 1 A
Un rayo cósmico impacta en este gen,
y modifica ligeramente su cromosoma:
0 D 0 C 0 D 0 B 1 A 0 C 1 B 1 A
La otra fuente de variación del
acervo génico de los glovitos es el
apareamiento. Durante la estación de
procreación. el glovito de máxima puntuación intercambia genes con otro elegido al azar. La descendencia porta un
cromosoma compuesto. Parte de él
proviene del progenitor superior, la
otra. del ganador en la lotería de apareamiento. La composición se asemeja al fenómeno de entrecruzamiento que
se da en los cromosornas reales. En los
cromosomas de los glovitos. el entrecruzamiento puede ilustrarse combinando el primero de los cromosomas antes mencionados (sin alteración) con
otro
1 A 1 B 0 D 1 A 0 C 1 D 1 B
^ ^
| |
Las flechas indican los puntos de entrecruzamiento, elegidos de forma estocástica. El eromosoma descendiente es
idéntico al del segundo progenitor
hasta llegar al primer punto de cruzamiento. Entre dicho punto y el segundo
es idéntico a la correspondiente porción del cromosoma del primero. Tras
el segundo punto es nuevamente idéntico al cromosoma del segundo progenitor (véase la figura 3)
1A1CODOB0C1D1B0C
Antes de decidirine a redactar y poner a prueba el programa primordial
era yo un tanto escéptico acerca del va
lor del apareamiento por cruce. Descubrí con sorpresa, sin embargo, que si
el primer progenitor es razonablemente acertado en sus pronósticos, la
descendencia tiende a serlo también.
Los lectores pueden juzgar por si
mismos preparando un programa que
llamaremos AUTOSOPA.
Al listarlo el
programa no excede demasiado de una
página.
En puridad, los símbolos de esta serie
son alelos. Un alelo es una forma es~
pecífica de gen, que se asienta en un
locus determinado. Los genes pueden
por tanto, especificarse tanto por su
nombre como por su emplazamiento, o
locus. Así pues, el séptimo símbolo,
contando desde la izquierda, controla
el símbolo de salida de un glovito
cuando éste se encuentra en estado B
y se recibe un 1 procedente del en-
torno. Aquí, el locus es 7.
Hace poco preparé en mi ordenador
personal una sopa primordial, con 10
glovitos tetraestado. No habían transcurrido 1000 de las unidades de tiempo.
que llamo cronones, cuado ninguno de
los glovitos originales permanecía con
vida. Todos habían sido remplazados
por otros de mayor habilidad de predicción. La pantalla de mi ordenador
iba mostrando las puntuaciones máxima y minina alcanzadas por la poblacíón existente en ese momento. La
puntuación mínínima fluctuaba fuertemente; la máxima, en cambio, fue trepando poco a poco (véase la figura).
Justanente cuando comenzaba yo a desesperar de que pudiera evolucionar un
predictor perfecto apareció uno súbitamente y, a partir de ahi, la puntuacion máxima quedó estancada en 100.
Todo lo cual suscita la cuestión de
cómo evolucionan exactamente los glovitos en mi caldo computarizado. Periódicamente, un rayo cósmico atraviesa la sopa e impacta al azar en un
cromosoma, en un lugar igualmenle
aleatorio. El resultado de ello es que
un gen específico pasa de un alelo a
otro. Por ejeraplo. en el siguiente cromosoma, que pertenece a un glovito de
cuatro estados, el gen sustituido en el locus 3 controla el símbolo de salida correspondientc a la transición desde el
estado A, cuando a la criatura le llega
un 1.
0 D 1 C 0 D 0 B 1 A 0 C 1 B 1 A
Un rayo cósmico impacta en este gen,
y modifica ligeramente su cromosoma:
0 D 0 C 0 D 0 B 1 A 0 C 1 B 1 A
La otra fuente de variación del
acervo génico de los glovitos es el
apareamiento. Durante la estación de
procreación. el glovito de máxima puntuación intercambia genes con otro elegido al azar. La descendencia porta un
cromosoma compuesto. Parte de él
proviene del progenitor superior, la
otra. del ganador en la lotería de apareamiento. La composición se asemeja al fenómeno de entrecruzamiento que
se da en los cromosornas reales. En los
cromosomas de los glovitos. el entrecruzamiento puede ilustrarse combinando el primero de los cromosomas antes mencionados (sin alteración) con
otro
1 A 1 B 0 D 1 A 0 C 1 D 1 B
^ ^
| |
Las flechas indican los puntos de entrecruzamiento, elegidos de forma estocástica. El eromosoma descendiente es
idéntico al del segundo progenitor
hasta llegar al primer punto de cruzamiento. Entre dicho punto y el segundo
es idéntico a la correspondiente porción del cromosoma del primero. Tras
el segundo punto es nuevamente idéntico al cromosoma del segundo progenitor (véase la figura 3)
1A1CODOB0C1D1B0C
Antes de decidirine a redactar y poner a prueba el programa primordial
era yo un tanto escéptico acerca del va
lor del apareamiento por cruce. Descubrí con sorpresa, sin embargo, que si
el primer progenitor es razonablemente acertado en sus pronósticos, la
descendencia tiende a serlo también.
Los lectores pueden juzgar por si
mismos preparando un programa que
llamaremos AUTOSOPA.
Al listarlo el
programa no excede demasiado de una
página.
Hace poco preparé en mi ordenador
personal una sopa primordial, con 10
glovitos tetraestado. No habían transcurrido 1000 de las unidades de tiempo.
que llamo cronones, cuado ninguno de
los glovitos originales permanecía con
vida. Todos habían sido remplazados
por otros de mayor habilidad de predicción. La pantalla de mi ordenador
iba mostrando las puntuaciones máxima y minina alcanzadas por la poblacíón existente en ese momento. La
puntuación mínínima fluctuaba fuertemente; la máxima, en cambio, fue trepando poco a poco (véase la figura).
Justanente cuando comenzaba yo a desesperar de que pudiera evolucionar un
predictor perfecto apareció uno súbitamente y, a partir de ahi, la puntuacion máxima quedó estancada en 100.
Todo lo cual suscita la cuestión de
cómo evolucionan exactamente los glovitos en mi caldo computarizado. Periódicamente, un rayo cósmico atraviesa la sopa e impacta al azar en un
cromosoma, en un lugar igualmenle
aleatorio. El resultado de ello es que
un gen específico pasa de un alelo a
otro. Por ejeraplo. en el siguiente cromosoma, que pertenece a un glovito de
cuatro estados, el gen sustituido en el locus 3 controla el símbolo de salida correspondientc a la transición desde el
estado A, cuando a la criatura le llega
un 1.
0 D 1 C 0 D 0 B 1 A 0 C 1 B 1 A
Un rayo cósmico impacta en este gen,
y modifica ligeramente su cromosoma:
0 D 0 C 0 D 0 B 1 A 0 C 1 B 1 A
La otra fuente de variación del
acervo génico de los glovitos es el
apareamiento. Durante la estación de
procreación. el glovito de máxima puntuación intercambia genes con otro elegido al azar. La descendencia porta un
cromosoma compuesto. Parte de él
proviene del progenitor superior, la
otra. del ganador en la lotería de apareamiento. La composición se asemeja al fenómeno de entrecruzamiento que
se da en los cromosornas reales. En los
cromosomas de los glovitos. el entrecruzamiento puede ilustrarse combinando el primero de los cromosomas antes mencionados (sin alteración) con
otro
1 A 1 B 0 D 1 A 0 C 1 D 1 B
^ ^
| |
Las flechas indican los puntos de entrecruzamiento, elegidos de forma estocástica. El eromosoma descendiente es
idéntico al del segundo progenitor
hasta llegar al primer punto de cruzamiento. Entre dicho punto y el segundo
es idéntico a la correspondiente porción del cromosoma del primero. Tras
el segundo punto es nuevamente idéntico al cromosoma del segundo progenitor (véase la figura 3)
1A1CODOB0C1D1B0C
Antes de decidirine a redactar y poner a prueba el programa primordial
era yo un tanto escéptico acerca del va
lor del apareamiento por cruce. Descubrí con sorpresa, sin embargo, que si
el primer progenitor es razonablemente acertado en sus pronósticos, la
descendencia tiende a serlo también.
Los lectores pueden juzgar por si
mismos preparando un programa que
llamaremos AUTOSOPA.
Al listarlo el
programa no excede demasiado de una
página.
0 D 1 C 0 D 0 B 1 A 0 C 1 B 1 A
Un rayo cósmico impacta en este gen,
y modifica ligeramente su cromosoma:
0 D 0 C 0 D 0 B 1 A 0 C 1 B 1 A
La otra fuente de variación del
acervo génico de los glovitos es el
apareamiento. Durante la estación de
procreación. el glovito de máxima puntuación intercambia genes con otro elegido al azar. La descendencia porta un
cromosoma compuesto. Parte de él
proviene del progenitor superior, la
otra. del ganador en la lotería de apareamiento. La composición se asemeja al fenómeno de entrecruzamiento que
se da en los cromosornas reales. En los
cromosomas de los glovitos. el entrecruzamiento puede ilustrarse combinando el primero de los cromosomas antes mencionados (sin alteración) con
otro
1 A 1 B 0 D 1 A 0 C 1 D 1 B
^ ^
| |
Las flechas indican los puntos de entrecruzamiento, elegidos de forma estocástica. El eromosoma descendiente es
idéntico al del segundo progenitor
hasta llegar al primer punto de cruzamiento. Entre dicho punto y el segundo
es idéntico a la correspondiente porción del cromosoma del primero. Tras
el segundo punto es nuevamente idéntico al cromosoma del segundo progenitor (véase la figura 3)
1A1CODOB0C1D1B0C
Antes de decidirine a redactar y poner a prueba el programa primordial
era yo un tanto escéptico acerca del va
lor del apareamiento por cruce. Descubrí con sorpresa, sin embargo, que si
el primer progenitor es razonablemente acertado en sus pronósticos, la
descendencia tiende a serlo también.
Los lectores pueden juzgar por si
mismos preparando un programa que
llamaremos AUTOSOPA.
Al listarlo el
programa no excede demasiado de una
página.
0 D 0 C 0 D 0 B 1 A 0 C 1 B 1 A
La otra fuente de variación del
acervo génico de los glovitos es el
apareamiento. Durante la estación de
procreación. el glovito de máxima puntuación intercambia genes con otro elegido al azar. La descendencia porta un
cromosoma compuesto. Parte de él
proviene del progenitor superior, la
otra. del ganador en la lotería de apareamiento. La composición se asemeja al fenómeno de entrecruzamiento que
se da en los cromosornas reales. En los
cromosomas de los glovitos. el entrecruzamiento puede ilustrarse combinando el primero de los cromosomas antes mencionados (sin alteración) con
otro
1 A 1 B 0 D 1 A 0 C 1 D 1 B
^ ^
| |
Las flechas indican los puntos de entrecruzamiento, elegidos de forma estocástica. El eromosoma descendiente es
idéntico al del segundo progenitor
hasta llegar al primer punto de cruzamiento. Entre dicho punto y el segundo
es idéntico a la correspondiente porción del cromosoma del primero. Tras
el segundo punto es nuevamente idéntico al cromosoma del segundo progenitor (véase la figura 3)
1A1CODOB0C1D1B0C
Antes de decidirine a redactar y poner a prueba el programa primordial
era yo un tanto escéptico acerca del va
lor del apareamiento por cruce. Descubrí con sorpresa, sin embargo, que si
el primer progenitor es razonablemente acertado en sus pronósticos, la
descendencia tiende a serlo también.
Los lectores pueden juzgar por si
mismos preparando un programa que
llamaremos AUTOSOPA.
Al listarlo el
programa no excede demasiado de una
página.
1 A 1 B 0 D 1 A 0 C 1 D 1 B
^ ^
| |
Las flechas indican los puntos de entrecruzamiento, elegidos de forma estocástica. El eromosoma descendiente es
idéntico al del segundo progenitor
hasta llegar al primer punto de cruzamiento. Entre dicho punto y el segundo
es idéntico a la correspondiente porción del cromosoma del primero. Tras
el segundo punto es nuevamente idéntico al cromosoma del segundo progenitor (véase la figura 3)
1A1CODOB0C1D1B0C
Antes de decidirine a redactar y poner a prueba el programa primordial
era yo un tanto escéptico acerca del va
lor del apareamiento por cruce. Descubrí con sorpresa, sin embargo, que si
el primer progenitor es razonablemente acertado en sus pronósticos, la
descendencia tiende a serlo también.
Los lectores pueden juzgar por si
mismos preparando un programa que
llamaremos AUTOSOPA.
Al listarlo el
programa no excede demasiado de una
página.
1A1CODOB0C1D1B0C
Antes de decidirine a redactar y poner a prueba el programa primordial
era yo un tanto escéptico acerca del va
lor del apareamiento por cruce. Descubrí con sorpresa, sin embargo, que si
el primer progenitor es razonablemente acertado en sus pronósticos, la
descendencia tiende a serlo también.
Los lectores pueden juzgar por si
mismos preparando un programa que
llamaremos AUTOSOPA.
Al listarlo el
programa no excede demasiado de una
página.
Antes de decidirine a redactar y poner a prueba el programa primordial
era yo un tanto escéptico acerca del va
lor del apareamiento por cruce. Descubrí con sorpresa, sin embargo, que si
el primer progenitor es razonablemente acertado en sus pronósticos, la
descendencia tiende a serlo también.
Los lectores pueden juzgar por si
mismos preparando un programa que
llamaremos AUTOSOPA.