Figure A Significance tests for sex dimorphism
Maxilla trait
tooth bhl
grs raj
CRV I1
0.496 0.999 0.087
WNG I1
0.185 0.393 0.500
SHV I1
0.845 0.483 0.208
SHV I2
0.017 0.039 0.832
SHV C
0.157 0.079 0.902
DSHV I1
0.967 0.184 0.497
DSHV I2
0.341 0.455 0.865
DSHV C
0.198 0.755 0.677
DSHV P3
0.417 0.312 0.673
IG I1
0.311 **
0.540
IG I2
0.572 0.939 0.041
TD I1
0.669 0.044 0.896
TD I2
0.657 0.367 0.310
TD C
0.727 0.394 0.255
CMR C
0.654 0.007 0.485
CDAR C
0.858 0.116 0.155
ME M1
0.907 0.522 0.825
ME M2
0.247 0.613 0.058
ME M3
0.008 0.807 0.445
HYP M1
0.105 0.488 0.010
HYP M2
0.015 0.797 0.627
HYP M3
0.007 0.505 0.413
C5 M1
0.006 0.495 0.713
C5 M2
0.385 0.269 0.150
C5 M3
** 0.821
**
CAR M1
0.113 0.312 0.002
CAR M2
0.442 0.288 0.005
CAR M3
0.001 0.416 0.061
PAR M1
0.159 **
**
PAR M2
0.989 0.951 0.382
PAR M3
0.002 0.241 0.061
PEG I2
0.654 0.400 0.816
PEG M3
** 0.071
0.095
ABS I2
** 0.717
0.527
ABS P4
** 0.585
0.744
ABS M3
** 0.090
0.011
MDN I
0.311 0.509 0.528
sig traits/ total
7/37 3/37
5/37
frequency of significant
sex differences
0.189 0.081 0.135
Figure B Significance tests for sex dimorphism
Mandible trait tooth
bhl grs
raj
SHV C
0.392 0.126 0.721
CDAR C
0.000 0.003 0.006
CNO P3
0.298 0.816 0.289
CNO P4
0.166 0.945 0.363
AFV M1
0.949 0.790 0.000
GRV M1
0.165 0.697 0.232
GRV M2
0.371 0.972 0.003
GRV M3
0.212 0.123 0.335
CNO M1
0.568 0.609 0.178
CNO M2
0.795 0.006 0.211
CNO M3
0.708 0.052 0.296
DWR M1
0.245 0.604 0.205
DWR M2
0.244 0.009 0.630
DWR M3
0.050 **
**
PRSD M1 0.001
0.790 0.317
PRSD M2 0.131
0.827 0.694
PRSD M3 0.075
0.079 0.310
C5 M1
0.370 0.083 0.747
C5 M2
0.659 0.063 0.340
C5 M3
0.633 0.409 0.715
C6 M1
0.817 0.643 0.047
C6 M2
0.322 0.642 0.242
C6 M3
0.379 **
0.140
C7 M1
0.455 0.429 0.835
C7 M2
0.971 0.339 0.037
C7 M3
** 0.773
**
TSOM M3 0.023
0.029 0.001
ABS I1
0.149 0.909
**
ABS P4
0.638 **
**
ABS M3
0.064 0.000 0.000
sig traits/ total
4/30 5/30
7/30
frequency of significant
sex differences
0.133 0.167 0.233
The overall level of asymmetry was not significant, so I used
the traits from the left side to perform
chi-square tests (Figures C and D) for significant differences between
frequencies for all three groups and for
combinations of two groups (Bhil- Garasia, Rajput-Garasia, and Garasia-Bhil).
The chi-square test for
significant differences yields a low p-value when the presence frequencies
for the three groups are
significantly different from one another. The test revealed that although
the three groups appear similar in
many respects, the differences for almost all of the traits were significant
at alpha= 0.05. Because the groups
were significantly different from one another, I went ahead and included
all of the traits in my first analysis.
To test the distance between the three groups, I used the presence
frequencies of the 67 mandibular
and maxillary traits in a Euclidean distance matrix, cluster analysis,
and MMD (Figures E,F, and G
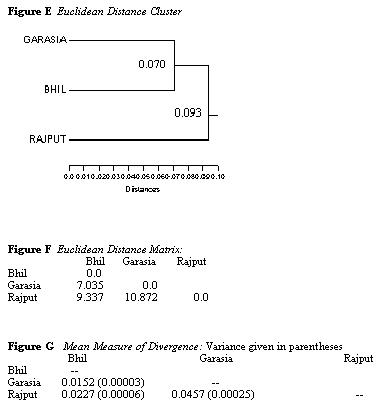
respectively). The Euclidean distance cluster shows that the closest
relationship exists between the Garasias
and the Bhils, confirming the results obtained by Hemphill and Lukacs
(1993). However, the discrete traits
do not assign the Garasia to a position intermediate to the Bhils and
Rajputs. The Bhils and the Rajputs
appear closer and the Garasia are furthest removed from the Rajputs.
This result is confirmed by the Mean
Measure of Divergence test. The MMD was taken from Berry and Berry
(1967) and is calculated with the
formula MMD= (01 - 02)2 - SE. 01= sin -1 (1- 2p), the SE = (1/n1 +
1/n2), the variance for the MMD = 4D2
(SE)).
By calculating the MMD across all of the traits, an assumption
is made that the traits are not highly
correlated between traits. To justify this assumption, I calculated
interclass correlations using Spearman
coefficients for rank ordered data as suggested by Turner and Scott
(1997). Using graded ordinal data, I
measured the correlation of individual teeth within and between tooth
fields for each trait. I also measured
the inter-trait correlation for the Hypocone and Carabelliís trait
(Figure J) because they are usually
considered to be the most highly correlated traits (Turner and Scott,
1997). Almost every trait had
significantly correlated interactions within tooth classes for the
Bhils, Garasias and the Rajputs (Figures H
and I). This fact was considered in the second data reduction which
I will explain later.
Figure C Test for significant differences between groups: Presence Frequencies
and Chi-square P-values
(The insignificant p-values are emboldened, alpha = 0.05)
Maxilla
Raj-Bhl Bhl
Bhl-Grs
Grs Raj-Grs
Raj
3 Groups
trait
tooth
p
%
p
%
p
%
p
CRV
I1
0 72.115
0
75.124
0
68.269
0
WNG
I1
0 0.481
0.025
37.313 0.025
0.962
0.025
SHV
I1
0 86.538
0
82.09
0
78.846
0
SHV
I2
0.002 61.058
0.005
46.766
0.006 50.962
0.006
SHV
C
0.001 56.731
0.001
53.731 0.001
60.096
0.002
DSHV I1
0.009 14.904
0.008
7.96
0.001 11.538
0.009
DSHV I2
0 10.096
0
2.985
0
3.365
0
DSHV C
0.033 19.712
0.031
11.94
0.006 13.462
0.035
DSHV P3
0 1.923
0
4.478
0
6.250
0
IG
I1
0 0.481
0
0
0
0.481
0
IG
I2
0 3.846
0
3.98
0
6.250
0
TD
I1
0.011 46.154
0.011
45.274 0.012
45.673
0.017
TD
I2
0.014 13.942
0.005
9.95
0.009 15.385
0.014
TD
C
0.035 52.885
0.014
41.294 0.047
34.615
0.049
CMR
C
0 2.404
0
3.98
0
4.808
0
CDAR C
0 66.827
0
68.159
0
59.615
0
ME
M1
0 99.038
0
99.502
0
97.596
0
ME
M2
0 89.423
0
87.562
0
86.538
0
ME
M3
0 4.808
0
4.478
0
3.365
0
HYP
M1
0 99.519
0
99.005
0
98.558
0
HYP
M2
0 85.577
0
82.587
0
75.962
0
HYP
M3
0 1.923
0
5.473
0
1.442
0
C5
M1
0.107 26.442
0.08
36.816 0.08
27.885
0.134
C5
M2
0.054 26.923
0.057
12.935 0.003
87.500
0.057
C5
M3
0 0.962
0
0.498
0
0.000
0
CAR
M1
0 56.731
0.003
49.254 0.003
68.750
0.003
CAR
M2
0 3.365
0
2.985
0
2.404
0
CAR
M3
0 0.481
0
0
0
0.000
0
PAR
M1
0 0.962
0
0
0
0.000
0
PAR
M2
0 0.962
0
0
0
0.481
0
PAR
M3
0 0.000
0
0
0
0.000
0
PEG
I2
0.002 7.692
0
8.458 0.002
12.019
0.002
PEG
M3
0 0.000
0
0
0
0.000
0
ABS
I2
0 0.000
0
1.99
0
0.481
0
ABS
P4
0 0.000
0
0
0
0.481
0
ABS
M3
0 0.000
0
0
0
0.000
0
MSD
I
0 0.481
0
1.493
0
0.481
0
Figure D Presence Frequencies and Chi-square P-values: (The insignificant
p-values are emboldened, alpha = 0.05)
Mandible
Raj-Bhl Bhl
Bhl-Grs Grs
Raj-Grs Raj
3 Groups
trait
tooth
p %
p
%
p
%
p
SHV
C
0.027 18.750
0.033 15.347
0.011 12.500
0.036
CDAR
C
0.102 29.808
0.1
30.198
0.101 25.000
0.152
CNO
P3
0 91.346
0
85.149
0
78.125
0
CNO
P4
0.055 28.846
0.054 52.475
0.004 49.479
0.056
AFV
M1
0.008 44.231
0.008 57.426
0
63.542 0.008
GRV
M1
0 72.115
0
71.287
0
70.313
0
GRV
M2
0 81.731
0
79.208
0
78.646
0
GRV
M3
0 5.288
0
2.970
0
3.646
0
CNO
M1
0 91.827
0
95.545
0
97.917
0
CNO
M2
0 91.827
0
91.584
0
91.667
0
CNO
M3
0 6.250
0
2.970
0
4.687
0
DWR
M1
0.089 30.769
0.089 32.673 `
0.083 32.813
0.13
DWR
M2
0 2.885
0
2.475
0
0.000
0
DWR
M3
0 0.000
0
0.000
0
0.000
0
PRSD
M1
0.013 16.346
0.013 3.960
0.001 10.417
0.013
PRSD
M2
0 3.846
0
1.485
0
2.604
0
PRSD
M3
0 0.962
0
0.495
0
0.000
0
C5
M1
0 80.288
0
82.178
0
82.813
0
C5
M2
0.003 12.981
0.004 10.396
0.001 6.771
0.004
C5
M3
0 2.885
0
0.495
0 0.521
0
C6
M1
0 6.731
0
6.436
0 5.729
0
C6
M2
0 1.923
0
0.495
0 1.042
0
C6
M3
0 0.962
0
0.000
0 0.000
0
C7
M1
0 8.173
0
7.426
0 8.854
0
C7
M2
0 0.962
0
0.495
0 0 1.042
0
C7
M3
0 0.000
0
0.495
0 0.000
0
TSOM
M3
0 0.481
0
0.000
0 0.521
0
ABS
I1
0 0.481
0
0.495
0 0.000
0
ABS
P4
0 0.000
0
0.000
0 0.000
0
ABS
M3
0 0.000
0
0.000
0 0.000
0
Figure E Euclidean Distance Cluster

Figure F Euclidean Distance Matrix:
Bhil Garasia
Rajput
Bhil
0.0
Garasia
7.035
0.0
Rajput
9.337 10.872
0.0
Figure G Mean Measure of Divergence: Variance given in parentheses
Bhil
Garasia
Rajput
Bhil
--
Garasia 0.0152 (0.00003)
--
Rajput 0.0227 (0.00006)
0.0457 (0.00025)
--
Figure H Interclass Correlation
Spearman Coefficients between two members of a tooth district for a
single trait
Maxilla
Bhils Garasias Rajputs
Trait (Tooth)
r
r r
SHV (ULI1-ULI2)
0.589 0.459
0.437
SHV (ULI1-ULC)
0.303 0.294
0.304
SHV (ULI2-ULC)
0.311 0.327
0.375
DSHV (ULI1 - ULI2) 0.461
0.323 0.286
DSHV (ULI1 - ULC) 0.074
0.268 0.373
DSHV (ULI1 - ULP3) 0.031
-0.062 0.038
DSHV (ULI2 - ULC) 0.200
0.259 0.175
DSHV (ULI2 - ULP3) 0.060
-0.035 0.074
DSHV (ULC - ULP3) 0.118
0.177 0.269
IG (ULI1- ULI2)
** **
0.267
TD (ULI1 - ULI2)
0.218 0.214
0.333
TD (ULI1 - ULC)
0.357 0.361
0.299
TD (ULI2 - ULC)
0.157 0.000
0.323
ME (ULM1 - ULM2) 0.742
** 0.167
ME (ULM1 - ULM3) 0.108
** -0.255
ME (ULM2 - ULM3) 0.326
0.624 0.255
HYP (ULM1 - ULM2) 0.213
0.410 0.214
HYP (ULM1 - ULM3) 0.135
0.491 0.450
HYP (ULM2 - ULM3) 0.719
0.473 -0.031
Cusp 5 (ULM1 - ULM2) -0.216
**
**
Cusp 5 (ULM1 - ULM2) -0.216
**
**
Cusp 5 (ULM1 - ULM2) 0.959
**
**
CAR (ULM1- ULM2) 0.378
**
**
CAR (ULM1- ULM3) 0.379
**
**
CAR (ULM2- ULM3) 0.728
**
**
Figure I Interclass Correlation
Spearman Coefficients between two members of a tooth district for a
single trait
(Correlations not significantly different from zero are emboldened,
alpha=|0.05|)
Mandible Bhils Garasias Rajputs
Trait (Tooth)
r r
r
CNO (LLP3 - LLP4) -0.451
-0.270 0.821
CNO (LLP3 - LLM1) -0.126
** -0.429
CNO (LLP3 - LLM2) -0.413
** **
CNO (LLP3 - LLM3) -0.421
0.424 0.000
CNO (LLP4 - LLM1) 0.527
** -0.458
CNO (LLP4 - LLM2) 0.310
** **
CNO (LLP4 - LLM3) 0.724
-0.135 0.303
CNO (LLM1 - LLM2) -0.123
** **
CNO (LLM1 - LLM3) 0.450
** 0.189
CNO (LLM2 - LLM3) 0.273
** **
PRSD (LLM1 - LLM2) -0.091 0.734
**
PRSD (LLM1 - LLM3) -0.133 0.734
**
PRSD (LLM2 - LLM3) 0.638 1.000
**
Cusp 5 (LLM1 - LLM2) 0.099
** **
Cusp 5 (LLM1 - LLM3) 0.597 0.167
0.366
Cusp 5 (LLM2 - LLM3) 0.067
** **
Cusp 6 (LLM1 - LLM2) -0.091 **
**
Cusp 6 (LLM1 - LLM3) 0.674
** **
Cusp 6 (LLM2 - LLM3) 0.674
** **
Cusp 7 (LLM1 - LLM3) **
1.000 **
Figure J Inter-trait Correlation
Spearman correlation matrix for Hypocone and Carabelliís traits
Hypocone
ULM1 ULM2 ULM3
Carabelliís
Bhil
ULM1 -0.073 0.424
0.703
ULM2 0.050
0.476 0.693
ULM3 0.333
0.482 0.465
Garasia
ULM1 0.138
0.718 0.498
ULM2 **
** **
ULM3 **
** **
Rajput
ULM1 0.000 -1.000
**
ULM2 **
**
**
ULM3 **
**
**
I used a principle components analysis to understand the relationships
between traits and to identify
the components of the variance between groups. For the principle components
analysis, I used the graded
ordinal data for each individual by each trait, for both jaws (Figures
K). The principle components analysis is
primarily used to understand the underlying components of variance
in morphometric tooth studies but
Mizoguchi (1985) used the analysis with discrete traits. Mizoguchiís
components consisted of high loadings
for individual tooth classes and inter-trait correlations. His analysis
suggested a high level of independence
between traits but dependence within tooth fields (Turner and Scott,
1997).
One difference between using this type of analytical procedure
on metric versus non-metric traits,
seen in both Mizoguchi (1985) and this study, is that there are many
components loaded with fewer variables
and explaining less variance each when compared to the usual results
of the analysis on morphometric data
(Turner and Scott, 1997). One difference between Mizoguchi (1985) and
this study is that these traits were
segregated by class rather than by field. Only the first five components
were included here as they had
eigenvalues greater than one. These five components explained 45% of
the variance in the maxilla and 60%
in the mandible.
Figure K Component Loadings from Principle Components Analysis
(varimax rotation)
Maxilla
Components
traits
1 2
3
4
5
PAR_ULM3
0.909 -0.021
0.045 0.002
0.022
CAR_ULM3
0.885 -0.028
0.073 -0.007
-0.050
HYP_ULM3
0.881 0.029
0.030 0.010
0.003
ABS_ULM3
0.844 0.008
0.040 0.019
0.026
PEG_ULM3
0.842 0.012
0.041 0.024
0.030
C_5_ULM3
0.807 0.007
0.032 -0.003
0.004
ME_ULM3
0.805 0.018
0.013 0.003
0.015
IG_ULI1
0.045 0.852
-0.004 0.047
0.018
TD_ULI1
-0.037 0.779
-0.009 0.144
0.014
IG_ULI2
0.034 0.743
-0.005 0.059
0.070
TD_ULI2
-0.013 0.655
-0.052 0.073
0.089
SHV_ULI1
0.022 0.548
0.020 0.255
0.069
ME_ULM2
0.005 0.013
0.865 0.000
0.014
HYP_ULM2
0.075 -0.002
0.829 -0.004
-0.000
CAR_ULM2
0.014 -0.011
0.825 0.062
0.032
PAR_ULM2
0.027 0.008
0.806 0.050
0.055
C_5_ULM2
0.127 -0.043
0.749 0.030
-0.053
CMR_ULC
0.036 0.158
0.013 0.774
0.090
SHV_ULC
0.012 0.251
0.039 0.741
0.037
DSHV_LC
0.009 -0.006
0.053 0.726
0.033
CDAR_ULC
-0.047 -0.107
-0.033 0.652
0.072
TD_ULC
0.035 0.172
0.097 0.605
-0.042
ABS_ULI2
0.013 0.055
-0.016 0.119
0.915
ABS_ULP4
0.017 0.116
0.059 0.068
0.876
PEG_ULI2
0.023 -0.029
0.000 -0.008
0.712
DSHV_LP3
0.041 -0.048
0.066 0.401
0.089
Variance Explained 13.939
8.544 9.170
7.630 6.086
Mandible
Components
traits
1
2
3
4
5
C_6_LLM3
0.970 0.032
-0.004 -0.028
-0.046
C_5_LLM3
0.936 0.014
0.015 -0.033
-0.060
CNO_LLM3
0.930 0.037
0.013 -0.032
-0.044
C_7_LLM3
0.922 0.038
0.007 -0.015
-0.060
GRV_LLM3
0.849 0.038
0.034 -0.038
-0.028
DWR_LLM3
0.821 -0.028
-0.059 0.068
0.103
PRSD_LM3
0.789 0.037
0.023 -0.023
-0.067
C_6_LLM2
0.034 0.943
0.097 0.076
0.044
CNO_LLM2
0.029 0.905
0.155 0.046
0.037
C_5_LLM2
0.052 0.904
0.105 0.027
0.028
C_7_LLM2
0.022 0.856
0.106 0.131
-0.018
PRSD_LM2
0.055 0.779
0.149 0.112
0.032
GRV_LLM2
-0.029 0.638
0.034 0.015
0.178
CNO_LLM1
-0.002 0.122
0.894 0.047
0.104
C_6_LLM1
0.036 0.112
0.852 0.163
0.147
C_5_LLM1
-0.059 0.088
0.796 -0.092
0.023
C_7_LLM1
0.005 0.100
0.734 0.228
0.103
PRSD_LM1
0.054 0.186
0.622 0.207
0.111
ABS_LLI1
-0.032 0.189
0.251 0.906
0.063
ABS_LLP4
-0.033 0.189
0.252 0.906
0.066
DWR_LLM1
-0.062 0.047
0.188 0.011
0.852
DWR_LLM2
-0.011 0.488
-0.095 0.034
0.696
AFV_LLM1
-0.025 0.041
0.169 0.026
0.592
TSOM_LM3
0.465 0.020
-0.055 0.040
0.006
Variance Explained 19.698
15.596 11.586
6.665 6.391
After analyzing the whole body of data collected, I attempted
to reduce the data and simplify the
analysis. I originally decided to look at the results using the key
teeth for each trait. However, this method
neglected both the results of the chi-square statistic of relatedness
and the frequency of trait expression. The
results of that analysis are included as well as the second data reduction
which I attempted using two
criteria: a significant p-value from the chi-square test as well as
a trait frequency of greater than or equal to
30% in at least one of the three groups.
The following are the statistical test results for the two data
reductions. The first reduction was
based solely on looking at the so called ďkey teethĒ for each trait,
the tooth where the greatest level of
expression would be expected given Dahlbergís morphogenic field idea
(Turner and Scott, 1997). I then
reduced the data a second time using a different set of criteria because
the results of the original reduction
contradicted the results from using all of the traits combined. I felt
that it might be more accurate reduce the
data using two criteria: a significant p-value in the chi-square test
for significant differences as well as a trait
presence frequency of 30 % or greater for at least one population.
The results of those tests follow.
Figure L Trait list for trait reduction #1 (key teeth)
mandible
SHV-LIC CDAR-LLC CNO-LLP3 AFV-LLM1 GRV-LLM1 CNO-LLM1
DWR-LLM1 PRSD-LM1 C5-LLM1 C6-LLM1 C7-LLM1 TSOM-LM3
ABS-LLI1 ABS-LLP4 ABS-LLM3
maxilla
CRV_UI1 WNG_LI1 SHV_LI1 DSHV_LI1 IG_LI1
TD_LI1
CMR_LC CDAR_LC ME_LM1 HYP_LM1 C_5_LM1 CAR_LM1
PAR_LM1 PEG_LI2 PEG_LM3 ABS_LI2 ABS_LP4
ABS_LM3
MESIODENS
The trait reduction based solely on the idea of key teeth yielded very
different distance statistics. The
Euclidean cluster (Figure M) and distance matrix (Figure N) still showed
the Garasias as most closely related
to the Bhils and the Garasia were still most distant to the Rajputs.
However, in this analysis the Rajputs and
Bhils were most closely linked inside the larger cluster which related
to the Garasia. This relationship was
again confirmed by the Mean Measure of Divergence statistics (Figure
O).
Figure M Euclidean Distance Cluster for key teeth
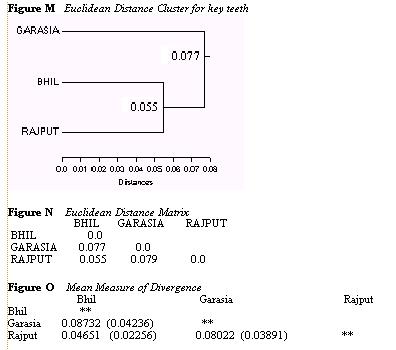
Figure N Euclidean Distance Matrix
BHIL GARASIA
RAJPUT
BHIL
0.0
GARASIA 0.077
0.0
RAJPUT
0.055 0.079
0.0
Figure O Mean Measure of Divergence
Bhil
Garasia
Rajput
Bhil
**
Garasia 0.08732 (0.04236)
**
Rajput 0.04651
(0.02256)
0.08022 (0.03891)
**
These tests from the key tooth reduction not only indicated a
different set of relationship between
the three groups, they also indicated a new level of distance. The
MMD now appears to suggest that the
Garasia are equally distant to the Bhils and the Rajputs, a figure
almost twice as large as the distance
between the Bhils and Garasias. Concern that these results conflicted
so greatly with the results obtained by
the original analysis with all of the traits, as well as uncertainty
about the usefulness of the criteria whereby I
had created this data reduction, forced me to step back and form a
new set of more useful criteria by which
to reduce the data before performing any more tests.
I decided that the reduction should account for 1.) significant
p-values in the chi-square test for
differences between the three groups, 2.) a presence frequency equal
to or greater than 30% for a given trait
in at least one population, and 3.) consideration of intra-class correlations.
The traits included in the third
(and final) analysis are given in Figure P. I performed the chi-square
test again to get revised p-values, given
the difference in expected counts with the new table.
Figure P Significant Traits with a >30% frequency in at
least one group
Test for significant differences between groups:
Presence Frequencies and Chi-square P-values (alpha = 0.05)
Raj-Bhl
Bhl Bhl-Grs
Grs Raj-Grs
Raj 3 Groups
trait
p-value
% p-value
% p-value
% p-value
Mandible
CNO-LLP3 0
91.346 0
85.149 0
78.125 0
CNO_LLP4 0.02
28.846 0.02
52.475 0
49.479 0.02
AFV-LLM1 0
44.231 0
57.426 0
63.542 0
GRV-LLM1 0
72.115 0
71.287 0
70.313 0
GRV-LLM2 0
81.731 0
79.208 0
78.646 0
CNO-LLM1 0
91.827 0
95.545 0
97.917 0
CNO-LLM2 0
91.827 0
91.584 0
91.667 0
C5-LLM1
0
80.288 0
82.178 0
82.813 0
Maxilla
CRV_UI1
0
72.115 0
75.124 0
68.269 0
SHV_LI1
0
86.538 0
82.09 0
78.846 0
SHV_LI2
0
61.058 0
46.766 0
50.962 0
SHV_LC
0
56.731 0
53.731 0
60.096 0
TD_LI1
0.001 46.154
0.001 45.274 0.001
45.673 0.001
TD_LC
0.006 52.885
0.001 41.294 0.007
34.615 0.007
CDAR_LC
0
66.827 0
68.159 0
59.615 0
ME_LM1
0
99.038 0
99.502 0
97.596 0
ME_LM2
0
89.423 0
87.562 0
86.538 0
HYP_LM1
0
99.519 0
99.005 0
98.558 0
HYP_LM2
0
85.577 0
82.587 0
75.962 0
C_5_LM2 0.028
26.923 0.071 12.935
0.042 87.5
0.071
CAR_LM1 0
56.731 0
49.254 0
68.75
0
Once again I calculated the Euclidean distance between the three
groups and the MMD. The
Euclidean distance cluster (Figure Q) positioned the Rajputs as most
distant, the Bhils and Garasias as
closest though the Garasia are not intermediate. Given the more meaningful
reduction criteria and the fact
that these results parallel those obtained in the original analysis,
I think that this reduction analysis is more
accurate than the reduction by key teeth. The Rajputs are almost
equidistant to the Garasia and the Bhils
(see Figures R and S) with a slightly closer relationship to the Bhils,
who are almost twice as close to the
Garasia.
Figure Q Euclidean Distance Cluster
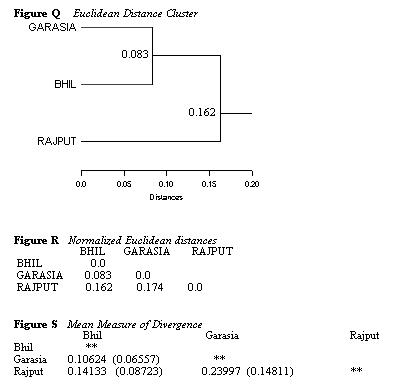
Figure R Normalized Euclidean distances
BHIL GARASIA
RAJPUT
BHIL
0.0
GARASIA 0.083
0.0
RAJPUT 0.162
0.174 0.0
Figure S Mean Measure of Divergence
Bhil
Garasia
Rajput
Bhil
**
Garasia 0.10624 (0.06557)
**
Rajput 0.14133
(0.08723)
0.23997 (0.14811)
**
To explain the variance between the three groups, I performed
a new principle components
analysis, one that appears more useful to me in explaining the variance
as it is not strictly divided along the
lines of individual teeth (see Figure T). Because of the reduced volume
of data, I was able to combine both
jaws into one analysis. Nine components had eigenvalues above one and
combined, they explain 65% of the
variance between the three groups.
Figure T Principle Components Analysis (no rotation)
Component loadings
Components
Traits
1 2
3
4
5
SHV_ULI2
0.753 0.111
0.155 0.194
0.053
SHV_ULC
0.749 0.014
-0.164 0.093
-0.088
SHV_ULI1
0.730 0.136
0.283 0.071
-0.071
TD_ULI1
0.564 0.269
-0.071 -0.103
-0.258
TD_ULC
0.520 0.173
0.152 0.109
0.078
CNO_LLM1
-0.393 0.665
0.027 0.312
-0.030
C_5_LLM1
-0.384 0.655
0.194 0.145
0.082
ME_ULM1
0.004 0.501
0.015 -0.394
-0.219
CAR_ULM1
0.055 -0.068
-0.121 -0.465
0.169
CNO_LLP4
0.071 -0.083
0.410 -0.015
0.349
GRV_LLM2
0.030 0.272
-0.128 0.367
-0.173
CRV_ULI1
0.004 -0.002
0.418 -0.191
-0.452
HYP_ULM1
0.272 0.235
-0.355 -0.404
0.175
CDAR_ULC
0.217 0.387
0.312 -0.019
0.150
HYP_ULM2
0.168 0.217
-0.392 -0.313
0.374
CNO_LLP3
-0.062 -0.011
0.426 0.005
0.492
C_5_ULM2
0.186 0.296
-0.148 0.162
0.427
AFV_LLM1
-0.169 0.371
-0.342 0.310
0.135
GRV_LLM1
0.134 -0.039
-0.363 0.330
-0.279
ME_ULM2
-0.136 0.491
-0.093 -0.415
-0.210
CNO_LLM2
-0.114 0.246
0.419 -0.152
-0.141
Variance explained 13.456 10.101
7.544 6.778
6.220
Components
Traits
6 7
8
9
SHV_ULI2
0.193 0.143
0.022 0.071
SHV_ULC
0.228 -0.008
0.008 -0.072
SHV_ULI1
0.004 -0.034
0.142 0.037
TD_ULI1
-0.016 0.019
0.020 0.050
TD_ULC
-0.288 0.343
0.036 -0.127
CNO_LLM1
0.128 0.231
0.071 0.042
C_5_LLM1
0.004 0.049
-0.050 0.154
ME_ULM1
-0.049 0.293
-0.123 -0.405
CAR_ULM1
0.624 -0.102
-0.144 0.229
CNO_LLP4
-0.046 0.257
-0.576 0.026
GRV_LLM2
-0.165 0.048
-0.181 0.580
CRV_ULI1
-0.030 -0.252
0.293 0.389
HYP_ULM1
-0.007 0.126
-0.215 0.341
CDAR_ULC
0.221 -0.481
-0.099 -0.217
HYP_ULM2
-0.436 -0.116
0.049 0.156
CNO_LLP3
0.301 0.142
0.290 0.156
C_5_ULM2
-0.287 -0.490
0.186 -0.109
AFV_LLM1
0.384 -0.056
0.045 -0.079
GRV_LLM1
0.199 -0.199
-0.386 -0.078
ME_ULM2
0.109 0.058
0.228 -0.077
CNO_LLM2
-0.162 -0.385
-0.453 -0.003
Variance explained 5.947
5.426 5.240
4.774
In the second trait reduction, the distance statistics from the
MMD calculation were narrower
which may be due to fewer possibilities for trait interactions. The
principle components analysis is also more
accurate to the real causes of variance when the third molar and other
teeth which were mostly absent were
not included. The third molar may have caused more variability because
eruption is not complete until early
adulthood and this tooth is most subject to environmental influence.
The final principle component analysis
suggests that the most variance between the three groups is explained
by morphology of the anterior teeth.
The contrast between anterior and posterior morphology in the component
analysis is similar to one of the
components of variance in the odontometric analysis (Hemphill and Lukacs,
1993).
The results of this study suggest that the Garasia are related
to both the Bhils and the Rajputs
though they are morphologically more similar to the Bhils. Though the
Garasias do not occupy an
intermediate position between the Bhils and the Rajputs, the results
do not definitively rule out the possibility
that they are descendants of the Rajputs with some genetic contribution
from the Bhils. Their closer
proximity to the Bhils could be related to environmental and status
differences between the Rajputs and the
other two groups, which are very pronounced and long-standing. The
use of discrete traits as a test of
genetic relatedness is complicated because the traits are phenotypic
representations of the genotype.
Additionally, the traits are estimated to have various modes of inheritance
and most do not fall into a simple
autosomal dominant-recessive model (Turner and Scott, 1997).
To further test the possibility that the Garasia are descendants
of the Rajputs with some admixture
from the Bhils, I used a model from population genetics. I calculated
the approximate allele frequencies for
the traits generally assumed to have a threshold model of dominant
inheritance (Turner and Scott, 1997).
The Protostylid, Carabelliís cusp, and Shovelling have an approximately
normal phenotypic distribution
above the threshold of expression, or in other words if the total presence
frequency is high it will have an
approximately normal distribution (ibid.). I used the chi-square test
(Figure U) to look at the fit between the
observed counts of present traits as compared to the expected Hardy-Weinberg
equilibrium counts (Hartl
and Clark, 1989). I used a model for one-way migration pt= p + ( po
- p )( 1 - m ) where po is a donor
population into p and pt is the proposed hybrid population (ibid.).
The model estimates the percentage of alleles donated by the
Bhils to the Rajputs per generation, if
the Garasia are a hybrid population from their union. The model is
based on the historical record that the
Garasias were hybrid descendants of both groups, whereby the Bhils
had donated women in a hypergynous
flow into unions with Rajput men. If the Rajputs began establishing
themselves in Gujarat in the 8th century
AD, the admixture potentially lasted for 1200 years (or 40 generations).
The Protostylid had a low presence
count and was not included in the model in the hopes of capitalizing
on the more normal distributions of the
other two traits with greater frequencies.
Figure U Goodness of Fit to Hardy-Weinberg Expectations
Counts and (Expected Values) (df= 4, alpha = 0.05)
Homozygous
Homozygous
Population Recessive
Heterozygous Dominant
X2
p-value
Protostylid M1 Grade 0
Grades 1-7
Grade 8
Bhils
159 (171.86)
34 (20.8)
0 (0.34)
9.68
p-value < 0.05
Garasias
185 (171.86)
8 (20.8)
0 (0.34)
9.23 0.05 < p-value < 0.10
Rajputs
160 (160.29)
19 (19.4)
1 (0.34)
1.46
p-value > 0.25
Shovelling I1 Grade 0
Grades 1-4
Grade 5
Bhils
19 (31.02)
180 (167.65)
0 (0.33)
5.90
p-value > 0.20
Garasias
34 (31.02)
165 (167.65)
0 (0.33)
0.66
p-value > 0.25
Rajputs
41 (31.96)
163 (172.70)
1 (0.34)
4.38
p-value > 0.25
Carabelli's M1 Grade 0
Grades 1-6
Grade 7
Bhils
89 (84.64)
118 (120.33)
0 (2.04)
2.32
p-value > 0.25
Garasias
99 (80.96)
99 (115.09)
0 (1.95)
8.22 0.05 < p-value < 0.10
Rajputs
61 (83.41)
137 (118.58)
6 (2.01)
10.83 0.025< p-value < 0.05
Using the migration model for Shovelling and Carabelliís trait
gave me low estimates for the Bhil
contribution to the Garasia heritage. To get the Garasias observed
count for Shovelling, the Bhils would
only have had to contribute 3.94 % of alleles per generation to the
Rajput gene pool. For Carabelliís trait,
the observed Garasia counts would indicate a negligible and insignificant
contribution from the Bhil gene
pool. The odontometric analysis positioned the Garasia as a hybrid
but they are probably not an even mix of
the Bhil and Rajput gene pools. I think that this analysis confirms
the descent relationship for the Garasias
and Rajputs but places the Bhils in the position of less genetic and
more environmental influences. The
cluster analysis in this study placed the Bhils as more intermediate.
The Bhils are most certainly not a hybrid
group between the Garasia and the Rajputs, therefore I believe that
the positioning and the accuracy of the
distance statistics were compromised by environmental influences which
positioned the Bhils and Garasia
closer together.
These results suggest that the Garasia could have been descendants
of tribalised Rajputs and/or of
some Bhil-Rajput unions whether through hypergynous flow or intermarriage.
The facts that the Garasia are
known in the historical record to have been occupying Gujarat as a
distinct group from at least the 18th
century and that their status is more similar to the Bhils and other
forest-dwelling peoples, give support to
their morphological similarities to the Bhils even if they once originated
from the Rajput lineage. The
distance statistics show a fairly close relationship between all three
groups and the one-way migration model
indicates that it would not require much admixture to produce the observed
patterns if the Rajput gene pool
was supplemented with a small generational contribution from the Bhils.
However, this model is based on
only two traits and has very specific assumptions which may not be
valid, such as the number of generations
in which admixture took place. More work will certainly be required
if the true nature of these relationships
is to be fully understood. Serological analysis, craniometrics, and
archaeology are all components which
have yet to be included in this discussion of the history and origin
of the people of Gujarat.