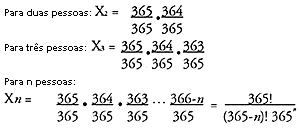"Você não acredita em telepatia?" Meu
amigo, um profissional sóbrio, pareceu surpreso.
"Você acredita?!" Eu perguntei. "Claro!
Muitas vezes em que eu estava na rua à noite e,
repentinamente, fiquei preocupado com meus filhos. Quando
ligo pra casa, fico sabendo que um deles está doente, se
machucou ou teve pesadelos. Que outra explicação você
tem pra isso?"
Tais episódios acontecem a todos nós e é comum
escutar as pessoas dizerem "Isto não pode ser só
coincidência." Atualmente a explicação que muitas
pessoas alcançam envolve telepatia ou habilidades
psíquicas. Mas será que nós devemos nos entregar assim
prontamente nos braços de um reino místico? Esses casos
não podem ser realmente coincidência?
Há dois fatos a respeito de coincidências que a
maioria das pessoas não conhece. Primeiro, nós tendemos
a reforçar o significado de coincidências, tanto
acordado como em sonhos, nas nossas memórias. Eventos
comuns, isto é, que não tem nada demais, não ficam
registrados em nossas memórias com a mesma intensidade.
Segundo, nós falhamos em compreender se os eventos
altamente improváveis que ocorrem todos os dias a todos
nós, são realmente difíceis de acontecer. É
impossível estimar as probabilidades dos eventos
coincidentes que ocorrem em nossas vidas diárias. Nós
freqüentemente tendemos a atribuir às coincidências
uma probabilidade menor do que elas tem de acontecer.
Entretanto, é possível calcular as probabilidades de
alguns eventos aparentemente improváveis com exatidão.
Esses exemplos fornecem pistas de como nossas
expectativas fogem da realidade.
Aniversários Coincidentes:
Em uma seleção aleatória de 23 pessoas há 50% de
chance de pelo menos duas delas fazerem aniversário no
mesmo dia. Quem não fica surpreso ao ouvir isso pela
primeira vez? O cálculo é exato. Primeiro calculamos a
probabilidade de todas as pessoas no grupo terem
aniversários diferentes (X) e então subtraímos esta
fração de 1 para obtermos a probabilidade de um
aniversário comum no grupo (P), P = 1 - X.
Probabilidades variam de 0 a 1, ou podem ser expressas de
0% para 100%. Para não haver aniversários coincidentes,
uma segunda pessoa tem uma escolha de 364 dias, uma
terceira pessoa tem 363 dias, e a enésima pessoa tem
(366 - n) dias. Assim a probabilidade para aniversários
diferentes fica:
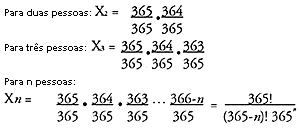
Com esses fatoriais a última equação não é
especialmente útil a menos que se tenha a habilidade de
calcular números grandes. Fica mais fácil usar um
computador para calcular Xn da primeira igualdade para
valores sucessivos de n. Quando n = 23, X = 0.493 e P =
0.507. Um gráfico da probabilidade de pelo menos um
aniversário em comum, P, versus o número de pessoas, n,
aparece no lado direito em círculos na Figura 1. A curva
mostra que a probabilidade de pelo menos duas pessoas
fazerem aniversário no mesmo dia cresce lentamente, a
princípio em menos de 12% com dez pessoas, aumentando
para 50% de probabilidade no círculo aberto
correspondente a vinte e três pessoas,
"achatando" alcançando 90% de probabilidade em
um grupo de quarenta uma pessoas. Isso significa que, na
média, de dez grupos aleatórios de quarenta e uma
pessoas, em nove deles pelo menos duas pessoas farão
aniversário no mesmo dia. Nenhumas força misteriosa é
necessária para explicar esta coincidência.
|
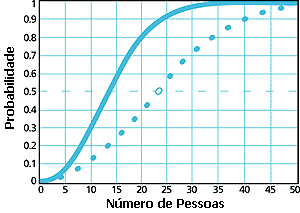
Figura
1. Probabilidades de Aniversários Coincidentes:
a curva de círculos à direita representa a
probabilidade de que em um grupo aleatório de
pessoas pelo menos duas façam aniversário no
mesmo dia. Como indicado pelo círculo aberto,
uma probabilidade de 50% é alcançada com
somente 23 pessoas. A curva à esquerda
representa a probabilidade que em um grupo
aleatório de pessoas pelo menos duas façam
aniversário em um dia, ou seja, em um período
de 24 horas. A probabilidade para esta
coincidência é de 50% ocorre com somente 14
pessoas.
|
Note que a probabilidade de aniversários coincidentes
para 23 + 23 = 46 pessoas não é 100%, como alguns
poderiam supor, mas 95% como mostrado pela curva à
direita na figura 1. Estendendo a curva além do limite
de Figura 1 revela-se que cinqüenta e sete pessoas
produzem 99% de probabilidade de aniversários no mesmo
dia.
O mesmo princípio pode ser usado para calcular a
probabilidade que em um grupo aleatório pelo menos duas
façam aniversário dentro de um dia (período de 24
horas, isto é, mesmo dia e dois dias adjacentes). Esta
condição é menos restritiva que a anterior, e 50% de
probabilidade é conseguida com somente catorze pessoas.
A curva à esquerda na figura 1 mostra o gráfico das
probabilidades de aniversário dentro de um dia.
Cavando um pouco mais fundo em alguns aspectos das
probabilidades de aniversários idênticos chegamos a
mais conclusões. Note que nós dissemos vários vezes
"pelo menos duas pessoas" fazendo aniversário
no mesmo dia. Conforme o tamanho de grupo aumenta as
chances para coincidências múltiplas também aumentam.
A curva que desce à esquerda da Figura 2 (pontilhada em
preto) representa a probabilidade de nenhuma
coincidências (NC) de aniversário, idêntico aos
valores do Xn calculados acima. A primeira curva com um
gráfico de máximo (bolinhas azuis) representa a
probabilidade de somente um par de pessoas (1P) fazendo
aniversário no mesmo dia. O máximo ocorre com vinte e
oito pessoas, tendo uma probabilidade de quase 39%.
Conforme o grupo aumenta, a probabilidade de outras
coincidências também aumenta. A segunda curva com um
máximo (de preto) representa a probabilidade de
exatamente dois pares de pessoas (2P) fazendo
aniversário no mesmo dia. Seu máximo ocorre com trinta
e nove pessoas, com uma probabilidade de 28%. A última
curva ascendendo na Figura 2 (pontilhada em azul)
representa todas as outras probabilidades de
coincidências (>2P), consistindo de três pares,
três pessoas, quatro pares, etc. Em qualquer ponto do
gráfico, as quatro curvas juntas totalizam 100% de
probabilidade.
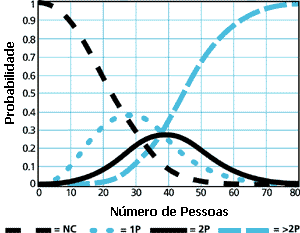 |
Figura 2.
Probabilidades de Múltiplos Aniversários
Coincidentes: A curva que desce à esquerda
representa a probabilidade de não haver nenhuma
coincidência (NC). A primeira de máximo
representa a probabilidade de apenas um par (1P)
com aniversário idêntico. A segunda curva de
máximo representa a probabilidade de exatamente
dois pares (2P) com aniversários idênticos
(data diferente para cada par). A curva que sobe
à direita representa as probabilidades de todas
outras coincidências (>2P), três pares,
três pessoas, quatro pares, etc. Para qualquer
número de pessoas as probabilidades das quatro
curvas totaliza 100%. |
A Figura 2 mostra que para vinte e três pessoas as
probabilidades são 36% para um par, 11% para dois pares,
e 3% para o total de todas as outras coincidências para
uma soma de probabilidades de 50%. Esses 50% são as
chances de haver pelo menos um tipo de coincidência.
Para vinte e três pessoas a probabilidade de nenhuma
coincidência também é de 50%, como mostrada na curva
que desce (NC) na Figura 2. Há uma quase interseção
tripla com trinta e oito pessoas onde as probabilidades
de 1 par idêntico, 2 pares idênticos, e o total de
todas outras coincidências está em 28-29%. Para trinta
e oito ou mais pessoas o total de todas outras
coincidências torna-se maior que a probabilidade de um
ou dois pares, e passa de 50% com quarenta e cinco
pessoas. Em um grupo aleatório de mais de quarenta e
cinco pessoas a maior probabilidade é de haver mais de
duas pessoas fazendo aniversário no mesmo dia.
Esta série de cálculos serve para tirarmos uma
conclusão: Se coincidências de datas de aniversários
são muito mais comuns do que poderíamos imaginar,
então provavelmente muitas daquelas outras
coincidências em nossas vidas são muito mais fáceis de
acontecer e não são tão fantásticas assim. Nós não
devemos multiplicar as hipóteses: o princípio da
"Lâmina de Occam" declara que a explicação
mais simples deve prevalecer.
Mãos de "Copas Fora"
No jogo de cartas chamado "Copas Fora" há
635.013.559.600 (seiscentos e trinta e cinco bilhões,
treze milhões, quinhentos e cinqüenta e nove mil e
seiscentas) mãos de treze cartas diferentes. Este
número de mãos podiam ser jogadas se todas as pessoas
do mundo tivessem jogado "Copas Fora" pelo
menos um dia. Para um indivíduo poderia levar vários
milhões anos jogando continuamente para que ele
recebesse cada uma destas mãos. Para um jogador tirar
qualquer mão a probabilidade é de 1/635.013.559.600 ou
um pouco mais que uma parte em um milhão de milhões.
Qualquer mão é tão improvável quanto tirar as treze
cartas de copas numa vez, mas toda vez que jogamos
pegamos alguma mão. Mãos de "Copas Fora" são
um exemplo de ocorrências diárias de eventos muito
improváveis, a única diferença é que não
determinamos antes quais cartas vamos tirar, por isso nem
notamos que aconteceu uma enorme coincidência.
Jogadas de "Cara ou Coroa"
Que seqüência de caras (C) e coroas
(O) você espera em vários lançamentos
aleatórios de uma moeda? Nem todas caras, nem todas
coroas, nem mesmo a seqüência alternada (OCOCOCOC),
já que esta série é obviamente regular e não
aleatória. Em uma seqüência aleatória nós esperamos
que saia tanto caras quanto coroas. Nós podemos simular
progressões de lançamentos de moeda com uma seqüência
aleatória de números.
Até onde se sabe, os dígitos decimais do número
irracional p, que multiplica o
diâmetro de um círculo para obter a circunferência,
são aleatórios. Isto não significa que toda vez que p é calculado dê um resultado
diferente, mas significa que o valor de qualquer dígito
é imprevisível a partir dos dígitos anteriores. Um
exemplo de um padrão previsível é a seqüência de
dígitos decimais na fração 1/7=0,142857142857142857. .
. , onde há uma óbvia repetição de todos os seis
dígitos decimais.
Os dígitos decimais de p
têm sido calculados para centenas de milhões de
dígitos por computadores muito velozes, mas nós
listamos aqui somente os primeiros 100 dígitos em quatro
filas de 25 dígitos.
3,1415926535897932384626433
8327950288419716939937510
5820974944592307816406286
2089986280348253421170679
Há cinqüenta e um dígitos pares e quarenta e nove
dígitos ímpares. Há quase uma distribuição igual
quando os primeiros 100 dígitos decimais são divididos
de outra maneira: quarenta e nove dígitos de 0 para 4 e
cinqüenta e um dígitos de 5 para 9.
Sabendo que os dígitos decimais de p são aleatórios, nós podemos
simular uma seqüência aleatória de caras e coroas em
lançamentos de moeda correspondendo dígitos pares para
caras e dígitos ímpares para coroas. A seqüência de
caras e coroas em 100 lançamentos com 25 lançamentos
por linha torna-se:
OCOOOCCOOOCOOOOCOCCCCCCOO
COCOOOCCCCCOOOOCOOOOOOOOC
OCCCOOCOCCOOCOCOCOCCCCCCC
CCCOOCCCCCOCCCOOCCOOOCCOO
Observando a seqüência aleatória nós encontramos
algumas regularidades, tal como a seqüência alterada de
oito lançamentos de 62-69 (sublinhado). A probabilidade
de uma seqüência alternada de 8 lançamentos é uma vez
em 128 lançamentos (dois elevado à sétima potência).
Há algumas seqüências longas só de caras e só de
coroas. Há duas seqüências de 5 caras, uma seqüência
de 6 caras, uma seqüência de 8 coroas, e uma
seqüência surpreendente de 10 caras. Os dígitos
decimais 69-78 de p são todos
pares (logo após os dígitos sublinhados). Uma
seqüência de dez dígitos pares deveria ocorrer
unicamente uma vez em 1.024 dígitos (dois elevado a
décima potência). Ainda assim uma seqüência dessas
ocorre nos primeiros oitenta dígitos.
Que temos aqui? Uma prova de que os dígitos decimais
de p não são aleatórios?
Não, o que nós temos em vez disso, é uma
demonstração de como sempre é possível combinar dados
aleatórios para encontrar regularidades não
determinadas anteriormente. Já que dez dígitos pares
ocorrem dentro dos primeiros 100 dígitos decimais de p,
nós podemos (erradamente) pensar que seqüências como
essa ocorrem freqüentemente. Na verdade outra
seqüência de dez dígitos pares não ocorre outra vez
nos primeiros 1.000 dígitos decimais de p. Nos primeiros 1.000 dígitos uma
seqüência única de dez dígitos ímpares ocorre de
411-420.
O ponto é que a própria natureza de aleatoriedade
assegura que combinando dados randômicos chegamos a
algum modelo, só que ele não foi especificado antes, é
por acaso. Se alguém encontra um modelo combinando dados
aleatórios, pode usar isto como uma hipótese para
investigação de mais dados, mas nunca tirar uma
conclusão geral disto. Em nosso exemplo nós descobrimos
(mas não previmos) dez dígitos pares dentro dos
primeiros 100 dígitos, mas isso não ocorre outra vez
nos próximos 900 dígitos. Para confirmação de uma
tendência, os dados de alvo devem ser previstos antes da
análise dos dados. Se um modelo inesperado surge depois
da análise dos dados, o modelo pode ser usado como uma
hipótese para obter e analisar um conjunto inteiramente
novo de dados.
A seqüência caras e coroas pode ser aplicada de
outras maneiras. Considere um cabeça de área de futebol
que acerta 50% de seus passes ou um jogador de
basquetebol que converte 50% de seus arremessos. Designe
caras (C) para um passe certo ou um arremesso que se
converte e coroa (O) para erro de passe ou de lançamento
da bola de basquete. Você verá que há seqüências
inteiras de "passes certos" (C) e outras de
erros. Muitas das boas e más fases de jogadores se devem
somente ao acaso, são aleatórias. O jogador "pé
quente" é na maioria das vezes uma ilusão que
aparece em dados aleatórios quando analisados sob o
ponto de vista apaixonado de um torcedor.
Falando claramente, coincidências improváveis
ocorrem todos os dias para todos, e essas coincidências
são na maior parte o resultado do acaso. Se o conjunto
de dados é bastante grande, coincidências com certeza
vão aparecer, como demonstramos com os primeiras 100
dígitos decimais de p. A
probabilidade de saírem cinco caras seguidas em três
lançamentos é de 3%, em 100 lançamentos a
probabilidade torna-se 96%. Embora aplicado em um
contexto diferente, a teoria de
Ramsey (Scientific
American, Julho 1990) declara que "Todo conjunto
grande de números, pontos ou objetos, necessariamente
contém um padrão altamente regular." Não é
preciso postular forças misteriosas para explicar
coincidências.
|
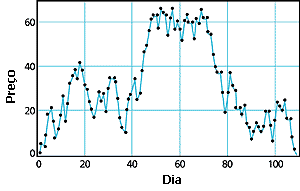
Figura 3.
Simulação De Mercado De Ações: Ação
simulada do mercado de ações em 109 dias de
negócio, gerada dos dígitos decimais
aleatórios de p. Este gráfico foi demonstrado
estar consistente com o jogo aleatório do
mercado de ações. Certamente, o número de dias
é flexível, um dígito decimal pode representar
qualquer fração ou número de dias. Veja a nota
no final do artigo para uma descrição de como
os preços das ações foram gerados. |
Preços Aleatórios no Mercado De Ações
Dado a fascinação corrente com o mercado de ações,
nós podemos gerar um resultado ainda mais interessante
dos dígitos decimais aleatórios de p.
Colocando no eixo x o número do dígito decimal e no
eixo y um valor de preço que é gerado a partir dos
dígitos decimais como descrito na Figura 3 e na nota no
final do artigo, de modo que há um equilíbrio
arbitrário entre altos e baixos do preço. Para os
primeiros 108 dígitos decimais de p
o gráfico todo está em território positivo. Começando
em zero o gráfico vai aumentando valores positivos,
atingindo um platô do 48-71 dígitos decimais antes de
começar a cair, quase voltando para zero no 99o
(nonagésimo nono) dígito, e cruzando o território
negativo depois do 108o (centésimo oitavo) dígito
decimal. Para um analista técnico de mercado de ações
este gráfico representa um gráfico típico de preços
das ações versus o tempo. Só que este gráfico foi
gerado dos primeiros 109 dígitos decimais aleatórios de
p! Disso podemos concluir que
as altas e as baixas são puramente aleatórias.
Um sorteio recente enviado por correspondência
oferecia um prêmio grande de $5.000.000 (cinco milhões
de dólares). A carta-resposta declarava que a
probabilidade de ganhar o prêmio era de um em
200.000.000. De todas as pessoas que receberam a
correspondência alguma ganhará o prêmio. Com tão
incrivelmente desfavorável probabilidade cada pessoa
deve decidir se vale a pena perder tempo e gastar um selo
postal para retornar a correspondência e participar. O
grande vencedor parece ser o serviço de correios, que
acumula mais que dez vezes o prêmio em selos vendidos.
Assim, da próxima vez você escutar "Isto não
pode ser só uma coincidência!" você terá muitas
justificativas para responder: "Por quê não?"
Reconhecimento
Agradeço ao Professor Russell N. Grimes da
Universidade de Virginia pelas discussões que tivemos e
que conduziram a Figura 2.
Nota
A ação de preço foi gerada em uma direção
positiva quando o dígito precedente é ímpar (exceto
para 5) e em uma direção negativa quando o dígito
precedente é par, com a grandeza do aumento ou
diminuição dada pelo valor do dígito. Assim dígitos
ímpares precedentes 1 + 3 + 7 + 9 = 20 gera uma
direção positiva e dígitos pares precedentes 0 + 2 + 4
+ 6 + 8 = 20 uma direção negativa. A soma das duas
direções é zero. Para o dígito 5 a direção está
para cima ou abaixo dependendo se o dígito prévio é
ímpar ou par ou até mesmo, respectivamente. Nos
primeiros 108 dígitos decimais há oito dígitos 5, cada
metade deles (quatro) gerando direções negativas e
positivas. Portanto temos um equilíbrio perfeito e
arbitrário entre as direções negativas e positivas.
Referências
Epstein, Richard Um. 1967. The
Theory of Gambling and Statistical Logic Nova
Iorque: Imprensa Acadêmica.
Falk, Ruma. 1981. On coincidences. Skeptical Inquirer
6(2): Inverno: 18-31.
Graham, Ronald L., e Joel H. Spencer. 1990. Ramsey
Theory. Scientific
American 263 (1): 112-117 (Julho).
Paulos, John Allen. 1988. Innumeracy.
Nova Iorque: Random House.
Weaver, Warren. 1963. Lady
Luck. Cultive Cidade, NY: Ancore Livros.
Bruce Martin é Professor Emérito de Química na
Universidade de Virginia, Charlottesville, Virginia.
voltar
Este artigo foi publicado por "Skeptical
Inquirer", número XX e foi adaptado para a língua
portuguesa e, especialmente, para a realidade brasileira,
tendo inclusive tido suprimidas certas partes que não
têm nenhuma relação cultural com os países de língua
portuguesa. Toda a responsabilidade pela tradução é de
Mauro Roberto de Pennafort