LinkExchange Member

Free Home Pages at GeoCities

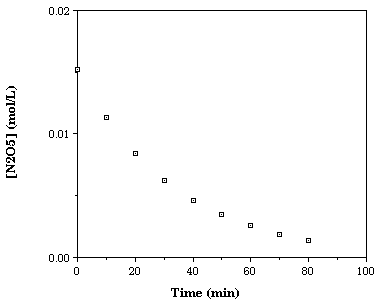
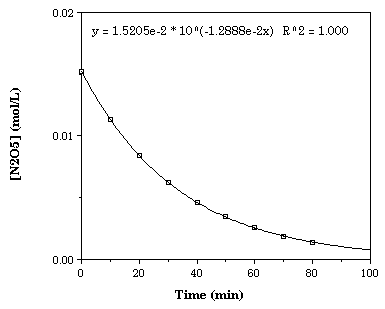
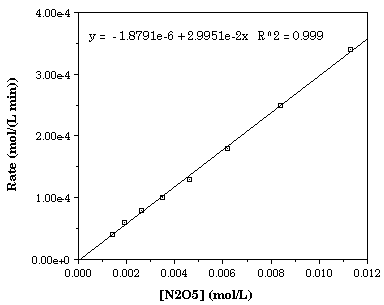
First Order Kinetics

We want to confirm that the decomposition of dinitrogen pentaoxide is a first order process. We will use a spreadsheet, and some calculus.

2N₂O₅(g) --> 4NO₂(g) + 0₂(g)

If the reaction is first order, it will fit the formula

Rate = k [N₂O₂]

Time (minutes)	[N2O5] (mole L-1)
0	0.0152
10	0.0113
20	0.0084
30	0.0062
40	0.0046
50	0.0035
60	0.0026
70	0.0019
80	0.0014

The above data was put into a spreadsheet, with the first column for time, and the second column for concentration.



The spreadsheet was told to data in the second column as a function of the data in the first column.



Next the spreadsheet was used to plot a "best-fit" exponential function through the data points.



The spreadsheet gives the function that provided curve for the "best-fit". The variable R² (shown as R^2) indicates how closes the "best-fit" function matches the data. Increasing R corresponds to better fits. A perfect fit will have R²=1.

The equation given above is in an obscure, unsatisfactory format.

We want an equation with two constants, one in front of the exponential, and the other inside the exponential next to the variable.

y = a e^bx

We can take the derivative of the above function.
This will give us a function that provides the reaction rate as a function of time.

Microsoft Excel provides the function

y = 0.0152 e^-0.0297x

We now need to know how to take the derivative of a function a e^-bx.

The derivative of a e^bx is

(ab) e^bx

Thus, the derivative of 0.0152 e^-0.0297x is

(0.0152 * -0.0297) e^-0.0297x

Homework problem:

Use a spreadsheet to calculate reaction rate as a function of time.

1. Put the time values in the first column.
2. Use the second column to calculate the reaction rate using the above function.

Put the concentrations in a third column.

Plot the second column (reaction rate) as a function of the third column (concentration).

Your graph should resemble what is shown below:



In looking at the above graph, it will become apparent that the computer program generating the graph puts in the 'e' to signify exponent.

This is a bad thing to do! Typically 'e' signifies 2.718281828..., a number which has a significance as important as pi (3.1415926...).




Next Page

Return to Master Alchemist Index



Last Revised 02/03/98.
Copyright ©1998 by William L. Dechent. All rights reserved.