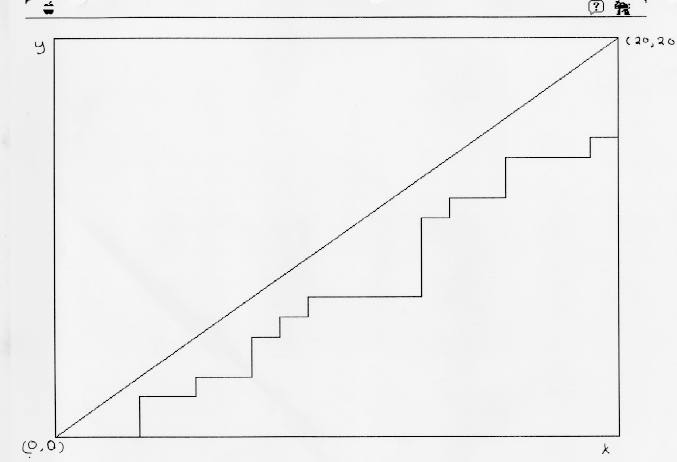
This is a computer program I wrote to plot our data on a graph. Basically, it takes all the numbers that we got for either bowline and puts them in order from lowest to highest. It then gives them out. If a number is given to the right-handed bowline, a point is drawn one over on the x-axis. If a number is given to the left-handed bowline, a point is drawn one up on the y-axis. In this way, the path makes its way to 20,20, because in the end both bowlines will have twenty results. I put the data in the program using 0s and 1s, a 0 denoting a result belonging to the right-handed bowline and a 1 denoting a result belonging to the left-handed bowline.

This is the graph I received from the program I wrote to graph my data. It will be noticed that it stays below a line drawn directly from 0 to 20. This is because at no time had the left-handed bowline been given the same amount or more cards than the right-handed bowline. It always had less, because the data was given out from the smallest, and the left-handed bowline had more large numbers than small numbers.
randomize
This is a program I wrote to draw the same type of graph as the other program, but this time for random numbers. If the path were to stay below the line, as it did in the last graph, it would mean that the y-axis always had greater numbers when the data was sorted. I do not specify if the y-axis or x-axis is supposed to represent a certain bowline. This path would end up under the line if either bowline, when the data was sorted, always had larger results.
This is the graph I received from my last program. It will be seen that the graph crossesover and under the line a number of times. this is because, at some point, both the x-axis and the y-axis had the same amount of numbers given to them, or because at some time the x-axis, the axis that got the first number, had less numbers than the y-axis. This means that, when sorted, one owuld not always have the larger numbers.
randomize
This is another program I wrote that does the same thing as the last program. However, it does not show the graph. It does my last program one million times over, and sees each time if the line is touched. The result, as can be seen, was 974659. That means that was the number of times the line was touched out of one million times. It also means taht about 97.4% of the time, the line will be touched. It is only about 2.6% of the time that the line will not be touched, except at the starting and ending points. My data belongs to that 2.6% of the time. Since this 97.4% surpasses the 95% confidence level that statisticians need to accept something as evidence, this proves that the left-handed bowline can in general hold more weight before breaking than the right-handed bowline.
set window -1,21,-1,21
plot 0,0; 20,0; 20,20; 0,20; 0,0; 20,20
let y= 0
for l=1 to 39
if rnd > (20-y)/(40-(x+y)) then
let x= x+1
plot x,y;
else
let y= y+1
plot x,y;
end if
next l
end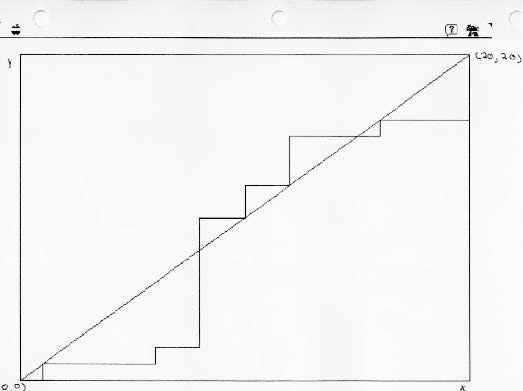
let s=o
for k= 1 to 1000000
let w= 0
let x= 1
let y= 0
for l=1 to 38
if rnd > (20-y)/(40-(x+y)) then
let x= x+1
else
let y= y+1
end if
if y>=x then
let w =1
end if
next l
if w=1 then
let s= s+1
end if
next k
print s