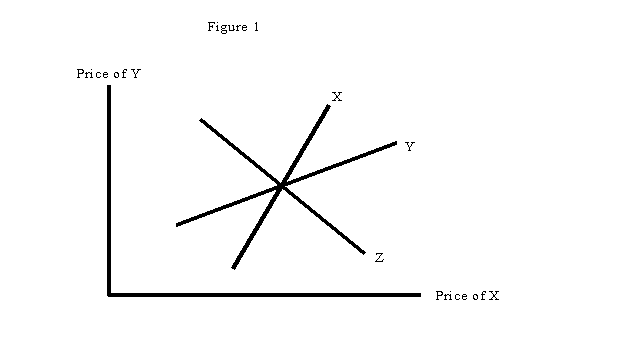
THERE'S SOMETHING ABOUT MACROIt's holiday season, and my thoughts have turned to ... course preparation. Classes don't begin until February, but books must be ordered, reading packets must receive copyright clearance and go to Graphic Arts, and background notes must be prepared.
This spring I have a new assignment: to teach Macroeconomics I for graduate students. Ordinarily this course is taught by someone who specializes in macroeconomics; and whatever topics my popular writings may cover, my professional specialties are international trade and finance, not general macroeconomic theory. However, MIT has a temporary staffing problem, which is itself revealing of the current state of macro, and I have been called in to fill the gap.
Here's the problem: Macro I (that's 14.451 in MIT lingo) is a quarter course, which is supposed to cover the "workhorse" models of the field - the standard approaches that everyone is supposed to know, the models that underlie discussion at, say, the Fed, Treasury, and the IMF. In particular, it is supposed to provide an overview of such items as the IS-LM model of monetary and fiscal policy, the AS-AD approach to short-run versus long-run analysis, and so on. By the standards of modern macro theory, this is crude and simplistic stuff, so you might think that any trained macroeconomist could teach it. But it turns out that that isn't true.
You see, younger macroeconomists - say, those under 40 or so - by and large don't know this stuff. Their teachers regarded such constructs as the IS-LM model as too ad hoc, too simplistic, even to be worth teaching - after all, they could not serve as the basis for a dissertation. Now our younger macro people are certainly very smart, and could learn the material in order to teach it - but they would find it strange, even repugnant. So in order to teach this course MIT has relied, for as long as I can remember, on economists who learned old-fashioned macro before it came to be regarded with contempt. For a variety of reasons, however, we can't turn to the usual suspects this year: Stan Fischer has left to run the world, Rudi Dornbusch is otherwise occupied, Olivier Blanchard is department head, Ricardo Caballero - who is a bit young for the role, but can swallow his distaste if necessary - is on leave. All of which leaves me.
Now you might say, if this stuff is so out of fashion, shouldn't it be dropped from the curriculum? But the funny thing is that while old-fashioned macro has increasingly been pushed out of graduate programs - it takes up only a few pages in either the Blanchard-Fischer or Romer textbooks that I am assigning, and none at all in many other tracts - out there in the real world it continues to be the main basis for serious discussion. After 25 years of rational expectations, equilibrium business cycles, growth and new growth, and so on, when the talk turns to Greenspan's next move, or the prospects for EMU, or the risks to the Brazilian rescue plan, it is always informed - explicitly or implicitly - by something not too different from the old-fashioned macro that I am supposed to teach in February.
Why does the old-fashioned stuff persist in this way? I don't think the answer is intellectual conservatism. Economists, in fact, are in general neophiles, always looking for something radical and different. Anyway, I have seen over and over again how young economists, trained to regard IS-LM and all that with contempt if they even know what it is, find themselves turning to it after a few years in Washington or New York. There's something about primeval macro that pulls us back to it; if Hicks hadn't invented IS-LM in 1937, we would end up inventing it all over again.
But what is it that makes old-fashioned macro so compelling? To answer that question, I find it helpful to think about where it came from in the first place.
Afficionados know that much of what we now think of as Keynesian economics actually comes from John Hicks, whose 1937 article "Mr. Keynes and the classics" introduced the IS-LM model, a concise statement of an argument that may or may not have been what Keynes meant to say, but has certainly ended up defining what the world thinks he said. But how did Hicks come up with that concise statement? To answer that question we need only look at the book he himself was writing at the time, Value and Capital, which has in a low-key way been as influential as Keynes' General Theory.
Value and Capital may be thought of as an extended answer to the question, "How do we think coherently about the interrelationships among markets - about the impact of the price of hogs on that of corn and vice versa? How does the whole system fit together?" Economists had long understood how to think about a single market in isolation - that's what supply-and-demand is all about. And in some areas - notably international trade - they had thought through how things fitted together in an economy producing two goods. But what about economies with three or more goods, where some pairs of goods might be substitutes, others complements, and so on?
This is not the place to go at length into the way that Hicks (and others working at the same time) put the story of "general equilibrium" together. But to understand where IS-LM came from - and why it continues to reappear - it helps to think about the simplest case in which something more than supply and demand curves becomes necessary: a three good economy. Let us simply call the goods X, Y, and Z - and let Z be the "numeraire", the good in terms of which prices are measured.
Now equilibrium in a three-good model can be represented by drawing curves that indicate combinations of prices for which each of the three markets is in equilibrium. Thus in Figure 1 the prices of X and Y, both in terms of Z, are shown on the axes. The line labeled X shows price combinations for which demand and supply of X are equal; similarly with Y and Z. Although there are three curves, Walras' Law (if all markets but one are in equilibrium, that market is in equilibrium too) tells us that they have a common intersection, which defines equilibrium prices for the economy as a whole. The slopes of the curves are drawn on the assumption that "own-price" effects are negative, cross-price effects positive - thus an increase in the price of X increases demand for Y, driving the price of Y up, and vice versa; it is also, of course, possible to introduce complementarity into such a framework, which was one of its main points.
This diagram is simply standard, uncontroversial microeconomics. What does it have to do with macro?
Well, suppose you wanted a first-pass framework for thinking coherently about macro-type issues, such as the interest rate and the price level. At minimum such a framework would require consideration of the supply and demand for goods, so that it could be used to discuss the price level; the supply and demand for bonds, so that it could be used to discuss the interest rate; and, of course, the supply and demand for money.
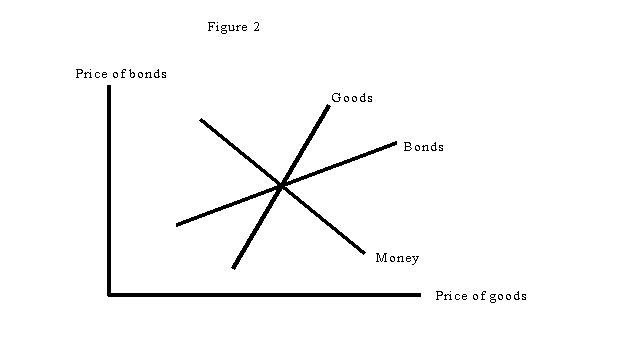
What, then, could be more natural than to think of goods in general, bonds, and money as if they were the three goods of Figure 1? Put the price of goods - aka the general price level - on one axis, and the price of bonds (1 divided by 1+i, if they are one-period bonds) on the other; and you have something like Figure 2 - or, more conventionally putting the interest rate instead of the price of bonds on the vertical axis, something like Figure 3 . And already we have a picture that is essentially Patinkin's flexible-price version of IS-LM.
If you try to read pre-Keynesian monetary theory, or for that matter talk about such matters either with modern laymen or with modern graduate students who haven't seen this sort of thing, you quickly realize that this seemingly trivial formulation is actually a powerful tool for clarifying thought, precisely because it is a general-equilibrium framework that takes the interactions of markets into account. Here are some of the things it suddenly makes clear:
1. What determines interest rates? Before Keynes-Hicks - and even to some extent after - there has seemed to be a conflict between the idea that the interest rate adjusts to make savings and investment equal, and that it is determined by the choice between bonds and money. Which is it? The answer, of course - but it is only "of course" once you've approached the issue the right way - is both: we're talking general equilibrium here, and the interest rate and price level are jointly determined in both markets.
2. How can an investment boom cause inflation (and an investment slump cause deflation)? Before Keynes this was a subject of vast confusion, with all sorts of murky stuff about "lengthening periods of production", "forced saving", and so on. But once you are thinking three-good general equilibrium, it becomes a simple matter. When investment (or consumer) demand is high - when people are eager to borrow to buy real goods - they are in effect trying to shift from bonds to goods. So as shown in Figure 4 , both the bond-market and goods-market equilibrium schedules, but not the money-market schedule, shift; and the result is both inflation and a rise in the interest rate.
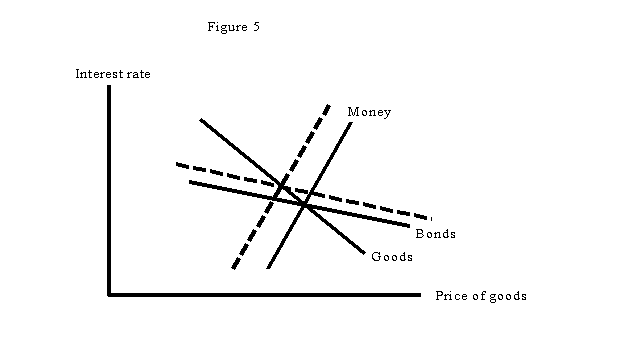
3. How can we distinguish between monetary and fiscal policy? Well, in a fiscal expansion the government sells bonds and buys goods - producing the same shifts in schedules shown in Figure 4. In a monetary expansion it buys bonds and "sells" newly printed money, shifting the bonds and money (but not goods) schedules as shown in Figure 5 .
Of course, this is all still a theory of "money, interest, and prices" (Patinkin's title), not "employment, interest, and money" (Keynes'). To make the transition we must introduce some kind of price-stickiness, so that incipient deflation is at least partly translated into output decline; and then we must consider the multiplier impacts of that output decline, and so on. But the basic form of the analysis still comes from the idea of a three-good general-equilibrium model in which the three goods are "goods in general", bonds, and money.
Sixty years on, the intellectual problems with doing macro this way are well known. First of all, the idea of treating money as an ordinary good begs many questions: surely money plays a special sort of role in the economy. Second, almost all the decisions that presumably underlie the schedules here involve choices over time: this is true of investment, consumption, even money demand. So there is something not quite right about pretending that prices and interest rates are determined by a static equilibrium problem. (Of course, Hicks knew about that, and was quite self-conscious about the limitations of his "temporary equilibrium" method). Finally, sticky prices play a crucial role in converting this into a theory of real economic fluctuations; while I regard the evidence for such stickiness as overwhelming, the assumption of at least temporarily rigid nominal prices is one of those things that works beautifully in practice but very badly in theory.
But step back from the controversies, and put yourself in the position of someone who must reach a judgement about the likely impact of a change in monetary policy, or an investment slump, or a fiscal expansion. It would be cumbersome to try, every time, to write out an intertemporal-maximization framework, with microfoundations for money and price behavior, and try to map that into the limited data available. Surely you will find yourself trying to keep track of as few things as possible, to devise a working model - a scratchpad for your thoughts - that respects the essential adding-up constraints, that represents the motives and behavior of individuals in a sensible way, yet has no superfluous moving parts. And that is what the quasi-static, goods-bonds-money model is - and that is why old-fashioned macro, which is basically about that model, remains so useful a tool for practical policy analysis.