Responsables scientifiques : Pavel KOULEV, Titaïna LEGRAND Suivi linguistique : Francine DANIN

1. Introduction *

2. Aspect théorique *

3. Aspect pratique *

4. Conclusion *

5. Bibliographie *

Figure 1. Figure de speckle. *

Figure 2. Ondes sphériques formées par une surface rugueuse. *

Figure 3. Système optique d?observation du speckle subjectif. *

Figure 4. Différence de chemin optique avant et après une déformation. *

Figure 5. Montage type de TV holographie dans le plan. *

Figure 6. Variations de l?intensité en fonction de la tension piézo. *

Figure 7. Axe de mesure. *

Figure 8. Calcul du vecteur de sensibilité. *

Figure 9. Rondelle en aluminium. *

Figure 10. Contrainte exercée sur la rondelle. *

Figure 11. Le montage d?origine. *

Figure 12. Directions d?éclairement de la rondelle. *

Figure 13. Fixation de la caméra. *

Figure 14. Schéma optique modifié. *

Figure 15. Eclairage de la rondelle. *

Figure 16. Support de caméra avec un troisième pied. *

Figure 17. Courbe de recherche de tension. *

Figure 18. Filtrage d?image phasée. *

Figure 19. Démodulation d?une image phasée. *

Figure 20. Vecteurs de déplacement. *

Figure 21. Cartes des phases. *

Figure 22. Masque de la rondelle. *

Figure 23. Franges d?interférences. *

Figure 24. Carte des déplacements *

Figure 25. Vecteurs de déplacement dans le plan. *

Figure 26.Cartes des déformations. *

Figure 27. Franges d?interférence avec un défaut. *

Figure 28. Cartes des déplacements avec un défaut. *

Figure 29. Vecteurs de déplacement dans le plan, avec défaut. *

1. Introduction

1. Aspect théorique

1. Le speckle

Lorsqu?on éclaire une surface rugueuse avec un laser, on observe une figure granulaire ou " speckle pattern " en anglais (Figure 1). Ce phénomène est dû aux propriétés particulières de cohérence de la lumière laser.



Figure 1. Figure de speckle.

Le speckle est un phénomène d?interférence à ondes multiples, en effet, la lumière diffusée par la surface rugueuse crée un champ d?ondes stationnaires constitué d?une superposition de champs d?amplitudes aléatoires provenant des différents points de la surface. Bref, on peut considérer tous les points de la surface comme des sources secondaires d?ondes sphériques (principe de Huygens) dont les phases varient en fonction du point dont elles sont issues (Figure 2). L?amplitude en un point de l?espace est donc la somme des amplitudes de chaque onde sphérique en ce point.

La taille de ces grains de speckle varie en fonction des conditions d?observation. En l?absence d?optique supplémentaire (c?est à dire que l?on enregistre les speckles directement sur un film ou sur un capteur) on observe le speckle objectif. La taille moyenne des grains de speckle objectif d est donnée par la formule (1).



Figure 2. Ondes sphériques formées par une surface rugueuse.

(1)

Longueur d?onde du laser

Distance entre la surface et l?écran

Diamètre du faisceau d?éclairement

En pratique, la mise en place d?un système optique de formation d?image modifie la superposition des ondes et conduit alors à une taille de grain différente, c?est le speckle subjectif. Dans le cas le plus simple (Figure 3) la taille moyenne des grains de speckle subjectif d est donnée par la formule (2) :

(2)

Longueur d?onde du laser

Grandissement du système d?observation L

Distance focale de la lentille d?observation L

Diamètre de la lentille d?observation L (ou du diaphragme du système)



Figure 3. Système optique d?observation du speckle subjectif.

Lorsque le diaphragme augmente, la quantité d?ondes qui interfèrent augmente et donc la taille du grain diminue.

Dans les cas habituels, la figure de speckle résultant de la réflexion diffuse de la lumière laser est un phénomène perturbant. Cependant cette figure est relativement sensible à un déplacement dans le plan de la surface objet (elle se décale en même temps que l?objet réfléchissant et s?approche donc d?un phénomène d?interférométrie). C?est cette propriété qui est exploitée en holographie de speckle (technique qui permet de remonter à la déformation à partir de la figure de speckle).

2. Principe de l?interférométrie de speckle

Lorsque l?on observe une surface éclairée par un laser, on voit les grains de speckle. Ces derniers dépendent de l?état de la surface : si cet état change, la figure granulaire change également. Logiquement, en comparant deux figures successives enregistrées avant et après une déformation, on doit pouvoir observer toutes les variations (déplacements ou déformations) de la surface. Ces changements dans la figure granulaire sont dus à des variations de phase : sur le deuxième enregistrement, la lumière va être diffusée par une autre aspérité de la surface et donc va parcourir un chemin différent (voir Figure 4).



Figure 4. Différence de chemin optique avant et après une déformation.

Ainsi, pour mesurer le déplacement en chaque point, il faut réaliser une carte des phases avant la déformation et une après, les soustraire et remonter par le calcul (connaissant les conditions d'éclairage et d?observation) aux mouvements.

3. La mesure de déformation dans le plan

Notre montage ne nous permet de mesurer que des déplacements dans le plans de la surface étudiée, c?est pourquoi nous ne détaillerons que cette méthode dans la suite de ce rapport. Il est bien sûr possible, avec un système différent du notre, de faire des mesures hors - plan.

1. Principe de la mesure

1. Système d?éclairage

Pour mesurer des déformations dans le plan, il faut utiliser un montage du même type que celui présenté sur la Figure 5.

Le système d?observation est composé d?une caméra CCD et de son objectif, le tout relié a un ordinateur. L?échantillon est une rondelle.

La rondelle est éclairé par deux faisceaux laser étendus issus de la même source. L?un d?eux est réfléchit par un miroir monté sur un dispositif piézo-électrique afin de pouvoir faire varier son chemin optique et donc son déphasage. C?est le système EOH : Electro-Optic Holography.



Figure 5. Montage type de TV holographie dans le plan.

2. Calcul de la carte des phases et des déplacements

Si l?on applique une tension linéaire au miroir piézo-électrique et que l?on relève l?intensité d?un point de l?échantillon, on observe une variation quasi-sinusoïdale (voir Figure 6) qui est le résultat de l?interférences des deux faisceaux d?éclairage.



Figure 6. Variations de l?intensité en fonction de la tension piézo.

Le déplacement du cristal piézo-électrique n?est pas parfaitement linéaire, surtout dans les basses tensions. Il vaut donc mieux travailler avec de hautes tensions.

Grâce à cette variation de chemin optique, l?ordinateur va pouvoir calculer la carte des phases qui représente la phase en chaque point de la rondelle. Pour cela, on suppose que les deux faisceaux ont la même intensité. Quatre images vont êtres prises en introduisant à chaque fois un déphasage supplémentaire de 90° à l?aide du miroir piézo-électrique. Cela nous donne les intensités suivantes :

(3)

(4)

(5)

(6)

A partir de ces quatre équations, on va pouvoir déterminer la phase initiale j de la manière suivante :

(7)

(8)

Ainsi, grâce à l?équation (8), l?ordinateur nous donne une image de la phase en tous points de la rondelle. Avant la déformation, j =j ₀ et après la déformation : j =j ₀+D j . Pour calculer D j , on va simplement soustraire les deux cartes des phases. L?image obtenu, est la figure résultant de l?interférence des deux images : elle représente, en chaque point, le déplacement relatif subit par ce dernier. Il suffit de définir un point de déplacement nul pour obtenir la carte des déplacement absolus. Ces derniers ne sont définis que pour un axe, celui qui est donné par l?intersection du plan d?incidence et du plan de la rondelle (Figure 7. Axe de mesure.).



Figure 7. Axe de mesure.

Cet axe est caractérisé par un vecteur sensibilité qui définit le vecteur unitaire de la mesure.

2. Vecteur sensibilité



Figure 8. Calcul du vecteur de sensibilité.

Le déphasage entre la position initiale M et la position finale M? (voir Figure 8) est définie par :

(9)

d : différence de marche

: vecteur sensibilité

: vecteur déplacement

(10)

(11)

(12)

On constate donc que la sensibilité suivant une direction dépend du module du vecteur de sensibilité qui dépend de l?angle d?incidence q des faisceaux d?éclairage. Ainsi, pour obtenir des mesures de haute sensibilité, il faut que la rondelle soit éclairée par des faisceaux rasants.

4. Un point de mécanique

La pièce que l?on étudie est une rondelle en aluminium (Figure 9). Son épaisseur e est de 3,2 mm, le diamètre intérieur d est de 12,5 mm et le diamètre extérieur D est de 45 mm.



Figure 9. Rondelle en aluminium.

Cette rondelle est sollicitée à la compression simple c?est-à-dire qu?elle est soumise à deux forces directement opposées, appliquées sur deux points diamétralement opposées (Figure 10).



Figure 10. Contrainte exercée sur la rondelle.

La contrainte exercée est donnée par l?équation (3).

(13)

est la force et est la surface sur laquelle on exerce la force.

La déformation résultante de cette contrainte est donnée par l?équation (4)

(14)

est le module d?Young du matériau déformé.

2. Aspect pratique

Une fois la partie théorie étudiée, nous avons tenté de faire des mesures avec le montage mis à notre disposition. Différents problèmes se sont présentés, nous avons du le modifier afin de les éviter et d?optimiser nos mesures.

1. Le montage

1. Le montage d?origine

1. Le schéma

Le montage optique mis à notre disposition au départ se présente de la façon suivante (Figure 11. Le montage d?origine.).



Figure 11. Le montage d?origine.

Notre système est sensible aux déformations dans l?axe d?éclairement. Pour obtenir une cartographie des déformations dans le plan de la rondelle, il est nécessaire d?éclairer successivement cette rondelle dans deux directions orthogonales l?une de l?autre. Pour cela il suffit de tourner les deux miroirs pivotants pour choisir la direction d?éclairement de la rondelle (Figure 12).



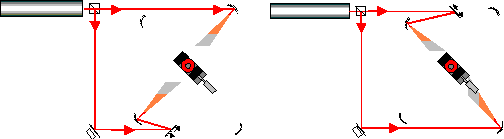
a)Eclairage suivant X. b)Eclairage suivant Y.

Figure 12. Directions d?éclairement de la rondelle.

Pour obtenir la carte des phases dans le plan, (voir paragraphe 2.3.1.2, page *) on enregistre la carte des phases dans chaque directions. Le calcul de la carte se fait à partir des images obtenues à l?aide d?une caméra CCD perchée au dessus de l?étau (voir Figure 13).



Figure 13. Fixation de la caméra.

2. Les problèmes

1. Les vibrations

Le montage d?holographie de speckle numérique est très sensible à toutes les variations de chemin optique que subissent les faisceaux. Il est donc très sensibles aux vibrations. Dès que quelqu?un marche dans la salle, les vibrations qu?il provoque influent sur les mesures ; il en est de même pour la soufflerie de la salle qui provoque des mouvements d?air très importants.

2. Les miroirs pivotants

Le montage utilise des miroirs pivotants. Ces derniers ont un léger jeu qui fait que le faisceau change légèrement de position à chaque rotation. Cela nous oblige à ajuster le montage après chaque rotation, ce qui ne facilite pas les mesures et les rend même parfois impossibles.

2. Le montage utilisé

1. Le schéma



Figure 14. Schéma optique modifié.

Nous avons réaliser un montage plus stable en remplaçant les miroirs rotatifs par des cubes séparateurs. Pour prendre une mesure en X, il suffit de couper les faisceaux Y1 et Y2 et pour prendre une mesure en Y, il suffit de couper les faisceaux X1 et X2 (voir Figure 14 et Figure 15).



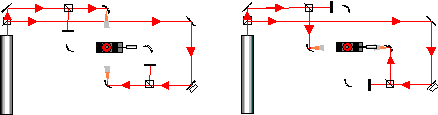
a)Eclairage suivant X. b)Eclairage suivant Y.

Figure 15. Eclairage de la rondelle.

2. Les améliorations

1. La chasse aux vibrations

La table mise à notre disposition a les pieds plantés dans le sol et solidaires du plancher flottant. Elle était bancale, il a fallut ajouter du sable.

Le montage est vissé sur une plaque nid d?abeille qui était directement posée sur la table. Nous avons intercaler entre les deux des chambres à air pour atténuer les vibrations.

La soufflerie faisait vibrer les câbles qui relient le montage (miroir piézo-électrique et caméra CCD), pour éviter cela, nous les avons fixé sur la table avec des bandes adhésives. De plus, pour stabiliser la caméra, nous avons ajouté un troisième pied à son support.



Figure 16. Support de caméra avec un troisième pied.

2. Eliminer les miroirs pivotants

Nous avons remplacer les miroirs pivotants par des cubes séparateurs (voir Figure 14). Ainsi, pour changer d?axe de mesure nous n?avons qu?à déplacer deux obturateurs, ce qui ne modifie en rien les réglages du montage.

2. Le logiciel FA95

Fringe Analysis 95 est le logiciel d?acquisition et de traitement des images développé par Holo3. Ses différentes fonctions nous ont permis d?exploiter facilement nos mesures (les fonctions décrites ci-dessous sont celles que nous avons le plus utilisé).

1. L?acquisition et la visualisation

FA95 fait des saisies d?images de la rondelle via la camera CCD et la carte d?acquisition Matrox. Ces images son stockées sous forme de fichiers bitmap [.bmp]. L?affichage peut se faire de plusieurs manières : en noir et blanc (linéaire, logarithmique, exponentiel, ...) ou en fausses couleurs (pseudo - couleurs, sépia, arc-en-ciel, ?).

On peut avoir un affichage continu de ce que voit la caméra : le logiciel rafraîchit l?image dès qu?il reçoit des données. Une fonction très utile, est celle qui permet d?afficher les soustractions des images successives : elle nous montre en continu les différences entre deux acquisitions et donc nous permet d?observer toutes les vibrations du montage qui influent sur l?éclairement de la rondelle. C?est avec cette fonction que nous avons pu observer une réelle amélioration de la stabilité de notre montage après les modifications.

2. Recherche de tension

Pour pouvoir calculer la carte des phases, il faut chercher le décalage de tension pour laquelle on a un décalage de phase de 2P . De plus, il faut régler la tension minimale afin de se placer dans la zone la plus linéaire du miroir piézo-électrique.

La fonction " recherche de tension " fait varier linéairement la tension piézo entre deux seuil préalablement définis et affiche la courbe de l?intensité en fonction de la tension (voir Figure 6). Un exemple de courbe est donné Figure 17.

Il faut relever la tension seuil à partir de laquelle le piézo est linéaire. Il faut noter également l?intervalle de tension pour lequel on passe d?un maximum à un autre (ce qui correspond à un déphasage de 2P ). Le piézo est très sensible aux vibration, l?obtention d?une courbe lisse est signifie que le montage est suffisamment stable.



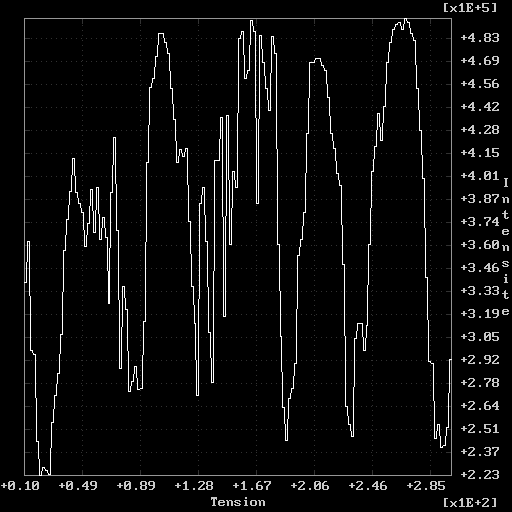
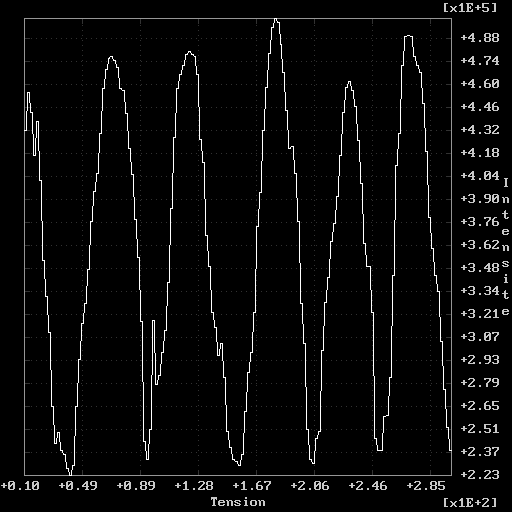
a) Courbe sans perturbation. b) Courbe avec perturbation.

Figure 17. Courbe de recherche de tension.

3. Les fonctions spécifique

En plus des fonctions très générales telles que les opérations ou les filtres, FA95 nous propose des fonctions plus spécifiques à l?analyse de déformations par TV - holographie.

1. Décalage de phase

C?est cette fonction qui calcule la carte des phases. Pour cela, il faut lui rentrer les tensions lues sur la courbe de recherche de tension.

2. Soustraction d?images phasées

La soustraction de deux cartes des phases permet d?obtenir les franges qui sont une première caractérisation des déplacements sur la rondelle.

3. Filtrage d?image phasée

Cette fonction rend les niveaux de gris directement proportionnels à la valeur de la différence de phase (voir Figure 18).



Figure 18. Filtrage d?image phasée.

4. Démodulation d?une image phasée

Après avoir indiqué l?origine des phases sur l?image, cette fonction ajuste toutes les valeurs de phase par rapport à cette origine en ajoutant une constante proportionnelle à l?ordre de la frange considérée.

On lui donne la longueur d?onde et l?angle d?éclairement et l?ordinateur calcul la carte des déplacements.

Pour que cette fonction marche, il est nécessaire d?avoir appliqué un filtrage d?image phasée sur l?image considérée.



Figure 19. Démodulation d?une image phasée.

4. Fonctions de mécanique

Le logiciel contient aussi quelques fonctions de calcul de RDM (Résistance Des Matériaux).

1. Les vecteurs de déplacement

Cette fonction combine les deux cartes de déplacement pour tracer une carte globale des déplacement dans le plan. La rondelle est échantillonnée et le programme affiche le vecteur de déplacement pour chacun de ces échantillons.



Figure 20. Vecteurs de déplacement.

2. Calcul des contraintes

Cette fonction reprend la formule 14 (paragraphe 2.4, page *), et les images obtenues après la démodulation. Après calculs, elle retourne des images des contraintes suivant X, suivant Y et suivant la diagonale.

3. Les mesures

1. La méthodologie

Voici les étapes proposées pour la mesure des déplacements, des déformations et des contraintes dans une pièce par holographie de speckle numérique.

(a) On centre dans un premier temps la rondelle dans l?étau, puis on applique une première contrainte à cette rondelle.

(b) On vérifie ensuite le réglage des faisceaux d?éclairement de l?échantillon (Il faut faire en sorte d?avoir un maximum d?intensité lumineuse sur la rondelle).

(c) On place le montage dans la configuration d?éclairement selon un axe X.

(d) On étalonne ensuite le système déphaseur (miroir piezo-électrique) grâce à la fonction " Recherche tension pour un déphasage de 2p " (Cliquez sur Frange puis Recherche tension). Cette fonction permet de repérer l?intervalle de tension qu?il faut appliquer au miroir piezo-électrique pour obtenir un déphasage de 2p .

(e) Puis on saisie la carte des phases en X à l?aide de la fonction " décalage de phase " (Cliquez sur Frange puis Décalage de phase). Cette fonction permet de calculer la phase en tous points d?une figure d?interférence grâce à la technique de décalage de phase (Figure 21).

Figure 21. Cartes des phases.

(f) On répète les opérations (c), (d) et (e) pour l?axe Y

(g) On applique à la rondelle une contrainte supplémentaire et on répète les opérations (c), (d), (e) et (f).

(h) On éclaire la rondelle fortement (en lumière blanche par exemple), on saisie l?image afin de créer un masque (Figure 22) à l?aide de la fonction " Binarisation " (Cliquez sur Image puis Binarisation)



Figure 22. Masque de la rondelle.

Une fois qu?on a obtenu les cartes de phase en X et en Y avant et après la déformation et le masque, Il ne reste plus qu?à traiter ces images par l?informatique.

(i) On soustrait les cartes de phase avant et après déformation, en X puis en Y, pour obtenir les images des franges d?interférence dans les deux dimensions.(Cliquez sur Frange puis sur Soustraction Image Phasée).

(j) On filtre ensuite les deux images obtenues grâce à la fonction " Filtrage image phasée " (cliquez sur Frange puis sur Filtrage Image Phasée).

(k) Les deux images filtrées doivent être ensuite démodulées grâce à la fonction " Démodulation de phase " (cliquez sur Frange puis Démodulation Image Phasée) Cette fonction réalise la démodulation d?image phasées codées modulo 2p et permet de quantifier l?information à partir des paramètres physiques du montage. On obtient alors les cartes des déplacements selon X et selon Y.

(l) On visualise maintenant les vecteurs déplacement dans le plan à partir des cartes des déplacements obtenues précédemment (Cliquez sur Mécanique puis sur Vecteur déplacement dans le plan).

(j) Pour terminer, on peut obtenir les déformations et les contraintes en chaque point de la rondelle à l?aide des fonctions " Calcul de déformations " et " Calcul de contraintes " du menu Mécanique.

2. Quelques résultats expérimentaux

Nous avons trois rondelles à notre disposition : une sans défaut, une avec un trou non débouchant et une avec un coup de scie à métaux le long du diamètre. Le trou non débouchant ne déformait les franges que très légèrement et seulement quand il était placé au plus près du mord mobile.

1. La rondelle sans défaut



Figure 25. Vecteurs de déplacement dans le plan.

2. La rondelle avec le coup de scie



Figure 29. Vecteurs de déplacement dans le plan, avec défaut.

3. Conclusion

Les modifications apportées au montage ont réellement facilité la prise de mesures et amélioré leur qualité. Nous sommes capables de mesurer des déplacements, des déformations et des contraintes appliqués à une pièce. Certains défauts sont visibles à condition qu?ils introduisent des discontinuités au niveau des déplacements. Les fissures sont des défauts idéaux, par contre, une bulle d?air ne déforment que très légèrement les franges, ce qui n?est pas suffisant pour pouvoir la localiser à coup sûr.

L?étau que nous avons utilisé a été modifier pour pouvoir y adapter une clé dynamométrique. Celle que nous utilisions n?était pas suffisamment précise pour apporter une réelle information sur la force appliquée. Le couple est gradué tous les 1 daN sur 20 daN, alors que les couples maximums que nous avons appliqué étaient de l?ordre de 2 daN. De plus, il faudrait avoir une idée de la variation d?espace entre les deux mords, ce qui permettrait de vérifier plus précisément les valeurs de déplacement obtenus.

Enfin, il serait intéressant de passer à des mesures de déformations en trois dimension en ajoutant au montage un système de mesure hors - plan. Ceci permettrait de mesurer des contraintes plus complexes et de pouvoir repérer plus facilement certain défauts.

4. Bibliographie