Overview: Introduction Battery-Resistor Model Comparison Goldman-Hodgkin-Katz Model Comparison Reuter-Stevens Model Comparison Conclusion

Introduction

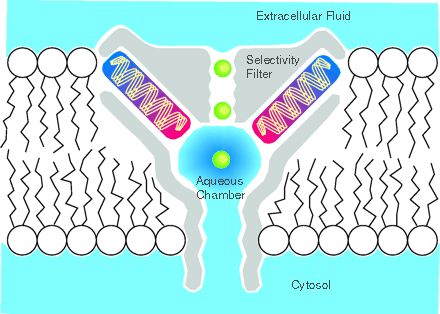
The potassium (kcsa) channel is a tetramer made up of four subunits. Each subunit contains an inner and outer alpha helix.  Together these four subunits give the channel a tepee structure, with the thinner side facing the intracellular matrix.  The inside of the potassium channel consists of two major regions that account for the channel's efficiency and selectivity, the inner pore and the selectivity filter.  The inner pore is lined with hydrophobic amino acids, which limit interactions with the hydrated ions in its cavity.  The selectivity filter is lined with main stem carbonyl oxygens which act as hydrophilic atoms.  Potassium ions are naturally hydrated with water molecules to balance its positive charge.  When potassium enters the inner pore, it remains hydrated because of the pore's relatively large entrance.  Many potassium ions can be found in the inner pore because of its large volume. However, when the ion reaches what would be the middle of the phospholipid bilayer, it becomes electronically unstable because of the high free energy in the center of the separated charge bilayer.  In order to aid the passing of the ion through this region, the structure of the channel is specialized in two ways.  First, the large cavity in the center allows the ion to be highly hydrated for some destablization.  Second, C-terminus of the inner alpha helices of the four subunits which are negatively charged are directly pointed to this region of destabilization to again balance the positive charge of the ion.  These two structural modifications allow the ion to pass without becoming unstable.

    The potassium ion must be dehydrated upon entering the selectivity filter because of it's narrow opening.  But of course, if the positively charged ion is dehydrated, it will be unstable.  To ompensate for dehydration, the inside of the selectivity filter is lined with carbonyl oxygens which are negatively charged.  This takes the place of the originally surrounding water molecules.  The potassium ion is postulated to have the same diameter as the selectivity filter.  This is so because then the potassium ion can be completely surrounded by the carbonyl oxygens to stabilize the charge.  On the other hand, a sodium ion is too small to enter because it would not be completely surrounded by the carbonyl oxygen to balance the energy gain from dehydration; hence the selectivity of the potassium channel.
 

Battery-Resistor (BR) Circuit Model

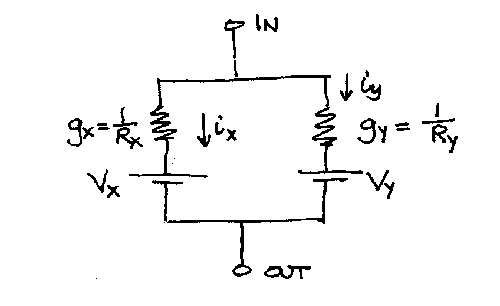
Goldman-Hodgkin-Katz (GHK) Circuit Model

This model is analgous to the Battry-Resistor model in the way the circuit is set up; the battery and resistor are connected in series for one ion passing through a hypothetical channel. However, there are some major differences between this model and the simple BR model. It is composed of parallel components of ions with different permeabilities (i.e. individual BR models of different ions are connected to each other in parallel).  The current equation agrees with the rectification effect discussed previously. For the reversal condition (I=0),

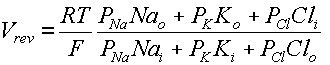
Where P denotes the permeability of the ion.

The assumptions for the validity of the model were:
                    1. An ion passing through the channel obeyed the Nernst-Planck Equation
                    2. Ions moving through the channel moved independently
                    3. A homogenous electric field existed within the channel
With respect with the model determined by crystallography, apparently none of these assumptions hold true. (1) Concentrated regions with different charges violate the validity of the Nernst-Planck equation applying to the entire channel. (2) Since the channel allows for only one ion to pass through due to a high selectivity, there needs no assumption that different ions move independent of each other. Even between potassium ions, the close proximity repulsive property is used to release the ion. Hence even the selected ion which passes through does not move independent of its own ions. (3) There also exists many complex energy barriers within the model, which violate the validity of the existence of a homogenous field within the channel. It is intiuitive that most of the energy associated with the channel lies in the selectivity filter.

    One primary disadvantage to this model is that the model is not a very physical model. It does not predict any complex structure within the channel. Even though the assumptions in the GHK model are invalid, the model closely predicts the macroscopic behavior of the channel. Hence, this model is widely used as an approximation in this field of research. Next, we discuss a model parallel to the GHK, which takes into consideration energy barriers which may be encountered by the travelling ion.
 

Reuter-Stevens Model

Slides:
1. Derivations
2. Small Delta Calculations
3. Barrier Calculation With A Potential Gradient

    The Reuter-Stevens model accounts for the physical nature of the channel by extending the GHK model by attributing the permeability with the rate of reaction by which the ion passes through the channel. Reaction denoting the different energy barriers with respect to binding within the channel (eg. to negatively charged lining of the selectivity filter). The model assumes one energy barrier, but it can be applied to a series of binding sites. This model can be applied to the real model if the barrier were approximated to be close to the selectivity filter. Then, it would correctly predict the unidirectional flow of ions, and the binding property of the filter. The mathematics involved in these calculations is left for the reader to investigate.

To verify Reuter-Stevens' single barrier model we see that it is very applicable to the physcial model. A major portion of the interior of the channel is water-filled. So, the polarized water can stabilize the ion when the ions cross the membrane. Therefore there is very little activation energy needed to be overcome. This cavity is strategically connected to the center of the membrane. The amount of energy required to reach the center of the membrane are reduced drastically. The four pore helices lay so that the electron-donating carbonyl groups are facing the pore opening, structurally avoiding energy wells near the center of the membrane while imposing  a negative electrostatic field, thereby so stabilizing the cation. The steps of stabilization that lower the overall energy required to move from inside of the membrane to outside is very small. Therefore, the selectivity filter is the rate limiting step, the step of greatest energy; hence, the single barrier in the reuter stevens model.
 

Applying the approximate single barrier assumption to the channel, the current obtained is:

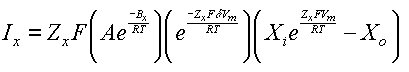
Where Bx denotes the energy required for the ion to pass through the barrier. Applying reversality (I=0):

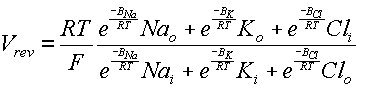
    This model can be applied for the series of energy barriers, which would make the Reuter-Stevens model a very good model to apply to the system. Since it is quite complex to take into consideration the energies of each of the barriers, the GHK equation is widely used as a general approximation of the model.
 

Conclusions

    Each of the 3 common models describing the behavior of the potassium channel have some insight into the behavior of the channel. However, the GHK model closely resembles the reality of the channel, without much complexity. It is quite remarkable to observe the intelligent design involved in a channel, which is much smaller than a single cell in our body!
 

References

D.A. Doyle, J.M. Cabral, R.A. Pfuetzner, A. Kuo, J.M. Gulbix, S.L. Cohen, B.T. Chait, R. MacKinnon, The structure of the potassium channel: molecular basis of K+ conduction and Selectivity, Science 280 (1998) 69-77.