HOOFDSTUK 5

Alfa-informatie als de basisbouwsteen van het semiotisch landschap

 

 

In het vorige hoofdstuk hebben we de stuurloze beweging van niet-geinformeerde entiteiten beschouwd. Deze beweging leidt steeds tot de grootst mogelijke verspreiding, die tevens de meest waarschijnlijke evolutieweg is. De enige "gewoonte" die we kunnen waarnemen, is eigenlijk dat er geen specifieke gewoontes zijn met betrekking tot de interacties. "Chaos" is het belangrijkste kenmerk.

We moeten stilaan ook de grote hoeveelheid symmetrie en orde die we als mens rondom ons waarnemen, gaan beschrijven. In dit en de volgende 2 hoofdstukken zullen we zien hoe in bepaalde situaties, de evolutiestroom kan leiden tot structuren die ver afstaan van de verspreiding die we in het vorig hoofdstuk hebben waargenomen.

In hoofdstuk 3 hebben we beschreven hoe bij het uitoefenen van een zekere stress op een systeem, dit systeem de stress zal proberen "dempen". De "weerstand tegen verandering" en het "egoïsme" van de verschillende componenten van het systeem leidt hierbij tot een gemeenschappelijk gedrag, dat leidt tot de realisatie van een maximale flux. We hebben dit toen als volgt gesteld : "Elke wijziging van toevoer van de stroom van M/E/I naar het systeem toe, wordt dus tegengewerkt door een tegenstrijdige flux van het systeem zelf. Op deze wijze streeft het systeem (onbewust) naar zelf-behoud, wat op zijn beurt leidt tot de toestand van quasi-evenwicht rond de attractor."
Dit coherente gedrag was niet waar te nemen in systemen die zich chaotisch (of volkomen incoherent) gedragen, zoals een gas.
We zullen nu echter het andere eind van het spectrum bekijken, waar systemen de gewoonte hebben om zich uiterst coherent gedragen.

Terug naar de index van dit hoofdstuk

1. DE WET VAN HOOKE, OF WAAROM DE APPEL NIET VALT

Beschouwen we als éénvoudig model een appel die aan een boom hangt.

Het antwoord op de eenvoudige vraag "waarom valt de appel niet", is niet zo evident en kan op verschillende manieren worden beantwoord.
In essentie peilt de vraag naar de samenhang van materie in structuren. Wanneer we terugkijken in de geschiedenis dan zien we dat het tot in de zeventiende eeuw heeft geduurd vooraleer hier een algemeen aanvaard antwoord op werd gegeven.

Figuur H5F1 : "Waarom valt de appel niet ?" is een vraag die in meerdere "lagen" kan worden beantwoord

 

De eer voor het inzicht in de problematiek moeten we toebedelen aan Robert Hooke (1635-1702).

Hooke realiseerde zich dat, als een materiaal of een bepaalde structuur een weerstand biedt tegen een zekere belasting, dit enkel kan gebeuren door met een gelijke en tegengestelde kracht terug te duwen. Als je lichaamsgewicht je voeten op de grond duwt, dan duwt de grond met een tegengestelde doch gelijke kracht terug op je voeten. De appel valt niet op de grond, omdat de takken een kracht uitoefenen, die tegengesteld is aan deze van de zwaartekracht. Dit principe zit ook ingebakken in Newton’s derde bewegingswet, die zegt dat actie en reactie aan elkaar gelijk zijn, doch tegengesteld in richting. Als deze voorwaarde niet vervuld is, of met andere woorden, als de krachten niet in evenwicht zijn, dan zal de structuur breken, of zal het geheel gaan bewegen. In ons voorbeeld zou de appel vallen, als de takken, of het steeltje van de appel niet sterk genoeg zijn.

Als we een sterke tak hebben, zal deze een kracht ontwikkelen, die de appel omhooghoudt. Als er twee appels aan de tak hangen, zal de tak een opwaartse kracht ontwikkelen die exact tweemaal zo groot is als het gewicht van één appel. Dit betekent dus dat de appel niet valt, omdat de tak een veerkracht ontwikkelt, die exact gelijk is aan het gewicht van de appel, doch tegengesteld in richting.

We kunnen de vraag "waarom valt de appel niet ?" dus herformuleren tot "waarom ontwikkelt de tak een welbepaalde veerkracht ?".
Hoe kan een "domme" materie zoals een tak, erin slagen om dergelijke reactieve krachten te ontwikkelen ?

Rond ongeveer 1676 zag Hooke duidelijk in dat
1) Elke vorm van vaste materie zijn vorm verandert, door zichzelf samen te trekken of door uit te rekken, wanneer er een mechanische kracht wordt uitgevoerd
2) Het is precies de vormverandering, die de materie toelaat een mechanische veerkracht te ontwikkelen.
Deze principes zijn ook bekend als "De wet van Hooke" over de veerkracht :
"De kracht van een veer is evenredig met de uitrekking van de veer".

Alle materialen en structuren vervormen, zij het in verschillende mate, wanneer ze worden belast. Dit inzicht is intussen uitgegroeid tot een afzonderlijke wetenschappelijke discipline, namelijk de studie van de "elasticiteit". Dit is de studie van de interacties tussen krachten en vervormingen in materialen en structuren.

Van vele materialen zijn deze vervormingen duidelijk zichtbaar : planten buigen zich om de impact van de wind te minimaliseren, en rubberen banden van een wagen passen zich continu aan volgens de vorm van het wegdek, en dempen zo de schokken die de passagier ondergaat op een oneffen wegdek. Dat alle materialen dergelijke vervormingen ondergaan, is niet steeds zichtbaar met het blote oog. Wanneer we bijvoorbeeld een berg beklimmen, vervormt het contactoppervlak van de berg zich lichtjes onder de druk van onze voeten, ook al zien we niet altijd onze voetafdrukken.

Hooke is in zijn redenering nog een stuk verder gegaan.

Hij zag in dat bij elke structuur die vervormt als gevolg van een belasting, het materiaal waaruit de structuur is gevormd, intern wordt uitgerokken of samengedrukt. Deze vervorming gaat door in alle delen van het materiaal, tot op een zeer fijne schaalgrootte. Nu weten we dat deze vervormingen inderdaad zijn terug te brengen tot vervormingen op moleculaire schaal.

Met andere woorden, wanneer we een veer uitrekken of in elkaar duwen, trekken alle atomen of molecules evenredig uit elkaar, of worden de atomen of molecules dichter bij elkaar geduwd.

We weten nu inderdaad dat de chemische bindingen die de atomen en molecules bij elkaar houden, zeer sterk zijn. Als een materiaal door een belasting in elkaar gedrukt wordt of uitgerokken, kan dit enkel als alle miljoenen of miljarden bindingen tussen de atomen van het materiaal tegelijkertijd een kleine vervorming ondergaan. Deze uitrekking of samendrukking wordt voorgesteld in onderstaande figuur. Het is alsof de bindingen tussen de atomen of molecules fungeren als kleine veertjes, die de stress van de externe belasting tegenwerken door uit te rekken of samen te komen.

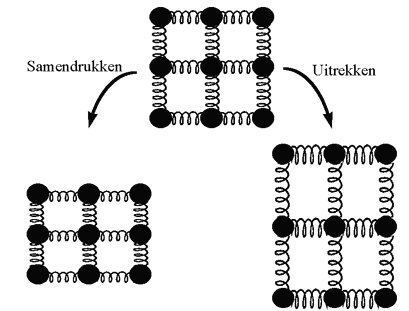
Figuur H5F3 : éénvoudig model van samendrukken of uitrekken van een materiaal (naar J.E. Gordon, 1978). Een materiaal in stressvrije toestand kan worden uitgerokken of samengeduwd. In het eerste geval wordt het materiaal langer, doordat de atomen zich van elkaar verwijderen, terwijl in het tweede geval de atomen dichter bij elkaar komen, en het materiaal korter wordt.

We kunnen nu stilaan de vertaalslag maken naar de terminologie die we voor "de gemiddelde evolutie" voorstelden.

De atomen en molecules zijn de interactoren binnen het materiaal. Wanneer we een bijkomende stress aan het materiaal opleggen, bijvoorbeeld een bijkomend gewicht aan een tak van een boom hangen, zullen elk van de atomen of molecules in de tak de stress trachten te dempen, door de positie tegenover de naburige interactoren te wijzigen. Doordat de miljarden molecules van de tak dit tegelijk doen, ontstaat een gezamelijke, zeer coherente beweging van de tak in zijn geheel. De microscopische dempingsbeweging van de individuele interactoren, heeft geleid tot een macroscopisch zichtbaar dempingspatroon van de tak in zijn geheel. Tijdens deze beweging is de coherente M/E/I-stroom of "flux" maximaal geworden. De verschillende interactoren hebben namelijk, vanuit hun "egoïstisch" karakter, de wrijving met hun directe buren trachten te beperken.

In tegenstelling tot een bij een gas, waar de verspreiding compleet is door de totale incoherente van de interactoren, is in dit geval de verspreiding nagenoeg te verwaarlozen, door de zeer hoge coherente van de interactoren. Daardoor wordt elke stress (of toevoer van M/E/I), snel en op zeer coherente wijze gedempt, door een tegengestelde beweging. Het dempingspatroon is hierbij zeer coherent, met andere woorden de flux wordt sterk gemaximaliseerd.

Maar waar zit dan de informatie die deze zeer coherente bewegingen aanstuurt ?

De hoge coherentie van de interactoren en hun interacties is terug te brengen naar een aantal zeer sterke attractoren. De "sterke kernkracht" en de "electromagnetische kracht" zijn de twee "universele" attractoren die de atomen en molecules samenhouden. Zij zorgen voor de bindingen tussen de molecules.
Deze elasticiteit van materialen is te wijten aan de universele Alfa-attractoren, die de bindingen tussen de materialen veroorzaken. Hieruit volgen op hun beurt de verschillende -voor veren kenmerkende- dempingspatronen en toestanden van quasi-evenwicht, die te beschouwen zijn als de attractoren van de contextuele interacties. Deze interactoren zijn -net als hun universele stamvaders- vormafhankelijke attractoren. Alle Alfa-attractoren zijn dus niet alleen vorm-afhankelijk, ze zijn ook duidelijk vorm-bepalend, omdat ze de vormen van de meeste materialen, al dan niet belast, bepalen.

Nadat aanvankelijk de flux (de coherente beweging van de tak) gemaximaliseerd werd, wordt geleidelijk aan deze flux gedempt, en komt de tak tot stiltstand. Een nieuwe toestand van "quasi-evenwicht" is bereikt, waarbij de macroscopische vorm van tak, in evenwicht is met de stress die erop wordt uitgeoefend. Dit evenwicht is maar een "quasi-evenwicht". Zodra we immers het gewicht opnieuw van de tak wegnemen, ontstaat opnieuw een zeer coherente fluxbeweging van de tak, totdat een nieuwe toestand van quasi-evenwicht is bereikt. Daar waar de zwakke en de sterke kernkracht universele attractoren zijn, die binnen de gemiddelde evolutie steeds opnieuw terugkeren, merken we dat elk van de interacties zelf, een toestand van quasi-evenwicht heeft met zijn eigen attractor.

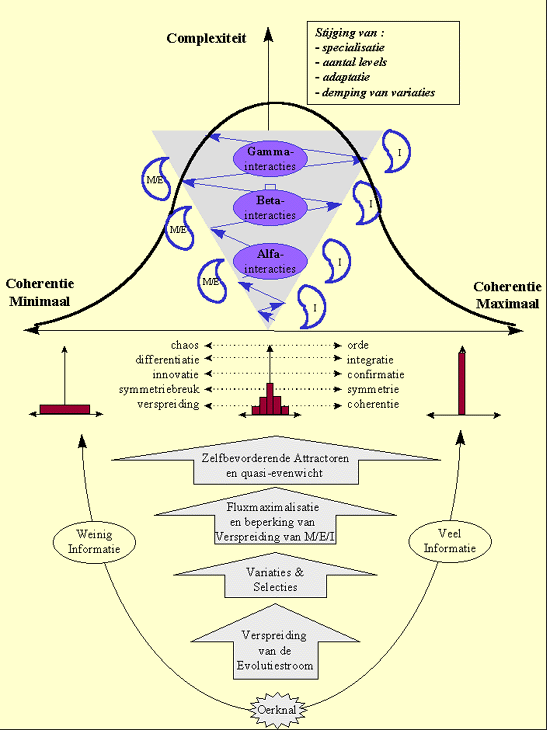
De attractoren van de gemiddelde evolutie, leiden dus tot talrijke nieuwe interacties, die hun eigen attractoren kunnen hebben, of met andere woorden, de interacties zelf hebben kenmerkende dempingspatronen, met kenmerkende toestanden van quasi-evenwicht. De gemiddelde evolutie heeft zijn kenmerkende Alfa-, Beta- en Gamma-attractoren, die op hun beurt leiden tot interacties met hun eigen attractoren en toestanden van quasi-evenwicht.
De "universele evoluationaire gewoontes" leiden op hun beurt tot nieuwe, al dan niet universele "gewoontes".

De evolutiestroom produceert zo steeds meer en steeds sneller nieuwe attractoren, die echter steeds minder universeel zijn, en unieker in hun voorkomen. Slechts enkele ervan zullen we steeds terugvinden in de gemiddelde evolutie, en kunnen we de Alfa-, Beta- en Gamma-attractoren van de gemiddelde evolutie noemen.

Het inzicht van Hooke is samen te vatten door te stellen dat alle materialen en structuren zich gedragen als een veer. Hooke publiceerde zijn inzichten in 1679 in een artikel genaamd :"De potentia restituvia" ( "over de veerkracht"), waarin het beroemde statement stond "ut tensio sic vis" (zo de uitrekking, zo de kracht").

2. DE GRAVITATIEWET VAN NEWTON, OF WAAROM DE APPEL WEL VALT

 

Isaac Newton (1647-1727) was een tijdgenoot van Robert Hooke, en ze kenden elkaars werk.

Hooke en Newton waren echter totaal verschillende persoonlijkheden, en zelfs persoonlijke vijanden.

 

Figuur H5f4 : Isaac Newton

In de 20 jaar dat Newton verderleefde na de dood van Hooke, heeft hij dan ook niet nagelaten zich minachtend uit te spreken over het werk van Hooke. Hooke zijn werk was praktisch gericht, waardoor het in die tijd minder aanzien genoot. Newton’s werk was meer theoretisch van aard, en zijn visie op het universum was ook breder dan die van Hooke. Daar waar Hooke bij zijn studie van materialen juist rekening hield met het type en de vorm, herleidde Newton de interacties tot abstracte evenementen tussen interactoren, waarvan het materiaaltype nauwelijks belangrijk was. Zijn gravitatiewet laat toe de interactoren tot hun zwaartepunt te reduceren, wat een extreem voorbeeld is van het negeren van de materiaaleigenschappen. Newton werd reeds als een held behandeld tijdens zijn leven, en door zijn sterke kritiek op het werk van Hooke, werd de studie van de elasticiteit van materialen voor meer dan 100 jaar terzijde gelegd. Nochtans zijn de basisprincipes van Hooke nu opnieuw in hun volle eer hersteld. Bij het ontwerpen van reusachtige flatgebouwen of moderne vliegtuigen, zal men bijvoorbeeld de elasticiteit van de gebruikte materialen en structuren afstemmen op de te verwachten stress (bijvoorbeeld door de wind).

Dat ze tijdgenoten zijn is echter onmiskenbaar terug te vinden in de basiswetten die ze hebben ontworpen.

Beiden hielden zich bezig met de "zeer coherente bewegingen", doch vanuit een verschillende invalshoek. Beiden hanteerden het basisprincipe "elke actie leidt tot een welbepaalde reactie, die gelijk is aan de actie, doch tegengesteld in richting". De abstractere wijze van denken die Newton hanteerde, is ook de basis geweest van zijn groter succes. Het heeft er immers toe geleid dat bepaalde zeer coherente bewegingen op een éénvoudige en kwantitatieve manier konden worden beschreven.

Daar waar Hooke’s wet van de veerkracht een goed inzicht geeft in de reden waarom een appel niet van een boom valt, geven de wetmatigheden van Newton juist een inzicht in waarom een appel wel zou vallen, en, als een appel valt, met welke snelheid hij dit zal doen. Laten we daarom eens de wetten van Newton doorlichten :

De eerste bewegingswet luidde als volgt : "Een object zal in toestand van rust blijven of in een rechte lijn blijven bewegen met constante snelheid, als het niet interageert met iets anders". Onze appel zal dus niet vallen, zolang we hem niet in beweging brengen. Om hem in beweging te brengen, moeten we een kracht uitoefenen. Een kracht werd door Newton gedefinieerd als iets dat de snelheid of bewegingsrichting van een object kan veranderen.
We hebben gezien dat Hooke had vastgesteld dat elk materiaal een weerstand uitoefent tegen vervorming. Newton stelde op analoge wijze vast, dat elk object een weerstand uitoefent tegen verplaatsing : deze weerstand tegen verplaatsing wordt de inertie van een object genoemd. (De weerstand tegen vervorming noemden we de "elasticiteit".) Wanneer we in een auto zitten, en de auto begint te bewegen, voelen we ons met de rug tegen de zetel gedrukt : dit is een uiting van de inertie van ons lichaam. Aangezien Newton zeer kwantitatief was ingesteld, wilde hij deze inertie ook meten : de maat voor de inertie noemde Newton "de massa". Hoe meer materie we hebben, hoe meer weerstand tegen verplaatsing we zullen hebben, en dus hoe meer massa.
We weten nu dus dat, als we onze appel in beweging willen brengen, we een kracht zullen moeten uitoefenen. Deze kracht zal echter afhankelijk zijn van de weerstand die de appel uitoefent tegen de beweging. Met andere woorden, we zullen moeten rekening houden met de massa van de appel. Met dit inzicht, heeft Newton zijn "tweede bewegingswet" opgesteld : "Wanneer we verschillende krachten uitoefenen op één welbepaalde massa, zal een grotere kracht, een grotere versnelling van het object tot gevolg hebben ; wanneer we eenzelfde kracht uitoefenen op verschillende massa’s, zal de versnelling kleiner zijn, naarmate de massa groter is." Newton wist dit elegant samen te vatten in de formule :
a = F/m (met a = de versnelling, F = de kracht, m = de massa).

Deze wetmatigheid is op zich heel krachtig. Het laat ons bijvoorbeeld toe te berekenen welke kracht we moeten uitoefenen met een tennisraket, om een tennisbal (van 60 gram) met een snelheid van 30 meter per seconde (ongeveer 110 km per uur) te laten bewegen. Als de bal aanvankelijk een snelheid heeft van 0 m/s, en de typische contacttijd van de raket met de tennisbal is ongeveer 0.005 seconde, dan is de vereiste versnelling :

a = (30m/s - 0 m/s) / 0.005 s = 6000 m /s²

Omdat de massa van de bal 60 gram is (0.06 kg), moeten we op de raket een kracht uitoefenen van

F = m.a = (0.06 kg) . (6000 m /s²) = 360 Newton.

We moeten dus een kracht uitoefenen die overeenkomt met een gewicht van ongeveer 36 kilogram (dit is niet zoveel, gezien de korte contacttijd).

Wanneer we op een tennisbal slaan, voelen we dat er tijdens het contact met de bal, een tegenkracht wordt uitgeoefend op ons lichaam.

Een gelijkaardige constatatie, leidde Newton tot het inzicht van zijn "derde bewegingswet" : "Wanneer een object een kracht uitoefent op een tweede object, dan oefent het tweede object een gelijke kracht uit op de eerste, doch tegengestelde in richting."

Met deze bewegingswetten, zijn we beter gewapend om de val van de appel te bekijken.
Als we een appel zien vallen, weten we dus dat er een kracht moet zijn die deze appel in beweging brengt. Newton zag in dat de kracht die werkt op de appel, dezelfde is als diegene die ons op de aarde vasthoudt, en ook dezelfde als diegene die de aarde rond de zon laat bewegen, of de maan rond de aarde : de gravitatiekracht.
Opnieuw slaagde hij erin zijn treffende observatie om te zetten in een elegante wet, "de gravitatiewet" : elk object in het universum trekt elk ander object aan, met een kracht die evenredig is met hun massa’s, en omgekeerd evenredig met de afstand tussen de objecten."

We weten nu dat de appel naar de aarde valt, omdat de zwaartekracht van de aarde de appel naar zich toetrekt. We zullen dit eens kwantitatief berekenen, om de kracht van de mathematische formules aan te tonen.

In een mathematische vergelijking, stelt de gravitatiewet dat de kracht F, die tussen twee objecten met massa’s m₁ en m₂ ageert gelijk is aan :

F = G * m₁ * m₂
R²

R is hierbij de afstand tussen de twee objecten en G is een natuurlijke constante, die dezelfde is op om het even welke plaats in het universum (de waarde van G is 6.670*10^-11 N*m²/kg²). Het punt vanwaar de afstand R moet gemeten worden is het zwaartepunt van het object.

Het feit dat R² in de noemer staat, wijst erop dat de gravitatiekracht heel snel daalt bij toenemende R.

Laten we dit nu eens toepassen op een vallende appel.

Wat gebeurt er met een appel als deze uit een boom valt ?

Experimenten geven ons hier het antwoord. Hoe hoger de plaats van waaruit de appel valt, hoe hoger de snelheid waarmee de appel tegen de aarde zal botsen. Deze versnelling is veroorzaakt door de aantrekkingskracht (gravitatiekracht) van de aarde.

Als de lucht geen weerstand zou bieden bij het vallen, zou elk object dat op de aarde valt, dezelfde versnelling van 9.8 m/s² hebben. Deze versnelling wordt gewoonlijk afgekort met "g".

Het gewicht van de appel stemt overeen met de gravitatiekracht die de aarde erop uitoefent :

- Gewicht van de appel = F₂ = m₂*g

De massa is een meer universele eenheid dan het gewicht, omdat het gewicht enkel relevant is voor de aantrekking door de aarde. "g" is de versnelling uitgeoefend door de zwaartekracht op een massa : deze is gelijk aan 9.8 m/s². De essentie van een kracht is immers dat ze een snelheid of de richting van de beweging van een object beinvloedt.
De wet van Newton laat ons dus toe de versnelling van de appel te kennen, alsook de aantrekkingskracht van de aarde tot de appel.

Aangezien F₂ gelijk moet zijn aan de gravitatiekracht F, kunnen we dus stellen dat F₂ = F₁, waaruit we de massa van de aarde kunnen vinden (m₁).

m₁*g = G * m₁ * m₂
R²

Hieruit vinden we dat de massa van de aarde gelijk is aan 6 * 10²⁴ kg : een enorm groot getal, doch de aarde is een relatief kleine planeet. Saturnus weegt 95 keer zo zwaar, en Jupiter ongeveer 320 keer zo zwaar. De massa van de zon is 300000 keer zo zwaar als die van de aarde.
De weerstand tegen verplaatsing van de aarde is dus zeer veel groter dan die van de appel, waardoor de appel naar de aarde valt en niet omgekeerd...

 

3. NEWTON EN HOOKE : GELIJKENISSEN EN VERSCHILPUNTEN

Kenmerkend voor de hoogcoherente systemen, zoals de appel die valt onder invloed van de zwaartekracht, of de de appel die niet valt, door de veerkracht van de tak van de boom, is dat de energiestroom op een zeer coherente manier verloopt.

In het geval van de buiging van de tak, zorgt de weerstand tegen verplaatsing van de miljarden molecules voor een coherente buiging van de tak. In het geval van de val van de appel, zorgt de weerstand tegen verplaatsing van de miljarden molecules van de appel, voor een coherente val van de appel. In het eerste geval wordt de samenhang tussen het ontelbaar aantal molecules ge-informeerd door de Alfa-informatie van de sterke kernkracht en de electromagnetische kracht. Deze beide Alfa-attractoren zorgen ervoor dat de molecules bij elkaar blijven, ook al staan ze onder een externe druk. In het laatste geval zijn de miljarden molecules in de appel geïnformeerd door de gravitatiekracht, die over langere afstanden heen, door het uitwisselen van zijn "boodschapperdeeltjes" (de gravitonen) - voor een coherente flux zorgt.

De informatieuitwisseling van deze attractoren is extreem coherent, en dus is ook de eruit voortvloeiende flux extreem coherent. Zodanig coherent dat er nauwelijks energie verloren gaat onder de vorm van verspreiding.

De microscopische weerstand tegen enerzijds vervorming en anderzijds verplaatsing, zorgt voor een macroscopisch zeer coherente flux.

Vandaar dat bij kwantatieve benaderingen van dergelijke hoog coherente bewegingen, de verspreiding zelfs volledig verwaarloosd is. (De fout die hierbij gemaakt wordt is verwaarloosbaar klein). In het geval van de chaotische beweging van het gas, konden we de coherentie verwaarlozen, omdat er nauwelijks of geen informatie aanwezig was, en in deze gevallen is de mate van geïnformeerdheid zo hoog, dat we de verspreiding kunnen verwaarlozen. Daarom hebben we gesteld dat dit twee uitersten van het spectum zijn. In volgende hoofdstukken zullen we de gevallen met een intermediaire coherentie bekijken : deze hebben een duidelijk hogere complexiteit.

De coherente stromen van energie kunnen arbeid verrichten, in tegenstelling tot de incoherente stromen van een gas. (Het coherente deel van de energiestromen wordt ook soms de exergie genoemd).

Dit belangrijke principe wordt in onderstaand schema en figuur uitgedrukt.

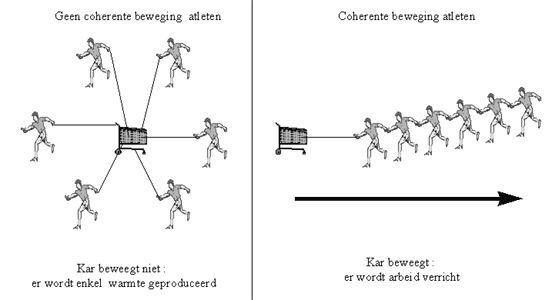
Stel dat we bijvoorbeeld 6 atleten een kar laten voorttrekken.

Indien we de atleten niet instrueren hoe ze de kar moeten trekken, zullen ze aan alle kanten van de kar trekken. Door deze niet-coherente beweging zal er geen arbeid worden verricht, doch zullen de inspanningen van de atleten "verspreid" worden onder de vorm van warmte.

Indien de atleten geinstrueerd worden om "aan hetzelfde eind" te trekken, zal de kar een coherente beweging vertonen. De energie van de atleten zal ook worden verspreid in warmte, doch in mindere mate, waardoor de kar vooruit zal bewegen.

Figuur H5F5 : coherente en incoherente bewegingen

Onderstaand schema vat dit proces als algemeen principe samen.

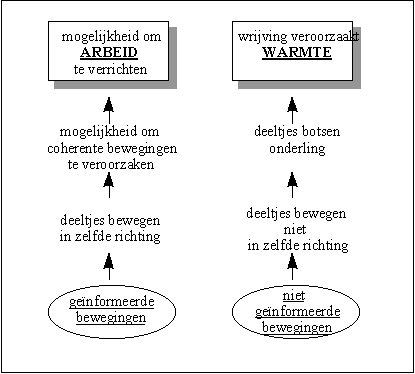
Belangrijke conclusie hierbij is de volgende :

De mogelijkheid om arbeid te verrichten, is het gevolg van de aanwezigheid van een geïnformeerde (coherente) beweging van de deeltjes (interactoren).

Indien de deeltjes op een niet-geïnformeerde wijze bewegen, kan enkel warmte worden geproduceerd.

Figuur H5F6 : het onderscheid tussen arbeid en warmte is terug te brengen tot een verschil in coherentie van de energiestroom

 

In de volgende paragrafen zullen we volgend principe verduidelijken :

Een coherente, geïnformeerde beweging enkel kan onstaan, als er attractoren aanwezig zijn.

De hoeveelheid arbeid die kan verricht worden door Alfa-geïnformeerde energiestromen, kan kwantitatief worden berekend :
"De arbeid verricht door een kracht op een object, is evenredig met de grootte van de kracht, vermenigvuldigd met de afstand waarover de kracht werkt".
Of : W = F . d (W = Arbeid, F = kracht, d = afstand waarover de kracht werkt).

In deze éénvoudige ( en zeer coherente) gevallen van de Alfa-attractoren, is de flux die maximaal kan worden ontwikkeld, gelijk aan de arbeid, die op de traditionele wijze wordt berekend.

Bij de complexe gevallen van stromen van materie, energie en informatie die minder coherent zijn, is deze éénduidige relatie tussen flux en arbeid niet meer te leggen.

Om de directe relatie te kunnen leggen tussen arbeid en flux, dienen twee belangijke voorwaarden voldaan zijn
1) De "Actie" moet zeer coherent zijn : dit is het geval indien er een universele Alfa-attractor aan de basis ligt van de actie.

2) De "Re-actie" moet zeer coherent zijn : de interactor moet perfect elastisch zijn.

Dat ook deze laatste voorwaarde niet steeds voldaan is, zullen we in de volgende paragraaf zien.

4. INELASTISCHE MATERIALEN EN NIET COHERENTE REACTIES

In de paragrafen over het werk van Hooke en Newton zijn we uitgegaan van de éénvoudige veronderstelling dat
- de actie die de "stress" veroorzaakt zeer coherent is (een Alfa-attractor)
- de reactie zeer coherent is.

Dit laatste veronderstelt dat de materialen van de interactoren perfect elastisch zijn.

Enkel voor perfect elastische materialen is er geen verlies van energie bij het samendrukken of uitrekken.

We zullen daarom eerst stilstaan bij minder ideale materialen, en bekijken hoe de "weerstand tegen vervorming" en "weerstand tegen verplaatsing" hier hun rol vervullen.
Daarna zullen we dieper ingaan op minder coherente acties.

 

4.1. Niet perfect elastische materialen

Laten we voor het bekijken de effecten van een niet perfecte elasticiteit eens terugkeren naar het voorbeeld van de vallende appel.
Gedurende de val van de appel, zal een maximale flux worden gerealiseerd. Wanneer de appel echter de aarde raakt, zal hij - door de botsing met de grond - wellicht opnieuw omhoog woren geduwd in de omgekeerde richting. De appel zal omhoog bewegen, tot de aantrekkingskracht van de aarde, gelijk wordt aan de opwaartse bewegingsenergie van de appel. Daarna zal de appel opnieuw naar beneden vallen. Deze beweging kan zich enkele malen herhalen, totdat de appel volledig tot stilstand komt.

De appel ligt dan bewegingsloos op de grond, en de macroscopische flux is stilgevallen. De appel heeft een nieuwe toestand van quasi-evenwicht bereikt.

In klassieke termen zegt men :
- aanvankelijk, toen de appel nog aan de tak hing, had deze een maximale potentiële energie ;
- deze potentiële energie is tijdens de val omgezet in kinetische energie (bewegingsenergie) ; alle potentiële energie die kon omgezet worden in bewegingsenergie, is ook omgezet : met andere woorden : de maximale flux is gerealiseerd, binnen de gegeven context ;
- bij de stilstand heeft de appel een toestand van minimale potentiële energie bereikt : alle potentiële energie die kon omgezet worden in bewegingsenergie, is ook omgezet en de flux is tot nul herleid.

We moeten ons nu echter afvragen waarom de appel tot stilstand komt op de grond. We zijn zodaning vertrouwd met deze gang van zaken, dat we dit "normaal" vinden.

Indien zowel de appel als de grond perfect elastisch zouden zijn (en de wrijving met de lucht te verwaarlozen zou zijn), zou de appel bij zijn opwaartse beweging opnieuw tot aan de tak moeten botsen, en daarna opnieuw naar de grond vallen, dan opnieuw tot op het niveau van de tak omhoog gaan, enzoverder. Dit neervallen en weer omhoog bewegen zou oneindig lang moeten voortduren (een perpetuum mobile), in tegenstelling tot wat we in de praktijk waarnemen. Om te begrijpen waarom de beweging van de appel stilvalt, zullen we terug moeten grijpen naar de overal voorkomende tendens naar verspreiding van de evolutiestroom.

Zoals we hierboven hebben beschreven, wordt de verspreiding tijdens de val van de appel beperkt door de aantrekking onder invloed van de gravitatiekracht. Nochtans is er ook bij de val van de appel een aanzienlijke verspreiding van materie, energie en informatie.

Het is precies de verspreiding van materie, energie en informatie die ervoor verantwoordelijk is dat de appel niet tot zijn oorspronkelijke hoogte naar boven komt na zijn botsing met de aarde, en dat hij na elke botsing minder hoog springt.

Om dit in te zien moeten we de appel opnieuw gaan beschouwen als een grote verzameling deeltjes (atomen, molecules,...) die gezamelijk een coherente beweging maken. Tijdens de val hebben al deze deeltjes een kinetische energie (of bewegingsenergie), die bij aanraking met de grond volledig omgezet wordt in potentiële energie. Op dit moment verandert dit ontelbaar groot aantal deeltjes gezamelijk van richting. Bij deze frontale en massale botsing met de aarde, gaan de deeltjes in de appel onderling botsen : de atomen en molecules raken elkaar langs verschillende kanten. Als gevolg hiervan gebeurt het veranderen van richting na de botsing zodanig, dat de massale hoeveelheid deeltjes overwegend opwaarts gaat bewegen. Doordat er bij de botsing echter ook vele willekeurige botsingen tussen de deeltjes onderling zijn gebeurd, wordt de potentiële energie niet volledig overgedragen in bewegingsenergie naar boven toe. Hierdoor zal de appel slechts weer beperkt in hoogte stijgen. Dit proces herhaalt zich totdat de appel volledig tot stilstand komt.

Indien de appel en de grond perfect elastisch zouden zijn, zouden bij de aanraking met de grond, de miljarden atomen en molecules in de appel tegelijk van richting moeten veranderen. De meest waarschijnlijke gebeurtenis is echter dat vele molecules willekeuring zullen bewegen, waardoor de appel niet tot zijn oorspronkelijke hoogte omhoog beweegt.

We zien dus dat aanvankelijk alle deeltjes in de appel een zeer coherente beweging maakten, onder "instructie" van de Alfa-informatie van de gravitatiekracht. Vooral bij het neerkomen van de appel wordt zowel de energie als de informatie verspreid, zowel binnen de appel, als in de atomen, molecules, kristallen en grassprieten van de grond. Door de onderlinge botsingen wordt de samenhang van informatie en energie verspreid : dit komt tot uiting door de vorming van warmte in de appel en in de grond die door de appel is geraakt.

Door de verspreiding wordt een coherente beweging (flux) van deeljes omgezet in een incoherente beweging.

Of nog anders uitgedrukt : door de verspreiding wordt een geïnformeerde beweging omgezet in een niet geinformeerde beweging.

Of in meer klassieke bewoordingen : door de verspreiding wordt arbeid wordt omgezet in warmte.

In de praktijk is geen enkel materiaal perfect elastisch, en zal bij de reactie steeds een deel van de stress worden omgezet in microscopische verspreiding, wat resulteert in het genereren van warmte. De voorwaarde voor "perfecte elasticiteit" komt overeen met de stelling "bij stress onstaat er geen microscopische verspreiding, doch wordt de stress volledig omgezet in flux". Als we een veer een lange tijd uitrekken en induwen, zal deze warm worden door de microscopische verspreiding. Slechts een deel van de stress wordt omgezet in flux.

De maximale flux die kan worden gerealiseerd (of de - in dit geval - maximale bewegingsenergie die kan worden ontwikkeld), zal afhangen van het type materiaal.

Indien we een bepaald type materiaal willen uitrekken, zullen we afhankelijk van het materiaal meer of minder stress moeten uitoefenen. De stress waarbij de lengte van het materiaal verdubbelt, wordt de "elasticiteitsmodulus van Young" genoemd. Thomas Young (1773-1829) ontwikkelde met zijn elasticiteitsmodulus een maat voor de veerkracht van elk materiaal.

 

 

Materiaal	Young’s modulus "E" (in MegaNewton/m2)
Rubber	7
Membraan rond eiwit van ei	8
Menselijke pees	600
Niet versterkte plastics	1400
Hout	14000
Beenderen	21000
Glas	70000
Aluminium legering	70000
Brons	120000
Ijzer en staal	210000
Diamant	1200000

Tabel H1T1 : de elasticiteitsmodulus van verschillende materialen (naar Gordon, 1978)

Naarmate de elasticiteitsmodulus groter wordt, wordt het steeds moeilijker om het materiaal uit te rekken. Rubber is heel veel makkelijker uit te rekken dan bijvoorbeeld diamant.
Wanneer een (volle) rubberen bal (van 1 kg) valt op bijvoorbeeld een stalen oppervlak, zal deze minder hoog botsen dan een diamanten bal. In de diamanten bal is veel minder microscopische verspreiding, waardoor deze bal hoger zal komen dan de rubberen bal na botsing op de bodem. Door de hogere coherentie van het materiaal in de diamant, wordt de stress van de botsing veel beter omgezet in een coherente flux, dan bij de rubberen bal. Dit is in belangrijke mate terug te brengen tot de symmetrie van het materiaal. Op moleculair vlak is diamant een heel symmetrische structuur, in tegenstelling tot rubber. (Merk in dit kader ook op dat in het begin van hoofdstuk 3, figuur 2, de diamant gesitueerd werd als een uiterst coherent object, met een relatief lage complexiteit).

In levende wezens is de elasticiteit van de componenten goed aangepast aan de functie. Onze slagaderen vertonen een lage elasticiteit, waardoor het hart bij het rondpompen van het bloed niet teveel wordt tegengewerkt. Deze aangepaste elasticiteit is noodzakelijk en belangrijk. Wanneer de mens ouder wordt, stijgt de elasticiteitsmodulus van de aderen, waardoor ook de bloeddruk stijgt en het hart een relatief zwaardere inspanning moet leveren. Vele mensen weten dit, doch weinigen denken eraan dat dit -mechanisch gezien - een gevolg is van de gewijzigde elasticiteit van de aderen.

De elasticiteit van de diverse materialen in ons lichaam is verbazend goed afgestemd op de functie die het moet uitoefenen. Op deze manier kunnen stresserende variaties in en op ons lichaam, optimaal worden gedempt.

De elasticiteit van bomen en planten is bijvoorbeeld ook een optimaal comprimis tussen de noodzaak aan het geven van voldoende stevigheid, zodat ze hun eigen gewicht kunnen dragen, en anderzijds voldoende flexibiliteit, zodat de structuren niet breken onder bijvoorbeeld een harde wind.

Ook bij het ontwerp van artefacten zal de mens rekening houden met de elasticiteit van de materialen, zodat structuur en functie maximaal op elkaar zijn afgestemd.

De vleugels van een vliegtuig zijn een gesofisticeerd compromis tussen sterkte en elasticiteit.

In een auto zullen materialen met een hoge elasticiteitsmodulus worden gekozen voor het geven van de stevigheid aan het onderstel en de carrosserie : dit moet een coherente (horizontale) voortbeweging mogelijk maken zonder al te veel "microscopische verspreiding" en warmtegeneratie. Nochtans worden er wel rubberen banden en zachte zetelkussens gebruikt, om de verticale variaties en oneffenheden in het wegdek niet op coherente wijze tot de passagiers te laten komen. Deze zachte materialen verspreiden de coherente schokken van het wegdek, tot incoherente en nauwelijks voelbare microscopische bewegingen van de zachte materialen : hierdoor wordt de stress op ons lichaam beperkt. Een perfecte schokdemper zou alle stress volledig omzetten in microscopische verspreiding. In de systeemdynamica wordt dit een perfect "dissipatief element" genoemd. Het woord "dissipatief" slaat net op de (microscopische) verspreiding die het element veroorzaakt.
Naarmate de complexiteit van de interactoren en artefacten in de evolutie stijgt, zien we een steeds gesofisticeerder gebruik van de verscheidenheid in dempingsgedrag van de verschillende beschikbare materialen. De flux wordt steeds subtieler, en wordt op steeds subtielere wijzen verspreid. We zullen in de volgende hoofdstukken dan ook "dissipatieve structuren" aantreffen, die veel complexer zijn dan een éénvoudige dissipatieve elementen.

 

 

 

4.2. Fasen, fasetransities en incoherente acties

We beseffen nu dat de verschillen in elasticiteit van materialen het dempingspatroon van externe mechanische stresscondities op min of meer coherente wijze zal dempen. De weerstand tegen vervorming verschilt sterk voor de verschillende materialen.

Tot nu toe beperkten we ons tot materialen in vaste toestand, maar hoe reageren vloeibare of gasvorminge interactoren op externe stress ?

Om hierop te antwoorden moeten we opnieuw de verschillen tussen gasvormige, vloeibare en vaste toestand eens op moleculaire schaal bekijken.

We zagen eerder dat bij een vaste stof, zoals ijs, de intermoleculaire krachten (Alfa-attractoren) heel sterk zijn. De krachten zijn zo sterk, dat de molecules niet vrij over elkaar heen kunnen bewegen. Het is alsof de molecules met veren aan elkaar zijn verbonden, en daardoor snel heen en weer vibreren.
Als we een gas vergelijken met een zwerm dolle bijen, die volledig onafhankelijk van elkaar bewegen, dan moeten we een vloeistof eerder vergelijken met het kruipen van bijen in een nest, waarbij de bijen kris-kras over en naast elkaar heen kruipen. Water tussen 0°C en 100°C vloeit, omdat de molecules langzaam naast elkaar heen glijden ; ze vloeien echter minder vlot dan in een gas (waterdamp), doordat er intermoleculaire krachten (Alfa-attractoren) de watermolecules over korte afstand bij elkaar houden. De molecules in een gas blijven echter niet bij elkaar omdat de intermoleculaire krachten niet voldoende sterk zijn.

Daar de verschillen in coherentie tussen een vloeistof, een gas en een vaste stof zo uitgesproken zijn, is het evident dat de reacties op een externe stress-factor ook duidelijk verschillend zullen zijn.

We hebben in de vorige paragrafen het voorbeeld gegeven van een slag met een tennisraket op een tennisbal. De tennisbal zal bij de slag eerst een fase van "microscopische verspreiding" doormaken, onmiddellijk na het contact met de tennisraket. In deze fase is er als het ware een strijd tussen de "weerstand tegen verplaatsing" van de bal (die gerelateerd is met zijn massa) en de kracht van de slag. Heel snel echter zal de kracht van de slag de inertie van de bal overwinnen, en zal het principe van de fluxmaximalisatie duidelijk worden. Hierbij zullen alle molecules in de bal een gezamelijke coherente beweging maken.

Indien we met een tennisraket op eenzelfde massa water zouden inslaan, zou de microscopische verspreiding de overhand houden. Van een coherente beweging van de watermassa zou geen sprake zijn, precies omdat de aantrekkingskracht tussen de watermolecules niet krachtig genoeg is om de watermolecules samen te houden. In dit geval is de actie wel coherent, doch is er niet echt een coherente reactie of een coherent dempingspatroon.
Indien we met een tennisraket op een volume waterdamp of nevel zouden slaan, is de coherentie wel helemaal zoek. We zullen bij de slag nauwelijks een weerstand ondervinden. In dit geval is de microscopische verspreiding maximaal, en is er totaal geen macroscopische flux.

Dit betekent echter niet dat vloeistoffen of gassen nooit coherente dempingspatronen kunnen ontwikkelen.
Reeds 2 millenia geleden ontdekte Archimedes dat een vloeistof een opwaartse kracht uitoefent. De wet van Archimedes zegt dat als we een appel in een kom met water zullen gooien, het water een weerstand tegen verplaatsing zal ontwikkelen die gelijk is aan het gewicht van de appel, doch tegengesteld in richting. Merk op dat het water zich in dit geval qua vorm perfect aanpast aan de opgelegde stress. In volgende hoofdstukken zullen we complexere dempingspatronen zien, die gekenmerkt zijn door complexere aanpassingen aan de opgelegde stress (inkomende stromen van M/E/I).
Zowel vissen als diepzeeduikers houden hiermee rekening. Ze regelen immers hun densiteit door opname en afgifte van lucht (bij duikers uit hun flessen), zodat ze naar wens kunnen stijgen, dalen of blijven zweven.
Ook gassen hebben - ondanks hun hoge incoherentie - bepaalde coherente dempingspatronen.

De wet van Boyle zegt dat, als we op een bepaald volume gas een bepaalde druk uitoefenen, het volume van het gas zal dalen, evenredig met de uitgeoefende druk. "Gemiddeld" gezien vertonen de gasmolecules dus een bepaalde aanpassing aan de opgelegde stress : ze zullen zich namelijk dichter bij elkaar bewegen.

Alle voorgaande voorbeelden zijn voorbeelden van min of meer coherente reacties op coherente acties.

We hebben aangetoond dat de coherentie van de reactie van materialen zeer sterk verschilt naar gelang de fase (vast, vloeibaar, gas) waarin het materiaal zich bevindt.

We zullen nu eens dieper ingaan op de fasetransities zelf, waarbij een gas verandert in een vloeistof, of een vloeistof in een vaste stof. Deze transities kunnen ook beschouwd worden als dempingspatronen, in dit geval echter als gevolg van incoherente acties. De incoherente actie die aan de basis ligt van deze transities is namelijk een wijziging van temperatuur, met andere woorden een wijziging van de gemiddelde bewegingsenergie van de molecules.
De overgang van vast naar vloeibaar, of van vloeibaar naar gas, kunnen beschouwd worden als aanpassingen aan variaties van de temperatuur.

• van vloeibaar naar gas en omgekeerd
  Wanneer we een vloeistof verwarmen (met andere woorden warmte toevoeren door de temperatuur te verhogen), zal de snelheid van de molecules in de vloeistof toenemen. Bij een bepaalde temperatuur, zal de gemiddelde snelheid van de molecules hoog genoeg zijn, om de intermoleculaire krachten te overwinnen, waardoor de molecules ontsnappen uit de vloeistof in de lucht. Het water begint te koken bij een kookpunt van 100°C.
  Om 1 kilogram water te verdampen, moeten we 2260kJ warmte toevoegen (dit is een toevoer van een incoherente energiestroom, beter gekend onder de naam "verdampingswarmte"). Aangezien de watermolecules in de waterdamp en in het water bij 100°C dezelfde kinetische energie hebben, kunnen we ons afvragen waar de 2260kJ naartoe gaat.
  Het antwoord vinden we bij de intermoleculaire krachten. We moeten de warmte-energie toevoeren om de watermolecules van elkaar te scheiden. Elke molecule moet, tegen de aantrekkingskracht van zijn naburige molecules in, weggetrokken worden, naar een afstand die ver genoeg is om de aantrekkingskracht niet meer te voelen.
  Net zoals we energie nodig hebben om een steen in de lucht te gooien, weg van de aantrekkingskracht van de aarde, moeten we hier energie toevoeren om de molecules vanuit elkaars aantrekkingsveld te laten ontsnappen.
  
  Bij omzetting van waterdamp in water gebeurt het omgekeerde. De molecules in de waterdamp worden door elkaar aangetrokken, en "vallen naar elkaar toe", waarbij de warmte-energie die vrijkomt wordt opgenomen door de omgeving.
• van vast naar vloeibaar en omgekeerd
  Vaste stoffen kunnen we in twee klassen indelen. Het grootste deel is "kristallijn", waarbij de molecules geordend zijn in zich herhalende drie-dimensionele patronen. Ijs, zout, kwarts, diamant en metalen zijn hiervan voorbeelden.
  Vaste stoffen waarbij de molecules niet regelmatig geordend zijn, noemen we "amorf" ("zonder vorm"). Voorbeelden hiervan zijn glas en plastics (de amorfie is ervoor verantwoordelijk dat vele types glas en plastics doorschijnend zijn).
  De overgang van vast naar vloeibaar, is op dezelfde wijze te omschrijven als de overgang van vloeibaar naar gas. Ijs bijvoorbeeld moet verwarmd worden om te smelten : de "smeltwarmte" is voor water 335kJ per kg. Deze energietoevoer is noodzakelijk om de molecules uit hun sterk geordende toestand te laten ontsnappen naar de minder geordende toestand in de vloeistof. Een overgang van een amorfe vorm naar een vloeibare vorm vereist doorgaans minder energie, omdat de molecules in de amorfe vorm relatief minder goed geordend zijn dan in de vaste vorm.
  
  Omgekeerd gebeurt het bij koelen van water onder 0°C, de spontane transitie naar ijs. Hierbij komt de "smeltwarmte" vrij aan de omgeving.

 

Beschrijving in termen van stroom van materie, energie en informatie :

• fasetransities : een gewoon proces ?
  Een fasetransitie is bij nader inzien op zijn minst een merkwaardig proces.
  Bekijken we bijvoorbeeld een voetbalstadion, waar voor de openingsceremonie van de Olympische spelen een groep dansers (tot honderd en meer) zich in formatie gaan bewegen. Hierbij kunnen ze bijvoorbeeld gezamelijk een stervorm aannemen. Voor de honderden miljoenen televisiekijkers is dit een bewijs van het menselijk vernuft, en van het menselijk ras dat zichzelf en zijn dierlijke aard steeds verder overtreft. De dansers slagen hierin omdat ze gedurende maanden getraind zijn om deze stervorm te vormen. Bij deze training hebben choreografen instructies gegeven over hoe de dansers elkaar moeten bekijken om "in de pas te lopen". Op de ultieme dag zullen ze hier dan ook wellicht feilloos in slagen.
  Van dit uitzonderlijke schouwspel naar een meer alledaagse vertoning nu : een vertoning die onze verbazing niet meer wekt : de vorming van een sneeuwvlok.
  Bij de vorming van een sneeuwvlok zullen op een bepaald moment niet honderd, maar miljarden keren miljarden molecules zich op een zeer korte periode groeperen in een stervormige formatie.
  Zonder training, zonder choreografen, zonder brein en zonder applaus.
  Hun vorm kan echter nog veel mooier zijn dat wat een groep menselijke dansers kan verwezenlijken, en bovendien kunnen er op korte tijd ontelbaar vele sneeuwvlokken tegelijk worden gevormd.
  In de onderstaande grafiek is een foto weergeven van een dergelijke sneeuwvlok.

Figuur H5F6 : zeshoekige structuur van een sneeuwvlok

• Waar halen de molecules in het ijs hun instructies vandaan ?
  Bij de groep dansers in de Olympische spelen is de sterke ordening te wijten aan de gedetailleerde instructies van de choreograaf. Deze instructies zijn tijdens de talrijke trainingssessies in het brein van de dansers geprent, waardoor ze bij hun finale optreden deze choreografie vrijwel foutloos kunnen repliceren.
  Als we de analogie met de molecules in het ijs willen doortrekken, moeten we ons afvragen waar deze molecules hun instructies vandaan halen.
  Hiervoor is maar één mogelijkheid : elke watermolecule moet de informatie om zich te groeperen in zich dragen. De informatie is dan ook de vorm van de molecule zelf : het is vormafhankelijke informatie of "Alfa-informatie". De attractor die hier aan de basis ligt is de universele electromagnetische kracht van de watermolecules, die de watermolecules naar elkaar toe aantrekt.
  Bij 0°C zal de snelheid van de watermolecules dalen beneden een kritische snelheid. De molecules krijgen betekenis voor elkaar en gedragen zich niet meer volledig onafhankelijk. Op een bepaald moment zullen op een bepaalde plaats bepaalde molecules stoppen met over elkaar heen glijden, en zullen ze zich naast elkaar leggen, op de wijze die het best past bij hun moleculaire vorm : dit is de vorming van een "kristalkern" of "nucleus". Na deze "nucleatie" zullen ook andere molecules zich hieraan hechten, steeds op vergelijkbare wijze. Het kristal groeit, tot het zichtbaar wordt voor het menselijk oog. De macroscopische vorm van het kristal weerspiegelt de vorm van de molecule. Eén watermolecule kan beschouwd worden als een driehoek. Twee molecules zullen samen een zeshoek vormen, die bij de kristalvorming teruggevonden wordt in de 6-hoekige vorm van het sneeuwkristal.
  De fasetransitie is voltooid.
  Omdat het een transitie is onder invloed van Alfa-informatie, noemen we dit in dit boek verder een Alfa-transitie.
• Symmetrie van het sneeuwkristal
  Een sneeuwkristal heeft een zeer mooie en symmetrische vorm, die terecht onze verbazing wekt. Er is duidelijk een zesvoudige rotatiesymmetrie waar te nemen, die de symmetrie van het zeshoekige moleculenpaar weerspiegelt.
  De macroscopische symmetrie van vloeibaar water is echter veel hoger. Hoe we een fles water ook draaien of keren, het uitzicht van het water blijft invariant ; met andere woorden, de symmetrie is heel hoog.
  Dit betekent dus dat de spontane Alfa-transitie (van water naar ijs) gepaard gaat met symmetriebreuk.
• Waarom is het kristal symmetrisch ?
  In tegenstelling tot de dansers bij de voorstelling op de Olympische spelen, kunnen we de molecules niet aanleren om verschillende kristalvormen aan te nemen. Dit komt omdat ze maar een heel beperkte hoeveelheid informatie kunnen opslaan, namelijk de vorm is de informatie. Doordat elke watermolecule dezelfde vorm heeft, bezit ze dezelfde informatie, en zal het patroon of de vorm van het entkristal, eindeloos worden herhaald totdat het macroscopisch zichtbaar wordt.
  De symmetrie van de natuur is een uiting van de beperktheid van de natuur.
  Symmetrie ontstaat omdat patronen worden herhaald.
  Patronen worden herhaald omdat de informatie van de interactoren beperkt is.
  Zoals het voor de dansers gemakkelijker is om steeds dezelfde figuren te dansen, is het voor de natuur gemakkelijker altijd dezelfde patronen te herhalen. De symmetrie in de natuur is dus eerder een uiting van de "luiheid" van de natuur, dan van de virtuositeit en de kunde van telkens te variëren.
• Symmetrie versus herhaling
  Aan de ene kant is er een continue tendens tot verspreiding van materie, energie en informatie. Deze leidt ertoe dat continu nieuwe vormen van materie, energie en informatie ontstaan.
  Aan de andere kant is de kunde van de natuur om te variëren ook beperkt. De natuur varieert niet eindeloos maar gebruikt "zijn beste ideeen" steeds opnieuw.
  De natuur heeft een tendens om gewoontes te vormen…
  Het gevolg van deze paradox is dat er in de grote diversiteit die we in de evolutie waarnemen, er ook een constante herhaling is van de basisbouwstenen. Deze herhaling in de tijd en in de ruimte is verantwoordelijk voor de macroscopische symmetrie en stabiliteit.

In de voorgaande paragrafen hebben we voornamelijk de Alfa-interacties besproken die gekenmerkt zijn door de wet van Hooke en de wetten van Newton.
We hebben aangetoond dat de wetmatigheden van Newton en Hooke van toepassing zijn op coherente interacties (acties en reacties) tussen coherente interactoren.
Indien de interacties perfect coherent zijn, kunnen we ook éénvoudige mathematische relaties opmaken, die de interacties met kwantitatieve precisie kunnen beschrijven. Zo kunnen we bijvoorbeeld de baan van de planeten rond de zon berekenen.
We hebben echter ook aangetoond dat lang niet alle materialen zo coherent zijn, en dat ook zeker niet alle acties coherent zijn. De eruit volgende reacties zijn dan ook in vele gevallen minder coherent, en vertonen een hogere complexiteit.

 

5. MEERVOUDIGE INTERACTIENIVEAU’S IN HET SEMIOTISCH LANDSCHAP

Naast de Alfa-attractoren die aan de basis liggen van de wetmatigheden zoals die door Hooke en Newton zijn geformuleerd, bestaan er ook nog verschillende andere universele Alfa-attractoren. De verschillende attractoren leiden dan ook op verschillende niveau’s tot kenmerkende interacties .

5.1. Evolutionaire successie van Alfa-attractoren

In hoofdstuk 3 hebben gezien dat de vorming van attractoren een spontaan en zelfversnellend proces is.
Eénmaal er attractoren gevormd zijn, is de kans groot dat van deze bestaande attractoren, nieuwe attractoren zullen afgeleid worden. Elke nieuwe attractor leidt hierbij tot specifieke interacties en interactoren, die nog niet bestonden op de onderliggende niveau’s. Er bestaat in de evolutie een bepaalde sequentie in de opeenvolging van deze attractoren : we zullen dit de "evolutionaire successie" van Alfa-attractoren noemen.

Zo kunnen we voor de universele Alfa-attractoren, een "stamboom" van interacties opmaken. Een voorbeeld hiervan is weergegeven in het onderstaande schema.

 

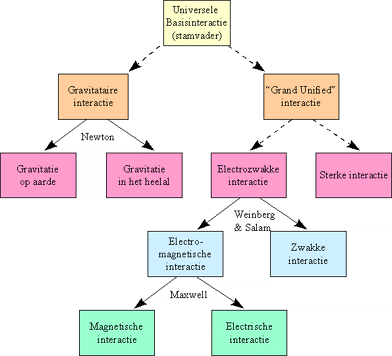
Figuur H5F7 : stamboom van de belangrijkste interacties als gevolg van universele Alfa-attractoren

Eén van de belangrijke doelstellingen van de fysica is precies deze stamboom van de interacties zo goed mogelijk te reconstrueren en te onderbouwen door wetmatigheden.

Voordat Newton zijn theorie wereldkundig heeft gemaakt, was het niet duidelijk dat het mechanisme dat "de appel naar de aarde doet vallen", hetzelfde is als datgene wat de planeten in hun orbitalen rond de zon doet draaien. Eén van Newtons grote verwezenlijkingen is precies aan te tonen dat dit twee fenomenen zijn van éénzelfde gravitaire attractie. De geniale vondst van James Maxwell (1831-1879) was dat alle magnetische interacties en electrische interacties, in feite terug te voeren zijn tot een gemeenschappelijke electromagnetische interactie. In de tweede helft van de twintigste eeuw slaagden Steven Weinberg en Abdus Salam erin aan te tonen dat de zwakke interactie en electromagnetische interacties ook terug te brengen zijn tot een gemeenschappelijke electrozwakke interactie.

De ultieme droom van de fysici is dan ook alle fysische interacties te kunnen terugbrengen tot één universele basisinteractie. In deze "Theorie van het alles" (Theory of everything) zou het bestaan van alle particels en alle interacties moeten verklaard worden.

In deze zoektocht naar deze fundamentele theorie van het alles, laten de fysici zich sterk leiden door de intuïtie dat de basiswetten van deze allesomvattende theorie een uiterst grote symmetrie bezitten. Deze intuïtie is gebaseerd op de vaststelling dat, gedurende de evolutie, de verschillende niveau’s gekenmerkt zijn door een toenemende symmetriebreking ; hieruit volgt dat de oorspronkelijke toestand uiterst symmetrisch en uiterst coherent moet zijn geweest. Ook de meest elementaire interactoren -zo redeneert men- moeten een uiterst hoge symmetrie hebben gehad. De reden waarom men deze meest elementaire interactoren de "supersnaren" noemt, heeft precies te maken met het feit dat ze supersymmetrisch zijn.
Door opeenvolgende symmetriebrekingen van de verschillende attractoren, ontstaan nieuwe niveau’s van interacties, die elk hun eigen afgeleide wetmatigheden en afgeleide attractoren hebben.

Elk niveau van attractoren, heeft zijn eigen vormen van informatie-uitwisseling. Op fysisch niveau, wordt deze informatie-uitwisseling bepaald door de uitwisseling van een boodschapperdeeltje. Het is de uitwisseling van dit boodschapperdeeltje tussen de objecten, die de attractie tussen de objecten veroorzaakt.

Fundamentele attractor	Boodschapperdeeltjes (van de attractor)
gravitatiekracht	gravitonen
zwakke kernkracht	W- en Z- bosonen
electromagnetische kracht	fotonen
sterke kernkracht	gluonen

Tabel H5T2 : universele Alfa-attractoren en hun respectievelijke boodschapperdeeltjes

Met uitzondering van het graviton, is het bestaan van deze boodschapperdeeltjes al experimenteel bevestigd. Indirect zijn er echter sterke aanwijzingen voor het bestaan van het graviton.

De uitwisseling van deze 4 types boodschapperdeeltjes, is verantwoordelijk voor de 4 basisinteracties die we in de fysica waarnemen.

Alle andere interacties zijn afgeleid van deze 4 universele krachten. Alle chemische krachten, die verantwoordelijk zijn voor de chemische bindingen tussen atomen en molecules, zijn afgeleid van de electromagnetische basiskracht. Het zijn de chemische krachten die de molecules in de appel chemisch aan elkaar binden, en bijvoorbeeld de dikke schil en het vruchtvlees vormen.

De appel op zich is een relatief stabiele toestand met een verhoogde waarschijnlijkheid, en kan daardoor ook een attractor worden genoemd. In tegenstelling tot de fundamentele attractoren in de fysica, is het echter geen universele attractor, doch eerder een relatief uitzonderlijke attractor, die tot stand gekomen is door een samenspel van zeer complexe informatie-uitwisselingen van Alfa-informatie, Beta-informatie en Gamma-informatie. De appel kunnen we wel een attractor noemen, doch geen attractor van de gemiddelde evolutie, omdat het onwaarschijnlijk is dat we de quasi-stabiele toestand die de appel kenmerkt, in de verschillende herhalingen van de evolutie zouden waarnemen.

We kunnen dit dus als volgt samenvatten :

Elk niveau van attractoren, is kenmerkt dus een niveau van dominante interacties, met een kenmerkend type van dominante informatie-uitwisseling.

Nieuwe types van informatie en informatie-uitwisseling, leiden elk op zich tot nieuwe niveau’s van attractoren, interactoren en informatie. Dit is precies de zelfversnellende cyclus van attractoren.

5.2. Niveau’s van articulatie in het semiotisch landschap

Een nieuw niveau van betekenisvorming, zullen we verder ook een nieuw niveau van "articalutie" noemen. Wanneer we over niveau’s spreken in de evolutie, zijn dit ook niveau’s van attractoren, interactoren en articulatie.

In de volgende hoofdstukken zullen we zien dat niet enkel voor Alfa-attractoren, doch ook voor Beta- en Alfa-attractoren meerdere niveau’s van articulatie bestaan. In onderstaande tabel wordt reeds een samenvatting gegeven van de niveau’s van articulatie die het belangrijkst zijn voor de evolutie.

Codering	voorbeelden articulatieniveau’s
Alfa	De diverse niveau’s van materie hebben elk hun eigen articulatieniveau : gravitaire interactie sterke interactie zwakke interactie electromagnetische interacie
Beta	De diverse niveau’s van stromingsprincipes vormen de verschillende niveau’s van articulatie : stroming in kanalen stroming in éénvoudige feedback-cycli stroming in hypercycli
Gamma	De twee bekende hoofdtypes Gamma codes : DNA code’s, met de dubbele articulatie codon’s-> genen menselijke taal, opnieuw met de dubbele articulatie : woorden -> zinnen

Tabel H5T3 : niveau’s van articalutie in de gemiddelde evolutie

Nieuwe niveau’s van articulatie vertonen een aantal types kenmerken.

• Ten eerste is er een toenemende onafhankelijkheid tussen de drager van de informatie, en de betekenis ervan. Bij de Gamma codes leidt dit zelfs tot een dubbele articulatie binnen één niveau, waardoor de complexiteit van de eruit volgende interacties en interactoren sterk toeneemt. De menselijke taal laat toe te communiceren met woorden, doch we kunnen ook woorden combineren tot zinnen. Met deze zinnen bezitten we over een vrijwel onbeperkt communicatie-arsenaal.
• Ten tweede is een toenemende mate van zelfbehoud. Door de toenemende complexiteit van de reacties, is de demping van de acties steeds gesofisticeerder en effectiever. Deze toenemende mate van zelfbehoud, is gekenmerkt door een toenemende mate van adaptatie van de systemen en hun reacties op de acties van de omgeving. Elk dempingspatroon is in feite een vorm van aanpassing aan de opgelegde stress (of variatie van M/E/I). We hebben aangetoont dat ook éénvoudige Alfa-interacties tot éénvoudige vorming van aanpassingen leiden.
• Ten derde is er een toenemende tijdsvertraging tussen actie en reactie. De dempende reacties die volgen op de stresserende acties, verlopen steeds trager, naarmate de interactoren een hoger interactieniveau bereiken. Naarmate we hogere niveau’s van interactie bereiken, verlopen niet enkel de reacties, doch ook de interacties steeds trager. Fotonen zijn de dragers van de electromagnetische kracht. Ze bewegen zich met een snelheid die we kennen als de snelheid van het licht. Dit is de maximale snelheid die bereikt kan worden. Menselijke communicatie verloopt bij verbale communicatie via geluidsgolven, die een heel stuk trager zijn dan electromagnetische golven. Bovendien meten de geluidsignalen nog vertaald worden in het lichaam van de ontvanger, waardoor de duur van de reactie heel wat toeneemt. Complexe levende systemen, zoals internationale bedrijven, re-ageren nog heel wat trager dan de individuen waaruit ze zijn samengesteld.

In de volgende hoofdstukken zullen hiervan nog verschillende voorbeelden gegeven worden.

Op elk niveau van articulatie heerst als het ware een eigen jargon, dat enkel door de interactoren op dat niveau wordt begrepen. De signalen hebben dus enkel betekenis op het betrokken niveau’s.

De klassieke visie op de natuur, is een visie die sterk gedomineerd wordt door de aard en de omvang van de stromen van materie en energie.
Naarmate we ons meer en meer bewust worden van de diverse types informatiestromen die er bestaan, zullen we de omgeving en het landschap rondom ons op een andere wijze gaan percipiëren.

Het landschap rondom ons bestaat heeft niet enkel materiële dimensies, die gekenmerkt wordt door materiële variaties van structuren in de ruimte zoals de huizen, bomen, bergen, kristallen, molecules, planeten en sterren.
Sinds de achttiende eeuw weten we dat we hier ook een energetische dimensie aan moeten toevoegen, er ook de talrijke stromen van energie, in al zijn verschijningsvormen, het landschap verrijken en boeiender maken.
Deze energetische dimensie benadrukt de dynamische variaties in de tijd.

Ons informatietijdperk maakt ons bewust dat deze energiestromen en materiële interactoren bestuurd worden door stromen van informatie. We moeten dus nog een informatie-dimensie toevoegen. De evolutie is niet enkel gekenmerkt door M/E stromen die wijzigen in tijd en ruimte, doch is ook onderhevig aan variaties in de betekenis die substromen van M/E/I voor elkaar hebben. Zonder deze informatiestromen, zouden er geen materiële structuren zijn, en geen coherente stromen van energie. Het landschap rondomons wordt meer en meer een landschap van signalen : het is een "semiotisch landschap". Dit semiotisch landschap bestaat uit 3 hoofdtypes informatie, namelijk Alfa-, Beta- en Gamma-informatie, met hun kenmerkende attractoren en interactoren, op elk van de diverse niveau’s en hun niches. Hierbij kunnen de Alfa-attractoren met hun Alfa-informatie als basisbouwstenen van het semiotisch landschap worden beschouwd.

In dit semiotisch landschap overleven in de evolutie deze stromen, die de informatie bevatten met de hoogste mate zelfbevordering, dus de hoogste graad van zelforganisatie en/of zelfbehoud. Deze zelfbevorderende stromen zijn de meest waarschijnlijke complexe stromen in onze gemiddelde evolutie.

Hoewel deze visie zeer eigentijds lijkt, en ingegeven door de sterke toename van het belang van informatie in ons dagelijks leven, is de essentie ervan reeds decennia geleden beschreven door de Duitse bioloog Jacob von Uexkull. Hij stelde reeds in 1940 dat de omgeving (in de context van de biologie) gedomineerd wordt door een uitwisseling van signalen.

6. CONCLUSIE

• De natuur vertoont een tendens om gewoontes te vormen.
  Hooke en Newton beschreven elk op hun manier enkele van de fundamentele evolutionaire gewoontes. Beiden gingen ervan uit dat de natuur een weerstand tegen verandering vertoont. Deze weerstand tegen verandering uit zich doordat elke actie, gevolgd wordt door een reactie. Deze reactie is in waarde gelijk aan de actie, doch tegengesteld in richting.
  Beiden slaagden erin kwantitatieve wetmatigheden te formuleren, om de interacties (de acties en reacties) te beschrijven. Deze wetmatigheden gelden voor zeer coherente acties, en zeer coherente materialen. De coherentie was te wijten aan de zeer coherente Alfa-informatie. In deze gevallen wordt de actie volledig tot een coherente stroom (flux) van M/E/I omgezet, en is de microscopische verspreiding minimaal.
  In realiteit zal noch de actie, noch de reactie een dergelijke "perfecte" flux realiseren. Bij niet-elastische materialen of incoherente acties, zal steeds een deel van de actie microcopisch worden gedempt, terwijl een ander deel - binnen de gegeven condities - een maximaal haalbare flux realiseert. De maximale flux wordt zal daarom niet steeds het niveau van de "perfecte flux" bereiken.
• In elk geval is de coherentie, zowel van de actie, als van de materialen, als van de reactie, te wijten aan de aanwezigheid van dominante informatie.
  We hebben gezien dat in de evolutie verschillende Alfa-attractoren elkaar opgevolgd hebben, en dat we een "stamboom" kunnen maken van deze vorm-afhankelijke evolutionaire gewoontes. Elk van deze Alfa-attractoren van de gemiddelde evolutie, kan tot vele andere attractoren leiden, die echter een minder universeel karakter hebben.
• Aan de basis van dit coherente gedrag ligt dus informatie.
  Deze informatie is het "programma" dat aan de basis ligt van de evolutionaire gewoontes, en beperkt zo de diversiteit van het evolutionair gedrag. Om die reden moeten we de natuur rondom ons niet enkel zien als een landschap van materiële structuren en energiestromen, doch ook als een landschap van signalen. In dit semiotisch landschap is de Alfa-informatie te beschouwen als de basisbouwsteen, die eerst is ontstaan in de evolutie. Later in de evolutie zijn de Beta- en Gamma-informatie ontstaan, die de complexiteit en diversiteit van het semiotisch landschap nog hebben verfijnd.
• Informatie kan dus spontaan ontstaan in het evolutionaire landschap, door het proces dat we flux-maximalisatie hebben genoemd.
  Van zodra informatie gevormd is, zal het leiden tot nieuwe types informatie : de natuur heeft dus niet alleen een tendens om gewoontes te vormen, ze doet dit ook steeds sneller en verfijnder…
  
  

 

HOOFDSTUK 5

Alfa-informatie als de basisbouwsteen van het semiotisch landschap

1. DE WET VAN HOOKE, OF WAAROM DE APPEL NIET VALT

2. DE GRAVITATIEWET VAN NEWTON, OF WAAROM DE APPEL WEL VALT

3. NEWTON EN HOOKE : GELIJKENISSEN EN VERSCHILPUNTEN

4. INELASTISCHE MATERIALEN EN NIET COHERENTE REACTIES

4.1. Niet perfect elastische materialen

4.2. Fasen, fasetransities en incoherente acties

5. MEERVOUDIGE INTERACTIENIVEAU’S IN HET SEMIOTISCH LANDSCHAP

5.1. Evolutionaire successie van Alfa-attractoren

5.2. Niveau’s van articulatie in het semiotisch landschap

6. CONCLUSIE