Tanto os antigos rituais como as mais antigas constituições maçônicas afirmam conjuntamente que a Maçonaria tem como finalidade o aperfeiçoamento do homem. Também os antigos Mistérios Clássicos tinham o mesmo objetivo e conferiam a "teletè" , ou seja, a perfeição iniciática. Esse termo técnico era, de acordo com o pitagórico Plutarco, etimologicamente associado a três significados: fim, morte e perfeição. Um manuscrito, achado pelo Locke [1] em 1696, enuncia expressamente a existência de uma relação entre a Maçonaria e a Escola Itálica fundada por Pitágoras mais de 25 séculos atrás. As mesmas Constituições de Anderson mencionam Pitágoras e o manuscrito de Cooke afirma ser a Maçonaria a parte principal da geometria. Fica, portanto, comprovado que a arte geométrica da Maçonaria deriva, direta ou indiretamente, da geometria e aritmética pitagórica.

Pitágoras (580-490 A.C.), discípulo dos mestres do Egito, da Grécia e da Caldéia, afirmava que a aritmética e a geometria não ficavam confinadas apenas no mundo da lógica. Muito pelo contrário, religião, moral, política, música, física, etc. unificavam-se no espírito cosmológico de uma autêntica teologia racional. Em particular, a geometria era a ciência que tinha por objeto o estudo do cosmo sob o aspecto da posição e da estensão. A aritmética era a ciência do ritmo, do número, do tempo, do intervalo, e o pitagórico Arquitas discriminava entre um tempo físico e um tempo psíquico.

Os números não eram considerados apenas em suas propriedades abstratas, mas também, e principalmente, em suas dimensões simbólica, psicológica, metapsíquica e esotérica. Portanto os números representavam as virtudes intrínsecas e efetivas do Grande Arquiteto do Universo, gerador e garantidor da ordem e da harmonia cósmica [2]. Para os adeptos da Escola Itálica o um, a unidade (mônade), não era um verdadeiro "número", mas o princípio gerador de todos os números. Analogamente o dois (díade) era tido como o gerador de todos os números pares. O primeiro verdadeiro número, o três (tríade), surgia da interação entre a mônade e a díade. Assim, todos os demais números podiam ser obtidos por simples adição a partir da unidade, criando assim uma progressão linear de números inteiros.

Todavia, a partir do três, os números podem também ter uma representação superficial. De fato o três pode ser imaginado como um terno de pontos dispostos nos vértices de um triângulo equilátero (número triangular). Assim, considerada a unidade como potencialmente triangular e o três como segundo número triangular, pode-se obter uma série ilimitada de sucessivos números triangulares mediante o desenvolvimento de um triângulo equilátero a partir de um de seus vértices. Aritmeticamente, escrita numa primeira linha a sucessão dos números lineares, pode-se deduzir a sucessão dos triangulares escrevendo a unidade sob a unidade e obtendo o triangular sucessivo como soma do elemento que o precede na mesma linha com aquele que o precede na mesma coluna:

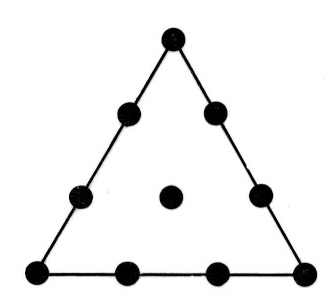
A partir do quatro os números admitem também uma representação espacial. Temos assim os números tetraédricos, piramidais, cúbicos, etc. É fácil observar como para delimitar um segmento de reta são necessários dois pontos, enquanto para delimitar uma porção de plano precisamos, no mínimo, de três pontos. Analogamente o número mínimo de planos ocorrentes para delimitar uma porção de espaço é quatro. O sólido formado pela intersessão de quatro planos é o tetraedro e, como nesse poliedro existem quatro vértices, apenas quatro pontos (tétrade) são necessários e suficientes para defini-lo univocamente. Segundo Platão o tetraedro é a última partícula que constitue os corpos: o átomo da natureza.

Em síntese, acrescentando uma unidade à unidade se passa do ponto à linha, delimitada por dois pontos; acrescentando a esses dois pontos um terceiro ponto se passa ao plano mediante o triângulo. Enfim, acrescentando mais uma unidade se passa ao espaço mediante o tetraedro e nessa altura o processo pára, pois não tem sentido acrescentar mais um ponto fora do tetraedro. O conjunto formado pela mônade, díade, tríade e tétrade compreende tudo: o ponto, a linha, a superfície e o espaço. De consequência, no pensamento filosófico pitagórico a "tetraktys" (grupo de quatro) dos números 1, 2, 3 e 4 é perfeita porque compreende todos os aspectos do universo material sólido. Sobre essa tetraktys os pitagóricos prestavam juramento com essas palavras:

"Eu juro por aquele que transmitiu à nossa alma a tetraktys, na qual se encontram a fonte e a raiz da eterna natureza".

Como a soma 1 + 2 + 3 + 4 = 10, também o 10 é um número perfeito. A perfeição, ou seja, o completamento da manifestação universal, é portanto alcançada com o número 10. A décade, que corresponde ao quarto número triangular, contém tudo, da mesma forma que a mônade contém potencialmente tudo. A representação geométrica do quarto número triangular é a seguinte:

Essa reprodução da tetraktys é um verdadeiro símbolo enquanto representa contemporaneamente um triângulo equilátero e dez pontos dispostos em quatro linhas contendo respectivamente a mônade, a díade, a tríade e a tétrade. A perfeição do 10 decorre também da observação que o homem possui 10 dedos e que o nosso sistema de numeração tem base decimal. Uma outra importante relação entre o dez e o quatro é que a quarta letra do alfabeto grego, Delta, é justamente a inicial da palavra grega decas (décade) e tem a forma de um triângulo equilátero. Sem dúvida, porém, a evidência mais impressionante do caráter globalmente simbólico da tectraktys decorre da relação entre o 4 e o 10 estabelecida pela física moderna. Efetivamente, embora o comportamento macroscópico do universo seja totalmente descrito por um sistema de referência espaço-temporal caracterizado por quatro dimensões (x, y, z, t) , as mais recentes teorias sobre a estrutura submicroscópica da matéria (superstring theories) necessitam de um espaço constituído de dez dimensões [3].

O símbolo pitagórico da tetraktys, na sua forma esquemática triangular, já existia no santuário de Delpho mais de 2500 anos atrás e coincide manifestamente com o Delta maçônico. Ocasionalmente o Delta tem sido interpretado como um símbolo da Trindade, mas o caráter esotérico do Delta pitagórico-maçônico nada tem a ver com o cristianismo, sendo a tetraktys um símbolo inegavelmente pagão.