LAZER DOKU ETKİLEŞİMİ İÇİN BİR PROBLEM ÇÖZME ORTAMI: LaDoPro
ÖNSÖZ
SEMBOL LİSTESİ
ŞEKİL LİSTESİ
ÖZET
SUMMARY
BÖLÜM 1. GİRİŞ
BÖLÜM 2. LAZER DOKU ETKİLEŞİMİ
1. Dokunun optik özellikleri
BÖLÜM 3. MONTE CARLO TEKNİĞİ
BÖLÜM 4. LaDoPro SİSTEMİ
4.2.1 Veri Yapıları
BÖLÜM 5. UYGULAMA ÖRNEĞİ
SONUÇLAR VE ÖNERİLER
ÖNSÖZ
Bu kısımda yardımlara göndermeler yapılacaktır.
SEMBOL LİSTESİ
Kullanılan semboller belirtilecektir.
ŞEKİL LİSTESİ
Ţekiller listelenecektir.
ÖZET
Çalışmanın özeti
SUMMARY
Çalışmanın İngilizce özeti
BÖLÜM 1. GİRİŞ
Problem çözme ortamlarının önemi belirtilecektir. Benzetimin görselleştirilmesinin getireceği yararlardan bahsedilecektir.
BÖLÜM 2. LAZER DOKU ETKİLEŞİMİ
Işık, madde ile etkileştiğinde, pek çok süreç oluşur. Işık emilime uğrayabilir, elestak olan veya olmayan saçılma olabilir, yansıma olabilir. Tüm bu süreçler dalga boyu bağımlıdır. Tez de; emilim, elastik saçılma ve yansıma göz önüne alınacaktır.
Yakın kızıl ötesi dalgaboyu bölgesinde, doku içinbdeki baskın süreç fotonların elastik saçılmasıdır. Elastik, süreçte fotonların enerjilerini değiştirmemesi demektir. Bir bütün olarak göz önüne alınırsa, ışık enerjisi bu tür saçılmadan dolayı kayıp olmaz. Ancak, bir saçılma ortamı geçilirken ileri doğrultuda zayıflama oalcaktır çünkü bazı fotonlar yeni yayılma doprultuları bulacaktır. Bu zayıflama üstel bir kanınla tarif edilebilir (Lambert-Beer kanunu) ve saçılmanın ölçüsü, m s saçılma katsayısı makroskopik parametresiyle gösterilebilir. Saçılma katsayısının birimi 1/uzunluk tur. Genelde mm-1 birimi kullanılır. Dolayısıyla, 1/m s, fotonun saçılma olayları arasında aldığı ortalama yolun bir ölçüsüdür. Dokuda değeri 10 mm-1 civarındadır.
Emilimi tarif etmek için kullanılan emilim katsayısı, m a, fotonun madde tarafından emilme olasılığının bir ölçüsüdür. Doku içi değeri 0.1 mm-1 civarındadır. Toplam zayıflama katsayısı aşağıdaki şekilde tanımlanır:
![]()
![]() Dokunun optik özelliklerini tarif eden eden üçüncü büyüklük saçılma anizotropi faktörü g dir.:
Dokunun optik özelliklerini tarif eden eden üçüncü büyüklük saçılma anizotropi faktörü g dir.:
Bu parametre saçılma açısının kosinüs ortalamasıdır. 1 ile 1 arası değişim gösterir. g = -1 değeri tam geri saçılma, g = 0 değeri izotropik saçılma, g = 1 değeri tam ileri saçılma demektir. Dalga boyundan daha büyük cisimlerce saçılmaya uğrayan ışık (doku durumundaki süreç), ileri saçılma gösterir. Işık saçılması anizotropisi Henyey- Greenstein faz fonksiyonunda, ilk olarak, yıldızlar arası toz bulutunda ışık saçılmasını tarif etmek için kullanılmıştır.
![]()
Burada p fonksiyonu, fotonun W dorultusunda ilerlerken, saçılma sonucu W doğrultusunda devam etme olasılığıdır, q sapma açısıdır. Tipik g değeri 0.7-0.95 arasındadır.
Diğer yararlı bir parametre indirgenmiş saçılma katsayısıdır:
![]()
Doğrusal iletim katsayısı aşağıdaki gibi tanımlanır:
![]()
BÖLÜM 3. MONTE CARLO TEKNİĞİ
Doku içindeki foton dağılımını hesaplama sorunu çeşitli yöntemlerle çözülmektedir. En çok kullanılan iki yöntem Monte Carlo benzetimi ve yayılım teorisidir.
Yayılım teorisi fiziksel sistemlerdeki pek çok iletim olayını (kütle, ses, ısı, elektromanyetik enerji) tarif eden iletim teorisinden türetilmiştir. Yayılım teorisi, temel olarak, özel bir iletim doğrultusunun seçilmediği ortamlar için tercih edilmektedir. Buna göre, foton saçılması durumunda doğrultu değiştiren her foton düzgün bir olasılık dağılımıyla hareket eder. Bir başka deyişle, doku içine bir algılayıcı yerleştirilseydi her doğrultuda, ışık kaynağı ko
numundan bağımsız olarak, eşit miktarda foton algılayacaktı. Saçılma ortamındaki foton yoğunluğunu farksal denklemler ile çözmeyi amaçlar. Bu basitleştirme, sürecin mantığını anlamak için yeterli olmakla birlikte her zaman doğru değildir.Monte Carlo benzetimi ise çok farklı bir yaklaşım kullanır. Ortamdaki her bir foton hareketinin benzetimini amaçlar. Saçılma süreci oldukça stokastiktir. Benzetim için rastgele sayı üretecini gerektirir. Bu şekilde çok sayıda foton üretilerek sonunda bir dağılım elde edilir. Yayılım teorisindeki kısıtlar Monte Carlo yöntemi için geçerli değildir. Foton saçılmalarını onaylamak için rastgele sayıların üretildiği olasılık dağılımı belirlenebilir.
Doku içi ışık yayılımını modellemek için Monte Carlo benzetimi genişçe kullanılmaktadır. Ünlü gazino oyunlarından ismini alan bu teknik, karışık tipte rastgele adımların içerildiği istatistiki yöntemlere dayanır. İlk ağırlıklı bir foton paketi benzeştirilecek dokuya fırlatılır. Her etkileşim noktasınd
a, bir sonraki etkileşim noktasına saçılma doğrultusu, emilim ve uzaklık; dokunun optik özelliklerine dayanılarak stokastik değişkenler olarak hesaplanır. Ardından ağırlık güncellenir ve paket bir sonraki etkileţim noktasına hareket ettirilir. Bu seyahat sırasında foton paketinin fiziksel parametreleri kaydedilebilir, böylece büyük foton paketlerinin davranışı ilgilenilen makroskopik parametrelerin istatistiki bir umusu olur.Benzetim, ışık yaılımının modellenmesi için güçlü bir yöntemdir. Yayılım denkleminin getirdiği yetersizliklerle karşılaşmaz. Herhangi bir geometriyi dahi benzeştirerek gerçekçi sonuçlar elde edilebilir. Ancak, çok büyük bir dezavantajı vardır ki, pratik uygulamalarda kullanılmasında sakınca yaratabilir: Hesapsal olarak çok fazla zaman
gerektirir. İstatistiksel bir yöntem olduğu için, daha fazla foton paketinin kullanılması varyansı düşürerek sonucu iyileştirir. Sağlıklı sonuçlar elde etmek için hızlı makinelerde bile saatler gerekebilir.Sınır koşullarını benzetime eklemek dahil etmek oldukça kolaydır: Fresnel ve Snell kanunları, foton paketi sınıra çarpınca kullanılır.
BÖLÜM 4. LaDoPro SİSTEMİ
4.2.1 Veri Yapıları
Giriş parametreleri, daha önce hazırlanmış bir dosyadan okunabileceği gibi ara yüzden de girilebilir. Bunun sonucunda benzetim başlatılır. Bu parametreler; ortamın geometrik ve optik parametreleri, sonuç dizi boyutu ızgara genişliği, zaman çözünürlüğü, zaman adımı sayısı, fotn kaynağının konumu ve hesaplara girecek foton sayısıdır. Bu giriş parametreleri özel bir yapıda saklanabilir.
Bir diğer yapı çıkış parametrelerinin kotarılması için oluşturulmuştur. Bir dizi foton paketini kayıt için, bir diğeri sonuçları tutmak içindir. Algılanan fotonların toplam ağırlığı, her zaman adımı için, bir dizide tutulur; böylece algılama şiddeti zamanın fonksiyonu olarak değerlendirilebilir. Algılanan foton paketlerinin sayısı, her zaman adımında ayrıca kaydedilir, böylece istatistiğin kalitesi hakkında bilgi sahibi olunmuş olur.
Üçünci bir yapı, benzetim sırasında, foton paketinin özelliklerini izlemek için kullanılacaktır. Foton paketinin konum bilgisi (x,y,z), zaman bilgisi (t), doğrultu bilgisi (ux,uy,uz), ağırlık bilgisi (w) bu yapıda tutulacaktır. Mantıksal bir değişkenle foton paketinin "yaşam" bilgisi tutulur. Bu durum sınırların geçilmesi veya ortam tarafından tamamen emilmesi durumunda geçerlidir.
![]() Benzetim başladığında; foton paketine konum, doğrultu ve birim yük ataması yapılır. Yeni etkileşim noktasına olan uzaklık aşağıdaki formülle hesaplanır:
Benzetim başladığında; foton paketine konum, doğrultu ve birim yük ataması yapılır. Yeni etkileşim noktasına olan uzaklık aşağıdaki formülle hesaplanır:
Formüldeki R, 0-1 arası rastgele bir sayıdır. Rastele üretecinin tanım gereği görevini yaptığından emin olmak için programa ayrıca rastgele sayı üreteci kodu eklenebilir.
![]() Bir sonraki adımda, foton paketinini hedef adım yolunda sınırlara çarpıp çarpmadığı kontrol edilir. Çarpmadığı varsayılarak, paket hareket ettirilir ve ağırlığı,w, aşağıdaki oran kadar azaltılır.
Bir sonraki adımda, foton paketinini hedef adım yolunda sınırlara çarpıp çarpmadığı kontrol edilir. Çarpmadığı varsayılarak, paket hareket ettirilir ve ağırlığı,w, aşağıdaki oran kadar azaltılır.
Kayıt dizisindeki ilgili konum bir birim arttırılır. Böylece paketin konumu güncellenmiş olur. Geçen toplam süre S/v kadar artar. Burada v ışığın ortamdaki hızıdır.
Çevrimi kapatmak için gereken son adım, paket için yeni bir doğrultu belirlemektir. Azimut saçılama açısı, j
= 2p R olarak hesaplanır. Burada R daha önce belirtilen rastgele bir sayıdır. Saptırma saçılma açısı, q , Henyey-Greenstein distribution dağılımıyla hesaplanır. İzotropik saçılma durumunda sapma açısı en basti şekliyle hesaplanır: q = p R.Yukarıda belirtilen üç adım; hoton paketinin yeni etkileşim noktasına hareket ettirilmesi, foton paketinin özelliklerinin değiştirilmesi ve yeni bir yayılma doğrulutusu hesaplanması benzetimin belkemiğidir ve genel programın en fazla işlemciyi meşgul eden kısmıdır. Program
performansının iyileştirilmesi, en fazla bu ü adım üzerinde çaba harcamayı gerektirir.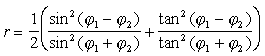 Varsayalım ki paket sınıra çarptı, bu durumda iki olasılık söz konusudur. Sınırın öbür tarafı saçıcıdır veya değildir. İlk durumda S uzaklığı bölünür ve paket sınıra doğru hareket eder, ve o noktada Fresnel yansıma olasılığı söz konusu olur. Tekrar, rastgele bir sayı çekilir, ardından aşağıdaki denklemlerle belirlenen r yansıma katsayısıyla karşılaştırma yapılır:
Varsayalım ki paket sınıra çarptı, bu durumda iki olasılık söz konusudur. Sınırın öbür tarafı saçıcıdır veya değildir. İlk durumda S uzaklığı bölünür ve paket sınıra doğru hareket eder, ve o noktada Fresnel yansıma olasılığı söz konusu olur. Tekrar, rastgele bir sayı çekilir, ardından aşağıdaki denklemlerle belirlenen r yansıma katsayısıyla karşılaştırma yapılır:
![]()
Testin sonucuna göre, paket ilerleyerek ortam değiştirir veya geldiği ortama geri yansır.
Eğer diğer ortam saçılma yapmayan türden ise, foton paketi sınıra doğru yine hareket eder ve Fresnel yansıma testini görür. İletilmesi durumunda örneği terkeder ve sonlanır.
Foton paketinin ortamce emilmesi durumu da incelenmiştir. Ağırlık, belirli bir limit eşiğin altına düşerse, varlığı gereksiz bir hesap yükü ve zaman yükü getireceği için, paket sonlandırılır. Böyle bir gerçekleme fiziksel olarak anlamsızdır, zira bir kısım enerji süreö sırasında keybedilmiş olacaktır. Bunun için, sonlandırma ayrı bir rutinde kotarılır (Rulet). Paketin yok olması büyük bir ihitimaldir ( p = 0.9 gibi). Paket yaşarsa (0.1 olasılık), ağırlığı 1/(1
- p) kadar artırılır (burada 10 değeri)ve devam etmesine izin verilir.Tüm foton paketleri fırlatılıp bir şekilde sonlandırıldığında, benzetim sona erer ve program sonuç dizisini bir çıkış dosyasına veya ekrana gönderir.
Hesap süreçleri ve bilgi giriş/çıkış işlemleri bu kısımda belirtilecektir.
BÖLÜM 5. UYGULAMA ÖRNEĞİ
SONUÇLAR VE ÖNERİLER