Colisões
Marcos Portnoi
Rafael G. B. Araújo
Romildo Fausto
Victory Fernandes
Engenharia Elétrica - UNIFACS
25.Setembro.1999
http://surf.to/locksmith
--
Paulo FrancisIndíce *Objetivos *Introdução *Parte Experimental *
Material Utilizado *Procedimento e Discussão *Conclusão *Referência *
Através de atividades realizadas numa rampa de lançamentos horizontais, estudar a conservação do momento linear de um corpo, identificar e representar vetorialmente a quantidade de movimento deste corpo e obter vetores resultantes vetoriais de quantidade de movimento na horizontal.
Atua em uma colisão uma força relativamente grande durante um intervalo de tempo comparativamente curto, em cada corpo que se choca. Como dois aspectos básicos que caracterizam uma colisão, tem-se a mudança brusca do movimento de ambas ou de pelo menos uma partícula que se choca e a distinção dos tempos "antes da colisão" e "depois da colisão" é clara.
Durante a colisão de duas bolinhas de vidro, por exemplo, o início e o fim da colisão podem ser determinados com precisão. O contato entre as duas bolinhas acontece num intervalo de tempo muito curto se comparado com o tempo de observação das duas bolas. Outro exemplo clássico é o bastão de beisebol batendo numa bola. O bastão exerce na bola uma força muito grande e tanto o bastão como a bola se deformam durante a colisão. As forças que atuam em intervalos de tempo muito menores que o tempo de observação do sistema são denominadas em Física de forças impulsivas.
A equação matemática que relaciona impulso e momento pode ser obtida pelo método diferencial ou sem utilizá-lo. Pelo método diferencial, tomando a Segunda Lei de Newton, tem-se que F = dp/dt, onde dp é a variação infinitesimal do momento. Tomando dp=Fdt, pode-se determinar a variação do momento durante o choque. Assim, vem:
O primeiro membro da equação é a variação do momento, pf – pi; o segundo membro intitula-se impulso J da força. Assim,
ou,
J = pf - pi
O Teorema Impulso-Momento enuncia que:
O impulso da força resultante que atua numa partícula durante determinado intervalo de tempo é igual à variação do momento da partícula durante esse intervalo.
De outra forma, se F = ma, então:
O produto F.D t é a impulsão J. Ainda, o produto m.D v pode ser escrito como m.vf – mvi, e o produto m.v e definido como a quantidade de movimento linear p. Assim,
Durante uma colisão de duração diminuta, o momento das partículas se conserva, ou seja, o vetor momento inicial é igual ao vetor momento final. Assim sendo, não havendo forças externas aplicadas às particulas, o momento total do sistema de duas partículas não será alterado pela colisão.
Pode-se determinar duas categorias especiais de colisão: elásticas e inelásticas.
Nas colisões elásticas, a energia cinética inicial é igual à energia cinética final do sistema. Ou seja, não há forças dissipativas consideráveis. Numa colisão inelástica, a energia assume outras formas, podendo ser armazenada como energia interna pelo sistema ou então alguma energia interna pode ser liberada, de maneira que a energia cinética inicial não é igual à energia cinética final do sistema.
Em ambos os casos, entretanto, o momento linear é sempre conservado.
Os experimentos a seguir poderão demonstrar que o momento linear é conservado em colisões. Estudar-se-á especificamente a conservação de movimento numa colisão frontal de duas esferas.
Nota: A gravidade local g usada em todos os cálculos foi de 9,7833 m/s2
.Uma rampa de lançamentos com escala de posicionamento, haste, suporte regulável de apoio da esfera alvo com quatro graus de liberdade referência 7743.04.B e mufa abraçante para regulagem de altura, fabricado pela Maxwell Metalurgia e Equipamentos Científicos Ltda.
A Figura 1 traz um esquema da rampa de lançamentos utilizada para os experimentos. Determinou-se primeiramente a massa das duas esferas e a altura h’’ no ponto em que a esfera deixa a rampa e inicia a queda livre. Seja mm a massa da esfera metálica, e mv a massa da esfera de vidro.
mm = 0,016 Kg
mv = 0,00858 Kg
h’’ = 25 cm
À frente da rampa de lançamento, foram colocadas as duas folhas de papel ofício e afixadas sobre a mesa, com auxílio de fita adesiva. A esfera de vidro foi então posicionada logo à frente da saída da rampa de lançamento, apoiada sobre o suporte afixado no conjunto, de modo que a esfera de metal se choque frontamente com ela, assim que deixar a rampa. Marcou-se então sobre o papel ofício o ponto X0, correspondente à reta vertical que corta o centro da esfera de vidro e o papel logo abaixo. Ver Figura 2.
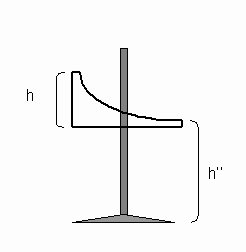
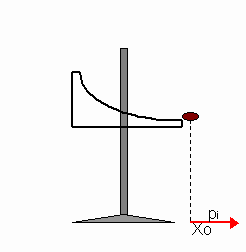
Figura 1: Rampa de lançamentos. Figura 2: Esfera de vidro posicionada no ponto Xo.
Uma vez determinado o ponto X0, a esfera de vidro foi novamente retirada. Agora, posicionou-se a esfera metálica 10 cm acima do ponto de saída da rampa de lançamento, ou seja, a altura h na Figura 1. Pode-se calcular a velocidade de saída da esfera metálica neste ponto, usando a relação:
Esta relação é obtida do Princípio da Conservação de Energia, onde a energia potencial da esfera quando no topo é igual à somatória da energia cinética ao sair da rampa e a energia cinética rotacional. Assim,
Convertendo as grandezas da dinâmica rotacional para seus equivalentes lineares, usando a inércia rotacional para uma esfera sólida e resolvendo para v, obtém-se a relação indicada. Assim sendo, a velocidade de lançamento ou escape da esfera metálica é:
Colocou-se as folhas de papel carbono sobre as folhas brancas de papel ofício, viradas para baixo, de modo que a esfera metálica, ao se chocar com a mesa sobre as folhas, faça uma marca na folha branca de papel ofício. Foram feitos cinco lançamentos da mesma altura h. Com auxílio da régua, traçou-se um retângulo que englobasse as marcas de todos esses cinco lançamento. Este retângulo é a área de imprecisão do lançamento. O centro dele corresponde ao valor mais provável, que foi então assinalado como Xc. Traçou-se uma reta suporte de X0 a Xc. Esta reta suportará os vetores quantidade de movimento das esferas e servirá de auxílio para colher as medidas de alcance das duas esferas após os choques.
O vetor quantidade de movimento inicial pi da esfera metálica é paralelo à essa reta suporte, e tem módulo conforme abaixo:
Veja também a Figura 2 para o vetor pi.
Este é o momento para então colocar-se a esfera de vidro em seu local apropriado, em frente ao escape da rampa de lançamentos. A esfera metálica foi posicionada 10 cm acima e abandonada. Em poucos instantes, esta desceu a rampa e chocou-se com a esfera de vidro abaixo. As duas projetaram-se para frente e caíram por sobre o papel carbono, a esfera de vidro mais adiante.
Retirando-se o papel carbono, assinalou-se os pontos 1v e 1m onde as esferas de vidro e metálica, respectivamente, tocaram o papel branco. Repetiu-se a colisão mais três vezes e, retirando-se o papel carbono, marcou-se os novos pontos de choque como sendo 2v, 3v, 4v, 2m, 3m e 4m. Um dos pontos da esfera metálica foi desconsiderado, por estar bem distante em relação aos demais, e então traçou-se o retângulo de imprecisão para os pontos m e v. Os centros foram então localizados com auxílio da régua e marcados como cv e cm, para as esferas de vidro e metal, respectivamente.
Os vetores descolamento horizontal de cada esfera têm a mesma direção e sentido, paralelos ao vetor quantidade de movimento pi, e tiveram módulos conforme abaixo:
d1 = 8,7 cm
d2 = 30,7 cm
sendo que d1 é o vetor deslocamento da esfera metálica, e d2 é o vetor deslocamento da esfera de vidro. (Os números de imprecisão foram desconsiderados nos cálculos, de forma a simplificar as operações. Os erros não estão sendo, por conseguinte, propagados.)
O próximo passo consiste em calcular o tempo de vôo ou queda das duas esferas, que são idênticos (pois as duas esferas iniciam a queda da mesma altura). Utilizando a equação de cinemática adaptada para queda livre, faz-se o cálculo.
Agora as velocidades vx1 e vx2 das esferas de metal e vidro, respectivamente, podem ser calculadas.
Em seguida, calculou-se os módulos dos vetores quantidade de movimento pm e pv (metal e vidro) de cada esfera.
Estes vetores têm a mesma direção e sentido do vetor pi, conforme indicado na Figura 2. O vetor quantidade de movimento resultante, pr, é igual à soma vetorial de pm e pv. Portanto,
O vetor pr representa a quantidade de movimento linear total das duas esferas após o choque, que por definição, é igual à quantidade de movimento linear das duas esferas antes do choque. Como, antes do choque, a esfera de vidro está parada e apenas a esfera metálica tem movimento, o vetor quantidade de movimento inicial é igual à quantidade de movimento da esfera metálica ao abandonar a rampa de lançamento, que foi calculado anteriormente: o vetor pi. O vetor pr deve portanto ter módulo igual ao vetor pi.
No experimento relatado, os valores encontrados foram 0,019 Kg.m/s e 0,017 Kg.m/s como quantidades de movimento inicial e final. O erro é de:
O erro encontrado de 10,5% é extremamente razoável para as condições do experimento, onde foram desconsideradas as forças dissipativas de atrito, não houve propagação de erros e trabalhou-se com instrumentos de medida de precisão mediana. Deste modo, pode-se considerar que o valor achado para quantidade de movimento final, bastante próximo da quantidade de movimento inicial do sistema conforme calculado, vem a comprovar a lei da conservação da quantidade de movimento numa colisão frontal.
Os experimentos realizados puderam demonstrar que o princípio da conservação da quantidade de movimento aplica-se indiscutivelmente numa colisão frontal. Fazendo colidir duas esferas de materiais diferentes, tendo suas velocidades iniciais e finais sob controle, foi possível obter ambos valores para quantidade de movimento inicial e final do sistema, e o erro experimental dos valores calculados significou sua obediência ao princípio da convervação.
Vislumbrados à luz da prática, comprovados por cálculos realizados pessoalmente, os conceitos de conservação de momento estão fácil e completamente fixados.
Halliday, David et al. (1992) Física 1; vol. I, 4. Edição; LTC Livros Técnicos e Científicos S.A., Rio De Janeiro, RJ; p. 167 a 180, 193 a 197 e 228 a 240.