Estequiometria

Através de uma reação de precipitação, observar e comprovar as leis das transformações químicas ou leis ponderais das reações, especificamente a Lei da Conservação de Massa de Lavoisier e a Lei das Proporções Definidas de Proust. Com base nas leis, realizar cálculos tomando como base a equação balanceada da reação e comparar dados experimentais com dados tabelados.

Estequiometria significa "medir os constituintes elementares". A estequiometria constitui-se na base para o estudo quantitativo das reações e substâncias químicas. É possível, de posse de uma equação balanceada que representa uma reação química, prever-se com extrema precisão as quantidades de cada produto gerado, ou ainda, determinar as quantidades necessárias de reagentes de modo a produzir determinada quantidade de produtos. Por fim, é possível calcular os rendimentos dos produtos e a eficiência geral do processo.

Dois conceitos norteiam os cálculos estequiométricos. O primeiro deles foi introduzido por A. L. Lavoisier em 1774, conhecido hoje como a Lei da Conservação de Massa de Lavoisier. Trabalhando principalmente com balanças, Lavoisier verificou que a massa dos reagentes numa reação era a mesma massa encontrada nos produtos, após a reação. Assim sendo, se havia alguma perda de massa, essa não era mensurável. Essa observação é a origem do conceito popular de que "na Natureza nada se destrói, tudo se transforma."

O enunciado da lei diz que a soma das massas antes da reação é igual à soma das massas após a reação, ou que o ganho ou perda de massa numa reação não é mensurável. Na realidade, em reações nucleares onde há extrema liberação de energia, pode haver de fato redução de massa para os produtos. O físico Albert Einstein permitiu que isso fosse perfeitamente compreensível e mensurável de acordo com sua equação que relaciona energia e matéria: E = mc²,

onde E é a energia, m é a massa e c é a velocidade da luz no vácuo. Dessa maneira, massa e energia podem ser considerados como uma coisa única, ou ainda interconversíveis. A massa não é perdida, mas convertida em energia.

O segundo conceito é conhecido como a Lei da Composição Definida ou Lei das Proporções Constantes. Esse conceito descreve a mais importante propriedade de um composto, sua composição fixa: Cada componente de um composto tem sua composição em massa definida e característica. Ainda, a Lei postula que a proporção de massas que reagem permanece constante e fixa. Essa lei foi proposta pelo químico L. J. Proust em 1801, e assim leva seu nome, Lei de Proust, e deu origem ao cálculo estequiométrico. Vejamos abaixo uma aplicação dessas duas leis. Seja a reação:

4Fe(s) + 3O₂(g) à 2Fe₂O₃(s)

que representa ferro reagindo com oxigênio para formar óxido de ferro. A Lei de Proust permite afirmar que os coeficientes estequiométricos, ou seja, os números que antecedem cada composto ou substância são exatamente as proporções ou razões fixas das quantidades dos reagentes e produtos. Isso equivale dizer que 4 átomos de ferro reagem com 3 moléculas de oxigênio para formar 2 unidades de óxido de ferro. Ou ainda, que 4 mols de átomos de ferro reagem com 3 mols de moléculas de oxigênio para formar 2 mols de óxido de ferro. A proporção de 4:3:2 é fixa.

E de acordo com a Lei de Lavoisier, a massa de 4 átomos ou mols de ferro mais a massa de 3 mols ou moléculas de oxigênio será igual à massa de 2 mols ou unidades de óxido de ferro. Isso significa que, havendo uma quantidade adicional de qualquer um dos reagentes (um excesso) além da proporção estequiométrica, este excesso não reagirá. Por exemplo, se 5 mol de átomos de ferro e 3 mols de moléculas de oxigênio estiverem presentes no início da reação anterior, somente 4 mols de átomos de ferro reagirão, deixando ao final 1 mol de átomos sem reagir. Diz-se que o ferro encontra-se em excesso. Tendo-se a massa de oxigênio e de ferro que vão reagir, pode-se prever exatamente a massa que sobrará de ferro sem reagir ao "final" da reação. Verificaremos esses cálculos em detalhes na discussão do experimento a seguir.

Vidraria: 3 béquers de 100ml, pipeta volumétrica, bastão de vidro.

Reagentes: cloreto de bário 1,0 mol/l, ácido sulfúrico 1,2 mol/l.

Equipamentos: balança.

Materiais diversos: espátula.

Numerou-se três béquers limpos e secos de 1 a 3 e pesou-se cada um. As massas foram respectivamente:

m_béquer1 = 41,14g

m_béquer2 = 49,65g

m_béquer3 = 49,46g

Com auxílio da pipeta, transferiu-se 10ml da solução de cloreto de bário 1,0 mol/l para o béquer 1. Pesou-se novamente este béquer com o sal, obtendo-se:

m₁ = 52,86g

A massa da solução de sal é portanto:

m_sal = m₁ – m_béquer1

m_sal = 11,72g

Novamente com a pipeta, transferiu-se 10ml de solução de ácido sulfúrico 1,2 mol/l para o béquer 2, pesando-se o conjunto em seguida.

m₂ = 60,44g

Portanto a massa da solução de ácido é:

m_ácido = m₂ – m_béquer2

m_ácido = 10,79g

Transferiu-se agora todo o conteúdo do béquer 1 (solução de cloreto de bário) para o béquer 3, e logo após transferiu-se lentamente o conteúdo do béquer 2 (solução de ácido sulfúrico) para o béquer 3. De imediato observa-se a formação de precipitado branco e fino, que é o sulfato de bário, segundo a equação abaixo:

BaCl₂ + H₂SO₄ à BaSO₄ ¯ + 2HCl

Após leve agitação, pesou-se o béquer 3 e calculou-se a massa de produtos contida nele:

m₃ = 71,62g

m_produtos = m₃ – m_béquer3 = 22,16g

Analisemos na Discussão a seguir o resultado encontrado e o esperado.

Segundo a lei de Lavoisier, é de se prever que, neste experimento, a massa obtida no béquer 3 deve ser igual à soma das massas dos reagentes nos béquers 1 e 2, uma vez que não há perda de matéria.

Somando as massas de solução de cloreto de bário e ácido sulfúrico utilizados como reagentes, temos:

m_sal + m_ácido = 11,72 + 10,79 = 22,51g

A massa obtida ao final da reação foi de 22,16g, ou seja, contendo erro de 1,6%. Este é um indicativo bastante razoável da eficácia da lei da conservação de massa, pois há várias fontes de erro no experimento que podem haver causado a diferença de 1,6%. Uma delas é a própria balança, que não é de extrema precisão, apresentando flutuações visíveis na medição. Em adição, uma parte de reagentes ficou nos béquers originais, mesmo que algumas gotas, provocando diminuição da massa a reagir. E por final, parte do precipitado pode ter ficado nas paredes do béquer 3, não passando para o papel de filtro. Essa perda de massa, entretanto, deve ser muito pequena, visto que a massa obtida de sulfato de bário e que será comprovada na Parte II adiante foi bastante próxima da prevista. (ver questionário.)

O erro de 1,6% é pequeno, entretanto, para os objetivos do experimento. Pode-se considerar que a massa foi conservada na reação. Utilizemos agora o produto da reação para comprovação da lei de Proust.

Vidraria: 1 béquer de 100ml, placa de petri, funil, bastão de vidro, vidro de relógio.

Reagentes: produto da reação do experimento anterior (sulfato de bário principalmente).

Equipamentos: balança, suporte metálico para funil.

Materiais diversos: papel de filtro diâmetro 12cm, pisseta.

Pesou-se inicialmente o papel de filtro:

m₁ = 1,05g

Com o bastão de vidro, agitou-se a mistura produzida no experimento anterior e então escoou-se esta mistura, através do papel de filtro e funil, lentamente com auxílio do bastão de vidro. Lavou-se o interior do béquer com a pisseta, de modo a recuperar o máximo possível de mistura para o papel de filtro.

Após o escoamento da mistura através do papel de filtro, retirou-se este do funil e foi então colocado sobre a placa de petri. Cobriu-se essa placa de petri com um vidro de relógio e deixou-se o conjunto em descanso por uma semana. Sobre o papel de filtro, ficou o precipitado branco úmido.

Uma semana após, o papel de filtro com o precipitado recolhido sobre ele estava seco. Recolheu-se o papel da placa de petri e e foi então levado à balança para pesagem.

m₂ = 3,39g

Vejamos na Discussão a seguir como o resultado foi interpretado.

De posse da massa do papel de filtro e da massa de resíduo com papel, é possível obter a massa de sulfato de bário produzida no experimento.

m_BaSO4 = 3,39 – 1,05 = 2,34g

A fim de calcular a massa de sulfato de bário que se deveria ter obtido, lancemos mão do cálculo estequiométrico.

Primeiro, calcula-se a massa de cloreto de bário que foi usada no experimento. Para isso, usamos a relação:

onde M é a concentração molar, m é a massa a ser calculada, V é o volume utilizado da solução em litros e MM é a massa molecular da substância obtida na tabela periódica.

Assim, sendo, obtemos para a massa de cloreto de bário:

Através de uma regra de três simples, podemos então prever qual a massa que deveria ser produzida de sulfato de bário na reação. Leva-se em conta a proporção estequiométrica de 1:1:1:2 e utiliza-se as massas moleculares dos compostos obtidas na tabela periódica. Na equação abaixo as massas moleculares estão entre parêntesis ao lado de cada composto.

BaCl_{2 (208,3)} + H₂SO_{4 (98,1)} à BaSO_{4 (233,40)} ¯ + 2HCl₍₇₅₎

Relacionamos agora a massa de 1 mol de cloreto de bário com 1 mol de sulfato de bário, e 2,083g de cloreto de bário utilizados em uma regra de três a fim de calcular a massa de sulfato de bário correspondente.

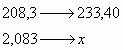
Com base nas leis de conservação de massa e das proporções definidas, podemos relacionar as grandezas e razões estequiométricas para efetuar os cálculos matemáticos. Assim, espera-se encontrar ao final dessa reação 2,334g de sulfato de bário. A massa obtida na balança de nosso experimento foi de 2,34g, um erro experimental muito baixo de 0,26%. A lei das proporções definidas mostra sua eficácia e utilidade.

Procedamos agora às respostas para o questionário proposto no guia do experimento.

Vários fatores podem ter contribuído para o erro de 1,6% encontrado na pesagem de massa de produtos e reagentes no experimento. Um deles é a própria balança, que não é de extrema precisão, apresentando flutuações visíveis na medição. Em adição, uma parte de reagentes ficou nos béquers originais, mesmo que algumas gotas, provocando diminuição da massa a reagir. E por final, parte do precipitado pode ter ficado nas paredes do béquer 3, não passando para o papel de filtro. Essa perda de massa, entretanto, deve ser muito pequena, visto que a massa obtida de sulfato de bário e comprovada na Parte II foi bastante próxima da prevista.

b) Quais as massas de ácido sulfúrico e cloreto de bário utilizados no experimento para a síntese do sulfato de bário?

Novamente, usamos a relação abaixo a fim de calcular as massas utilizadas, partindo da concentração molar de cada solução e das massas moleculares obtidas na tabela periódica. (os valores estão expressos anteriormente neste relatório).

Para o cloreto de bário 1,0 mol/l:

de cloreto de bário.

Para o ácido sulfúrico:

de ácido sulfúrico.

c) Qual reagente está em excesso na reação? Justifique através de cálculos.

Em análise da reação, podemos observar que o cloreto de bário reage com o ácido sulfúrico na proporção de 1:1, ou seja, um mol de cloreto de bário reage com 1 mol de ácido sulfúrico.

Utilizou-se no experimento volumes iguais de cada solução, 10ml. Entretanto, a solução de ácido sulfúrico é mais concentrada que a de cloreto de bário, conforme suas concentrações molares respectivas de 1,2 mol/l e 1,0 mol/l. Então, é de se concluir que há mais mols (cerca de 20% a mais) de ácido sulfúrico para reagir com cloreto de bário que a razão estequiométrica, uma vez que os volumes são iguais. Com efeito, utilizemos a regra de três de modo a relacionar as massas moleculares da equação com as massas obtidas na balança. A pergunta é, quantos gramas de ácido sulfúrico são necessários para obter 2,334g de BaSO₄, se 98,1g de H₂SO₄ geram 233,40g de BaSO₄?

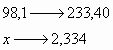
de H₂SO_4.

Assim, são necessários 0,981g de ácido sulfúrico para reagir e obter 2,334g de sulfato de bário. Pela questão anterior, verifica-se que foram utilizados 1,1772g de ácido sulfúrico. Com efeito, o ácido está em excesso na reação, e o excesso além da proporção estequiométrica não vai reagir com o cloreto de bário.

Usando o mesmo cálculo para o cloreto de bário, chega-se a uma massa de 2,083g necessária para produzir 2,334g de sulfato de bário. A massa de 2,083g foi exatamente a utilizada no experimento, o que mostra que o cloreto de bário não está em excesso.

d) Qual a massa de BaSO₄ obtida experimentalmente? Qual seu erro experimental?

A massa foi de sulfato de bário obtida em nosso experimento foi de 2,34g, representando um erro experimental de 0,26% em relação à massa que deveria ser obtida segundo o cálculo estequiométrico e as massas moleculares (2,334g). (ver Parte II.)

Os experimentos realizados puderam confirmar a veracidade e eficácia da lei da conservação de massa de Lavoisier e da lei das proporções definidas ou Lei de Proust. Com base nos conceitos propostos por essas leis, pode-se realizar cálculos que previam resultados dos experimentos, e pode-se verificar que os resultados aproximavam-se com excelente precisão dos valores previstos.

O poder e utilidade do cálculo estequiométrico, que em sua essência é simples, ao relacionar razões pela ferramenta matemática da regra de três, foi presenciado e experimentado no volume suficiente para fixá-lo como conhecimento e prática.

Russel, John Blair. (1994) Química Geral; vol. I, 2. Edição; Makron Books, São Paulo; p. 16 a 17 e 74 a 79.

Feltre, Ricardo. (1990). Fundamentos da Química; vol. Único, 1. Edição; Ed. Moderna Ltda., São Paulo; p. 133 a 136.