Gases
Rafael G. B. Araújo
Rafael Pereira dos Santos
Marcos PortnoiEngenharia Elétrica - UNIFACS
05.Junho.1999
Objetivos
Observar propriedades do estado gasoso da matéria através de reação de formação de um gás e reação entre gases. Coletar e medir o volume do gás obtido numa reação, aplicando e demonstrando a lei de Dalton. Estudar a velocidade de difusão dos gases com base em experimento, demonstrando e aplicando a Lei de Graham. Comparar os resultados obtidos experimentalmente com os dados previstos teoricamente.
Introdução
Gás
é um dos três estados da matéria, ou um dos cinco estados, se se considerar o plasma e o Condensado de Bose-Einstein como estados. Um gás é definido como uma substância que se expande espontaneamente para preencher completamente seu recipiente de maneira uniforme. Neste estado, as forças de atração intermoleculares são fracas, pois as moléculas estão muito distantes umas das outras, e talvez nem se toquem durante a maior parte do tempo. Essas forças fracas permitem uma movimentação rápida e independente das moléculas, o que praticamente dá a um gás um comportamento físico não dependente de sua composição química. Ainda, vários gases são muito semelhantes nessas propriedades físicas, donde surge a expressão gás ideal. Um gás ideal é aquele que serve de padrão de referência contra o qual os demais gases podem ser comparados. As leis dos gases são aplicadas a um comportamento previsto dum gás ideal, e os resultados experimentais podem ser contra eles comparados, e os resultados são surpreendentemente similares com gases diferentes. Ao se trabalhar com temperaturas e pressão extremas, entretanto, a aproximação do gás ideal já não é suficiente.Três variáveis são usadas para descrever o comportamento dos gases: pressão (P), temperatura (T) e volume (V). Segundo a lei combinada dos gases, assim chamada por combinar as leis de Charles (que afirma que, a pressão constante, o volume ocupado por uma quantidade de gás é diretamente proporcional a sua temperatura absoluta Kelvin) e Boyle (à temperatura constante, o volume ocupado por um determinado número de mols de um gás e inversamente proporcional à sua pressão), a pressão, temperatura e volume se relacionam no formato P1V1/T1=P2V2/T2, onde o subíndice 1 indica estado inicial e o 2 indica estado final de um gás. Assim sendo, quando variam temperatura, pressão e volume, a razão da pressão vezes o volume para temperatura permanece constante. (De maneira simples, a Lei de Charles pode ser expressa como o volume de um gás varia conforme sua temperatura, e a Lei de Boyle como com o aumento de temperatura de um gás, seu volume diminui).
Ainda é possível trabalhar com essa equação, chegando a uma expressão que define o gás ideal. Para isso, tomemos o enunciado da Lei de Gay-Lussac da combinação dos volumes e o Princípio de Avogadro.
Na reação abaixo, observa-se que quando os gases hidrogênio e oxigênio reagem para produzir água, existe uma relação entre os volumes dos reagentes e produtos, relação esta simples é constante, se mantidas as mesmas condições de pressão e temperatura.
2H2(g) + O2(g) à 2H2O(g)
O que equivale dizer que 2 volumes de hidrogênio reagem com 1 volume de oxigênio, produzindo dois volumes de água gasosa. Da observação deste fenômeno, vem a proposição da Lei de Gay-Lussac: quando medidos sob as mesmas condições de temperatura e pressão, os volumes dos reagentes e produtos gasosos de uma reação estão na mesma razão de números inteiros e pequenos.
Segundo sugestão feita por Avogadro em 1811, a relação dos volumes dos gases na reação é idêntica ao número de moléculas das substâncias, conforme demonstrado na equação de reação, porque volumes iguais de gases diferentes contém o mesmo número de moléculas quando medidos nas mesmas condições de temperatura e pressão. Este é o enunciado do Princípio de Avogadro. Assim sendo, o volume de uma amostra de qualquer gás é proporcional ao número de mols de moléculas da amostra.
Combinando as proporcionalidades 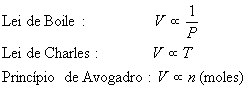
chegamos à relação ![]()
que pode ser reescrita no formato da equação ![]() ou
ou ![]()
onde R é uma constante de proporcionalidade conhecida como constante do gás ideal, e que assume valores diferentes para diversos gases. Esta equação ou relação é conhecida como lei do gás ideal. O fato de que a constante R muda de acordo com o gás empregado demonstra que os gases não são verdadeiramente ideais.
Em 1801, o professor inglês John Dalton observou que gases diferentes em uma mistura exercem pressão nas paredes do recipiente, de forma independente um do outro, e que a pressão medida dessa mistura de gases poderia ser calculada pela soma das pressões individuais de cada gás, se estes estivessem isolados no recipiente. Essa observação originou a Lei de Dalton das Pressões Parciais, que estabelece que a pressão total exercida por uma mistura de gases é igual à soma das pressões parciais dos gases individuais. Assim, Pgás 1 + Pgás 2 = Ptotal.
Duas outras propriedades dos gases podem ser observadas em experimentos ou no cotidiano, e uma delas será alvo de estudo neste relatório. Essas propriedades são a efusão e a difusão, e foram estudadas e definidas por Graham.
Difusão é a passagem de uma substância através de outra. Para os gases, este é um processo relativamente veloz, se comparado com os estados líquidos e sólidos. Thomas Graham, químico inglês, mediu em 1829 as velocidades de difusão de gases. Apoiado nesses dados, estabeleceu-se a Lei de Difusão de Graham, onde a velocidade de difusão de um gás através de outro é inversamente proporcional à raiz quadrada da densidade do gás, ou, de maneira ampliada, a velocidade de difusão de um gás é inversamente proporcional à raiz quadrada de sua densidade e à raiz quadrada de sua massa molecular.
A efusão é a passagem de um gás através de um orifício. Graham relatou em 1846 que a velocidade de efusão de um gás através de um determinado orifício é inversamente proporcional à raiz quadrada de sua densidade ou de sua massa molecular. Este tornou-se o enunciado da Lei de Efusão de Graham.
Estes conceitos permitirão realizar cálculos com dados obtidos experimentalmente e compará-los com valores teóricos ou tabelados, e ainda demonstrar as leis dos gases.
Nota: As questões propostas no guia do experimento serão respondidas na discussão individual de cada experimento, de modo a inseri-las no contexto da explicação.
Parte Experimental
Parte I - Lei dos Gases e Misturas Gasosas
Material Utilizado
Béquer de volumes variados, pipeta, bureta, fita de magnésio, HCl 6mol/L, água destilada, lixa, rolha, fio de cobre, termômetro, cilindro graduado.
Procedimento e Observação
Pipetou-se 5ml de água destilada, e gotejou-se o líquido para dentro de uma bureta de 50ml afixada num suporte, de modo que somente sua parte não calibrada fosse completada com água. O resultado achado foi de 3,9ml, que chamaremos de VB.
Lixou-se uma fita de magnésio, de modo a eliminar os vestígios de impurezas e óxido em sua superfície. Pesou-se a fita brilhante e obteve-se 0,043g.
Usou-se em seguida uma rolha preparada, que consiste na rolha com um furo, através do qual se introduziu o fio de cobre de aproximadamente 10cm de comprimento, fixando-se este na rola com um pouco de fita adesiva. A fita de magnésio foi presa nesse fio de cobre, na parte que fica dentro do recipiente ao tampá-lo com a rolha.
Com auxílio da proveta, recolheu-se 15ml de HCl 6mol/litro e colocou-se este ácido na bureta, completando seu volume até a borda com água destilada. A bureta foi então tampada com a rolha preparada, de modo que a fita de magnésio fique na parte de dentro. A bureta foi então invertida e imediatamente mergulhada num béquer de 500ml com água até 3/4 do seu volume. Prendeu-se a bureta no suporte e iniciou-se a observação.
O ácido clorídrico, sendo mais denso que a água, fica inicialmente no fundo da bureta. Ao se inverter o tubo, percebe-se a descida do ácido, pela alteração gradual de densidade do líquido na bureta. Ao entrar em contato com a fita de magnésio, algumas bolhas começam a se formar. Com o tempo, mais ácido desce em direção ao magnésio, e mais bolhas se formam, indo para cima da bureta. Após alguns minutos, a fita de magnésio desaparece completamente (o fio de cobre não aparenta ser atacado pelo ácido, não influenciando na reação). A formação do gás na parte de cima da bureta empurra a coluna de líquido para baixo, e esta por sua vez sai da bureta, através do orifício na rolha.
Após a reação se completar, moveu-se a bureta para cima, de modo que o nível de líquido desta coincidisse com a superfície de líquido do béquer. Entretanto, com o material usado neste experimento, esse alinhamento não foi possível. A coluna de líquido da bureta permaneceu acima da superfície de líquido no béquer. Mediu-se assim mesmo o volume de gás no interior da bureta, tomando-se a escala graduada da bureta e adicionando a parte não graduada medida anteriormente. A parte graduada mostrou ser 38,9ml, que chamaremos de VA.
Mediu-se a temperatura de água do béquer, que por sua vez é igual à temperatura da água no interior da bureta, e que finalmente é igual à temperatura do gás hidrogênio formado. Esta foi de 22oC, ou 295K.
Analisemos na Discussão abaixo o restante dos cálculos efetuados.
Discussão
A reação utilizada é a seguinte:
Mg + 2HCl à MgCl2 + H2
Após a reação, o que resta na bureta é uma solução de cloreto de magnésio e ainda gás hidrogênio, que se acumula na parte superior. O objetivo é medir o volume de gás hidrogênio na reação e compará-lo com o previsto pela teoria.
Para isso, tomamos o volume final do gás gerado, que foi de 42,8ml, número este obtido da soma das leituras da parte calibrada e da parte não calibrada na bureta.
Para o cálculo do valor teórico, precisa-se da temperatura da reação em Kelvin, da pressão do gás hidrogênio no interior da bureta, além das medidas de massa do hidrogênio e magnésio (obtidas da Tabela Periódica). Vejamos como isso foi feito.
Ao nivelar o líquido da bureta com a superfície de água do béquer, faz-se com que a pressão exercida pela atmosfera sobre a água do béquer seja igual à pressão que a coluna de líquido na bureta exerce sobre o gás contido nesta. Não havendo esse alinhamento, a coluna de líquido tende a cair devido a seu próprio peso, ou subir, devido à pressão exercida pela água do béquer. Isso provocaria alteração na pressão do gás coletado no interior da bureta. Infelizmente o material utilizado no experimento não permite esse alinhamento dos níveis de líquido, portanto desde já sabe-se que a pressão medida do hidrogênio contém erro. Ainda assim, trabalharemos com esta medida, que foi de V=42,8ml.
Este gás hidrogênio na bureta não está puro, entretanto. Quando a água líquida entra em contato com um gás seco, um pouco de água evapora. Dessa forma, moléculas de água deixa o líquido e misturam-se com o gás seco. Esse fenômeno acontece até que a pressão parcial de vapor de água atinja um valor máximo. Chama-se esse valor de pressão de vapor de água. Este valor depende unicamente da temperatura, e não do gás usado, do volume do recipiente ou da pressão do gás. Assim sendo, o gás recolhido na bureta é uma mistura de H2 e H2O gasoso, pois o hidrogênio está em contato com a solução abaixo dele. Usando-se a Lei de Dalton, que determina que a pressão total é a soma da pressão parcial de H2 e vapor de água, além do valor experimental da pressão de vapor de água sob a temperatura medida, é possível então calcular a pressão do hidrogênio.
Tomando-se a pressão da bureta como sendo a pressão atmosférica, temos PB=760mmHg. A pressão parcial de vapor de água, a 22oC, é de aproximadamente 17,5mmHg (para 25oC, ela seria de 23,76mmHg). Então, PB= 760 = PH2 + 17,5. Logo, PH2 é igual a 742,5mmHg (menor que a pressão atmosférica, portanto).
Usamos agora do cálculo estequiométrico para deduzir a quantidade de matéria de gás hidrogênio produzida, levando em conta a quantidade de magnésio pesado. Assim, para 1 mol de magnésio que tem massa 24,3g, são produzidos 2g de hidrogênio. Para 0,043g determinadas na balança, a regra de três fornece 3,539 x 10-3 g de hidrogênio produzidos.
Pode-se agora usar a equação dos gases (PV=nRT) a fim de calcular o volume teórico de hidrogênio que se deveria obter no experimento. Assim,
PV = nRT <=> PV = (m/MM)RT
742,5 . V = (3,539 . 10-3/2) . 62,3 . 295
V = 0,0438 L => 43,8 mL
Esse valor teórico de 43,8ml representa um erro de 2,29% para o valor medido no experimento, que foi de 42,8ml. Uma precisão bastante razoável para os objetivos propostos.
Quais as possíveis causas de desvios entre os valores calculados teoricamente e o obtido experimentalmente? A precisão das medidas tomadas pode causar desvios, principalmente as medições de temperatura e volume, feitas observando-se escalas a olho nu. A massa de magnésio usada é relativamente precisa, tendo em vista o instrumental utilizado. O alinhamento incorreto da bureta com a superfície de líquido do béquer causou variação no volume medido de H2, e possivelmente agentes externos, como impurezas nos reagentes, podem influenciar na reação, alterando as quantidades resultantes de produtos.
Ainda, a pressão atmosférica no laboratório pode não ser precisamente 760mmHg, mas este foi o valor usado. E por fim, os cálculos usados no experimento (como a Lei de Dalton) levam em conta gases ideais, enquanto que se trabalhou com gases reais.
Parte II - Lei de Difusão de Graham
Material Utilizado
Tubo de vidro, suporte, chumaços de algodão, rolhas, cronômetro, régua, NH3 e HCl concentrados, béquer para recolher estas substâncias.
Procedimento e Observação
O tubo de vidro é montado no suporte, de modo que fique na posição horizontal. Embebeu-se um chumaço de algodão em HCl e outro em NH3, sendo que estes chumaços foram antes fixados nas rolhas. Imediatamente tampou-se o tubo com as rolhas, de modo que os chumaços ficassem para dentro do tubo. O cronômetro foi acionado e observou-se.
Vapores de gás começaram a se formar nos dois chumaços de algodão. Após cerca de um minuto, uma aura ou anel branco formou-se próximo ao HCl, quando então o cronômetro foi interrompido e sua medição anotada. Tomou-se a régua e anotou-se também as distâncias entre a aura e o chumaço de HCl e o chumaço de NH3. Após lavagem e secagem do tubo e rolhas, repetiu-se o experimento mais duas vezes. Os resultados estão demonstrados na Tabela 1.
De posse do tempo de cronômetro e distâncias percorridas por cada gás, calculou-se a velocidade difusão de cada gás no ar atmosférico dentro do tubo. Tomou-se então a média aritmética dessas velocidades, e aplicou-se a Lei de Graham para chegar ao número de razão. Vislumbremos esses cálculos na seção seguinte.
Discussão
A Lei ampliada de Graham pode ser aplicada de modo a se comparar as razões entre velocidades de difusão e pesos moleculares de dois gases distintos. A razão entre as velocidades de difusão dos dois gases é igual a raiz do inverso da razão entre os pesos moleculares dos dois gases. Ou seja,
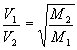 , onde V1 e V2 são as velocidades de difusão dos gases, e M1 e M2 seus pesos moleculares.
, onde V1 e V2 são as velocidades de difusão dos gases, e M1 e M2 seus pesos moleculares.
A Tabela 1 mostra os dados coletados nos três experimentos realizados. A Tabela 2 traz a média aritmética das velocidades de difusão encontradas, bem como os pesos moleculares dos gases, calculados conforme valores da tabela periódica.
Experimento 1 | Experimento 2 | Experimento 3 | ||||
HCl | NH3 | HCl | NH3 | HCl | NH3 | |
Tempo Cronômetro (segundos) | 68’ | 66’ | 76’ | |||
Distância percorrida (cm) | 12,0 | 16,0 | 11,5 | 16,5 | 10,5 | 17,5 |
Velocidade (cm/s) | 0,1764 | 0,2353 | 0,1742 | 0,2500 | 0,1382 | 0,2303 |
HCl | NH3 | |
Velocidade Média Experimental (cm/s) | 0,1629 | 0,2385 |
Peso Molecular (Tabela Periódica) | 36,5u.m.a. | 17u.m.a. |
Usemos agora dos valores para calcular a razão entre as velocidades de difusão no ar atmosférico e os pesos moleculares respectivos dos gases.
![]()
![]()
![]()
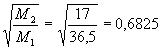
Desta forma, obtivemos uma razão experimental entre as velocidades de 0,6830, enquanto que a teoria dá a razão entre o inverso das raízes das massas moleculares de 0,6825. Um surpreendente erro de 0,0005 ou 0,07%.
Vejamos agora no Gráfico 1 velocidades de reação de alguns gases versus seu peso molecular. Os dados do HCl e do NH3 foram os obtidos neste experimento. Os pontos são plotados na sequência em que os gases são mostrados na tabela, ou seja, o primeiro ponto corresponde ao H2, o segundo ao He e assim por diante.
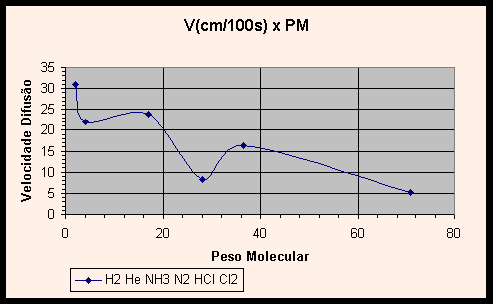 |
Percebe-se que as velocidades de difusão tendem a cair com o aumento do peso molecular.
Verifiquemos agora o Gráfico 2, log x log, com os mesmos dados. (Veja explicações detalhadas sobre os gráficos no Anexo A.)
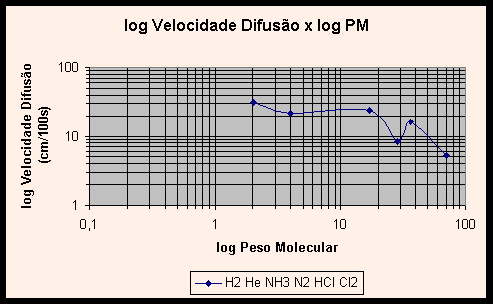 |
Tomando dois pontos distintos neste gráfico, podemos calcular o coeficiente logarítmico entre os valores. Assim, usando as velocidades e pesos do hidrogênio e hélio, temos:
![]() , onde V=k . PMn .
, onde V=k . PMn .
O coeficiente de –0,494 indica que a relação entre V e PM é que V é igual ao inverso da raiz de PM, se aproximamos o valor achado para –0,5, que indica inverso da raiz quadrada. Comprova-se, assim, a relação indicada pela Lei de Graham.
Conclusão
Os experimentos realizados puderam confirmar vários itens teóricos no estudo de gases em Química. Pode-se tomar medidas experimentais, efetuar cálculos com elas, e comparar a dados achados na teoria. Os dados obtidos nos experimentos ficaram muito próximos dos teóricos, o que dá extrema validade aos experimentos realizados e serve de base irrefutável aos conceitos aprendidos.
O volume de gás hidrogênio obtido no experimento 1 apresentou erro de 2,29% do valor esperado teoricamente. Um erro muito pequeno, levando em conta as condições do experimento, e comprova que a equação dos gases, e a combinação das leis de Charles, Boyle, o princípio de Avogadro e a Lei de Dalton podem ser observadas numa experimentação simples.
Por outro lado, os valores obtidos no experimento 2 mostrou um erro surpreendentemente pequeno, de apenas 0,07%, se comparado aos valores teóricos ou obtidos segundo experimentos extremamente precisos. Assim, tabelando e efetuando comparações e cálculos com os dados, pôde-se chegar à mesma conclusão que Thomas Graham chegou no século 19: a velocidade de difusão de um gás através de outro é inversamente proporcional à raiz quadrada de sua massa molecular.
Bibliografia
Russel, John Blair. (1994) Química Geral; vol. I, 2. Edição; Makron Books, São Paulo; p. 140 a 177.
Brady, James E. - Humiston, Gerard E. (1996). Química Geral; vol. I, 2. Edição; Ed. Moderna Ltda., São Paulo; p.225 a 254.
Microsoft Encarta 97 Encyclopedia, (1996)
Copyright 1993-1996, Microsoft Corporation (
Vislumbrando os gráficos (1) V x PM e (2) log V x log PM dos gases, nota-se uma curva não característica, que não ilustra apropriadamente a relação entre velocidade de difusão e peso molecular. Na verdade, a inclusão dos valores experimentais obtidos para HCl e NH3 e aqui relatados distorcem os gráficos. Com efeito, se adicionarmos uma linha de tendência a cada gráfico, verifica-se que o gráfico V x PM tem uma curva no formato potência decrescente, e o gráfico linearizado log V x log PM apresenta a esperada reta.
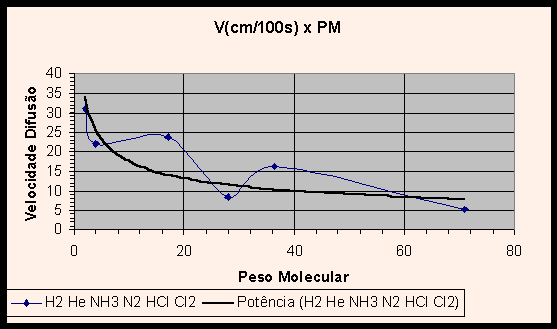 |
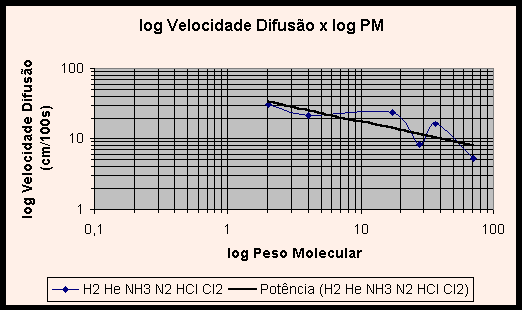 |
Essas linhas de tendência ilustram com propriedade a relação entre velocidade de difusão e o inverso da raiz do peso molecular. A pergunta que suscita é: por que a inclusão dos valores obtidos em nossos experimentos distorce os gráficos tão violentamente, se o erro experimental encontrado foi de 0,07%? Não deveriam os valores obtidos ajustarem-se às curvas do gráfico, e não distorcê-lo?
A razão de tal incongruência é que, de fato, o erro experimental da razão entre as velocidades de difusão do HCl e NH3 foi pequeno, entretanto os valores individuais das velocidades de difusão obtidos no experimento contém grande erro. Como as duas grandezas foram divididas, estes erros individuais foram mascarados ou quase totalmente eliminados, dando lugar a uma razão próxima à teórica. Como nos gráficos os valores são tomados individualmente, os erros agora aparecem de forma clara, provocando a distorção no gráfico e produzindo as curvas pitorescas apresentadas nos gráficos 1 e 2, ao invés das esperadas linhas de potência decrescente e reta.
Isso pode ser melhor entendido da seguinte forma. Tomando-se duas medidas, 2 e 1, obtemos como razão entre as mesmas 2/1=2. Toma-se agora duas outras medidas, 2000 e 1000, a razão entre elas é precisamente 2, idêntica à razão das duas primeiras medidas. Entretanto, os valores individuais dos pares de medidas são completamente diferentes, na ordem de 1000 vezes maior. Se hipoteticamente essas fossem as medidas de velocidade de dois gases, sendo o primeiro par a medida real, e o segundo par a medida experimental, encontrar-se-ia precisamente a mesma razão entre as velocidades. Entretanto, o erro individual de cada medida seria absurdo.
Assim, prova-se que o experimento, apesar de extremamente válido, ainda contém muito erro, como falhas na leitura do cronômetro, atraso no seu acionamento ou parada, falhas na medição de distâncias percorridas do gás e impurezas no gás ou tubo.
De qualquer forma, como a relação expandida de Graham supõe razões, ela pode ser aplicada em ambos os casos e chegar-se-á a valores próximos, se os erros individuais de cada gás forem semelhantes.