Eliminação Gaussiana
Projeto para Matlab
Rafael G. B. Araújo
Antônia F. Cruz
Albert R. Moreira
Marcos Portnoi
Engenharia Elétrica 2./Mat – UNIFACS
22.Junho.2000
http://surf.to/locksmith
"O medo de quem navega é a terra."
--
Amyr Klink Objetivos *Introdução *Programa *gelim.m *inputaug.m *pivot.m *Resolução dos Problemas Propostos *
Problema 1 *Problema 2 *Conclusão *Referência *
Confeccionar um programa para o aplicativo Matlab, implementando a eliminação gaussiana para qualquer matriz aumentada, advinda de um sistema de equações, fornecida. A matriz resultante deve ser uma matriz triangular superior, e o programa também deve realizar retrosubstituição de modo a calcular os valores das variáveis do sistema.
O aplicativo Matlab possui uma linguagem procedural própria, o que permite a confecção de programas para ser nele executados e também funções extras. Esses programas e funções são arquivos texto que recebem a extensão .m. O Matlab versão 5.3 já possui funções internas para redução de uma matriz a seu formato unitário (row reduced echelon form), usando eliminação do tipo Gauss-Jordan com pivoteamento parcial, e também possui funções para resolução de sistemas de equações. De modo prático, a confecção de um programa para resolução de sistemas pelo método de Gauss seria desnecessária no Matlab, mas o objetivo didático é usar da linguagem disponível para a programação de um algoritmo de cálculo numérico.
Dessa maneira, os programas aqui confeccionados usam de métodos inteiramente procedurais para atingir seus resultados, mesmo que o Matlab possua recursos poderosos que poderiam porventura simplificar o algoritmo. De fato, o Matlab manuseia matrizes com extrema facilidade, tornando a troca de linhas dentro de uma matriz, ou a multiplicação de uma linha por um coeficiente, ou mesmo a procura de um elemento de maior valor dentro de uma coluna, uma operação simples de apenas um comando. Novamente, o enfoque deste projeto foi completamente procedural, realizando as operações elemento a elemento, como seria feito pela linguagem C.
Um exemplo do poder de manipulação de matrizes do Matlab é visto na listagem da função interna rref (pode-se obter essa listagem digitando open rref no workspace), que é a função de redução de uma matriz pelo método Gauss-Jordan.
A eliminação gaussiana consiste em realizar n-1 eliminações (onde n é o número de linhas da matriz), usando do procedimento abaixo:
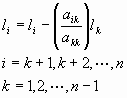
Equação 1: Fórmula de Gauss
Dois problemas envolvendo treliças serão então resolvidos usando do programa confeccionado.
Este é o programa principal. O uso consiste em digitar gelim no workspace. O programa solicitará a entrada da matriz no formato Matlab. Somente matrizes aumentadas e não nulas e não vazias são aceitas. Após a entrada, o programa iniciará a eliminação gaussiana, primeiramente pivoteando a matriz a cada eliminação (de modo a que o elemento pivô seja sempre o elemento de maior valor absoluto dentro da coluna, de cima para baixo), e então perfazendo a substituição de linhas usando a fórmula de Gauss (Equação 1).
Ao final, o programa mostra a matriz triangular superior resultante e os valores das variáveis do sistema. Em caso de sistemas indeterminados ou impossíveis, a matriz triangular é mostrada e as variáveis serão representadas por infinitos ou NaN’s (Not a Number, a representação matemática padronizada para ocorrências do tipo 0 = 0).
%GELIM Triangularização de matrizes por eliminação gaussiana. % % Este programa calcula a matriz triangularizada a partir da matriz aumentada, % usando eliminação gaussiana. % Fornece também os valores das variáveis de sistema representados % na matriz aumentada. % % Em caso de sistema indefinido ou impossível, a matriz triangularizada é mostrada % e as variáveis do sistema serão representadas por infinitos ou NaN's (0=0). % % Saídas: a (matriz triangularizada) % x (vetor das variáveis do sistema) % % Veja também PIVOT, INPUTAUG. % % por Marcos Portnoi, 06/2000 última alteração 25/06/2000 13:15 % % clear all warning off %desabilita msg warning em caso de divisão por zero em sistemas impossíveis ou indeterminadosdummy=0; disp( ' ')disp( ' ')disp( 'Este programa calcula a matriz triangularizada a partir da matriz aumentada,')disp( 'usando eliminação gaussiana.')disp( 'Fornece também os valores das variáveis de sistema representados')disp( 'na matriz aumentada.')disp( ' ')disp( 'Em caso de um sistema indefinido, a matriz triangularizada será calculada')disp( 'e os valores das variáveis do sistema serão representadas por infinitos.')disp( ' ')[a,r,c]=inputaug(dummy); %nenhum argumento é transmitido à funçãofor i=2:r %primeiro loop, controla numero de eliminacoes = número de linhas-1[a,f]=pivot(a,i,r,c);if f==0 %se flag f = 1, pivô é nulo; passar para coluna seguinte (toda a coluna abaixo já é nula)for j=i:r %da linha atual até a última%cada eliminação deve ser feita da linha corrente até a última m=a(j,i-1)/a(i-1,i-1); %multiplicadora(j,i-1)=0; %faz elemento igual a zero (eliminacao gaussiana), evitando aproximacoes pela divisãofor k=i:c %do elemento linha até o último elemento (coluna) da linha atuala(j,k)=a(j,k)-m*a(i-1,k); %formula de Gaussend %next kend %next jend %endif end %next i
%Retrosubstituição procedural x(r)=a(r,c)/a(r,c-1); %primeira substituicaofor i=r-1:-1:1 %linha da retrosubstituicaox(i)=a(i,c); for j=c-1:-1:i+1 %coluna da retrosubstituicaox(i)=x(i)-a(i,j)*x(j);endx(i)=x(i)/a(i,i);end %Mostrar resultados disp( ' ')disp( 'Matriz triangularizada:')a disp( 'Valores das variaveis do sistema:')x warning backtrace %reabilita msg warning
|
Programa 1: gelim.m
Função que solicita a entrada da matriz pelo usuário e testa para matrizes nulas ou vazias. Nenhum argumento precisa ser passado para a função, mas ele está presente devido à sintaxe obrigatória.
function [a,r,c] = inputaug(dummy)%INPUTAUG(dummy) Solicita entrada de uma matriz pelo usuário. % [a,r,c]=INPUTAUG(dummy) solicita a entrada de uma matriz pelo teclado, % no formato Matlab apropriado. Apenas matrizes não-nulas, não vazias e % aumentadas são aceitas. O argumento 'dummy' não é utilizado pela função % e apenas garante a sintaxe. % % INPUTAUG retorna os seguintes valores: % % a matriz aumentada % r número de linhas (rows) da matriz aumentada % c número de colunas (columns) da matriz aumentada (sempre r+1) % % Veja também GELIM, PIVOT. % % por Marcos Portnoi, 06/2000 última alteração 25/06/2000 13:17 % % r=0; %numero de linhas da matrizc=0; %numero de colunas da matriza=1; %matriz aumentadawhile (isempty(a)) | (c<r+1)a=input( 'Entre com a matriz aumentada no formato Matlab apropriado\n: ')[r,c]=size(a); if isempty(a)disp( 'Erro: matriz nula ou vazia.')endif c<r+1 %número de colunas é igual a número de linhas + 1?disp('Erro: matriz nao aumentada.')endend %return |
Função 1: inputaug.m
Esta função realiza o pivoteamento da matriz, da linha atual até a última, procurando o elemento na coluna apropriada de maior valor absoluto. Uma vez encontrado, a linha atual é trocada pela linha com o elemento de maior valor absoluto encontrado, mesmo que seja a mesma linha (quando então nada mudará). Se o elemento ou pivô resultante for nulo, então nenhuma eliminação necessita ser executada, e a função retorna uma flag ativada para o programa.
O pivoteamento é importante a fim de evitar pivôs nulos (e subsequente divisão por zero) e também reduz os erros de arredondamento.
Verifique-se, no início do programa, um algoritmo de pivoteamento usando de recursos de manipulação de matrizes do Matlab. Esse algoritmo está desativado (comentado), para que somente a parte procedural funcione.
function [a,f] = pivot(a,i,r,c)%PIVOT Função de pivoteamento de matrizes % [a,f] = PIVOT(a,i,r,c) realiza o pivoteamento de uma matriz para uso % da eliminação gaussiana, evitando pivôs nulos e diminuindo % erros de arredondamento. PIVOT verifica o elemento da coluna pivô % com maior valor absoluto, desconsiderando as linhas anteriores, % e troca a linha corrente pela linha com este elemento de maior valor % absoluto encontrado. % A eliminação gaussiana prevê matrizes aumentadas, mas a função PIVOT % funciona com matrizes de qualquer dimensão. % % Os argumentos a serem passados são: % % a matriz a ser pivoteada % i linha corrente ou atual, abaixo da qual os elementos serão testados % r número de linhas (rows) da matriz % c número de colunas (columns) da matriz % % A função retorna: % % a matriz pivoteada % f flag (1 = pivô nulo, 0 = pivô não nulo) % % Veja também GELIM, INPUTAUG. % % por Marcos Portnoi, 06/2000 última alteração 25/06/2000 17:01 % % f=0; %flag = 1 para pivô nulo%Processo abaixo usa poder de manipulação de matrizes do Matlab %p=i-1; %[p,p]=max(abs(a(i-1:r,i-1))); %acha índice da linha com maior valor absoluto na coluna atual para baixo %p=p+(i-1)-1; %ajusta valor de p, que antes era relativo à linha atual %Troca linha p por linha i-1 %a([i-1 p],:)=a([p i-1],:); %Método abaixo é completamente procedural p=i-1; for j=i:r %testar qual elemento na coluna atual tem o maior valor absolutoif abs(a(i-1,i-1))<abs(a(j,i-1)) %da linha atual até a últimap=j; %se modulo elemento testado for maior, faça sua linha a pivôendend %variavel p contém a linha com elemento de maior valor absoluto, ou linha do elemento pivot %inicia processo de troca de linhas, elemento por elemento for j=1:caux=a(i-1,j); a(i-1,j)=a(p,j); a(p,j)=aux; end if a(i-1,i-1)==0 %se pivô for nulo, setar flagf=1;end %return |
Função 2: pivot.m
Resolução dos Problemas Propostos
Seja a treliça abaixo:
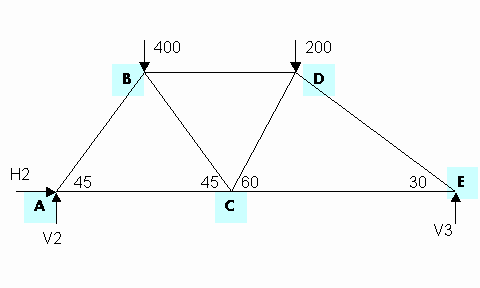
Figura 1: treliça e forças atuantes
O sistema de forças atuantes na treliça, compreendendo as reações nos vértices A e E, as cargas e as forças de compressão e tensão das vigas, é representado conforme segue:
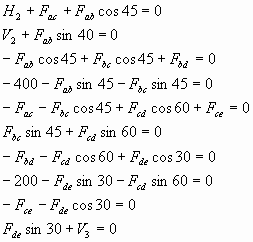
Sistema 1
O sistema é colocado sob a forma de matriz e alimentado ao programa gelim.m, o qual fornece o seguinte resultado:
Output Questão 4:
» gelim
Este programa calcula a matriz triangularizada a partir da matriz aumentada, usando eliminação gaussiana. Fornece também os valores das variáveis de sistema representados na matriz aumentada.
Em caso de um sistema indefinido, a matriz triangularizada será calculada e os valores das variáveis do sistema serão representadas por infinitos.
Entre com a matriz aumentada no formato Matlab apropriado : [0 0 1 .707 1 0 0 0 0 0 0; 1 0 0 .707 0 0 0 0 0 0 0; 0 0 0 -.707 0 .707 1 0 0 0 0; 0 0 0 -.707 0 -.707 0 0 0 0 400; 0 0 0 0 -1 -.707 0 .5 1 0 0; 0 0 0 0 0 .707 0 .87 0 0 0; 0 0 0 0 0 0 -1 -.5 0 .87 0; 0 0 0 0 0 0 0 -.87 0 -.5 200; 0 0 0 0 0 0 0 0 -1 -.87 0; 0 1 0 0 0 0 0 0 0 .5 0]
a =
Columns 1 through 6
0 0 1 0.707 1 0 1 0 0 0.707 0 0 0 0 0 -0.707 0 0.707 0 0 0 -0.707 0 -0.707 0 0 0 0 -1 -0.707 0 0 0 0 0 0.707 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0
Columns 7 through 11
0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 400 0 0.5 1 0 0 0 0.87 0 0 0 -1 -0.5 0 0.87 0 0 -0.87 0 -0.5 200 0 0 -1 -0.87 0 0 0 0 0.5 0
Matriz triangularizada:
a =
Columns 1 through 6
1 0 0 0.707 0 0 0 1 0 0 0 0 0 0 1 0.707 1 0 0 0 0 -0.707 0 -0.707 0 0 0 0 -1 -0.707 0 0 0 0 0 1.414 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Columns 7 through 11
0 0 0 0 0 0 0 0 0.5 0 0 0 0 0 0 0 0 0 0 400 0 0.5 1 0 0 1 0 0 0 -400 -1 -0.5 0 0.87 0 0 1.12 0 -0.435 200 0 0 -1 -0.87 0 0 0 0 -0.8379 355.36
Valores das variaveis do sistema:
x =
Columns 1 through 6
387.95 212.05 5.6843e-014 -548.72 387.95 -17.046
Columns 7 through 10
-375.9 13.853 368.97 -424.1
» |
Output problema 1
Ou seja, as forças têm os seguintes valores (de acordo com a ordem de colocação na matriz), em valores absolutos:
|
|
Solução sistema 1
Observe que V2+V3 é igual ao somatório das cargas aplicadas à treliça.
Seja a treliça abaixo:
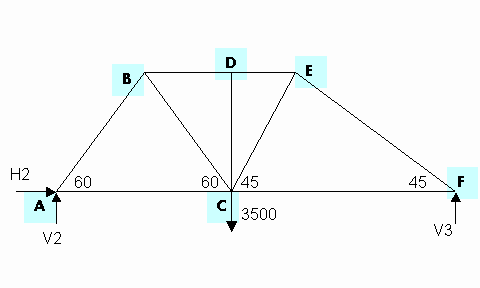
Figura 2: treliça e forças atuantes
.O sistema de forças atuantes na treliça, compreendendo as reações nos vértices A e F, a carga e as forças de compressão e tensão das vigas, é representado conforme segue:
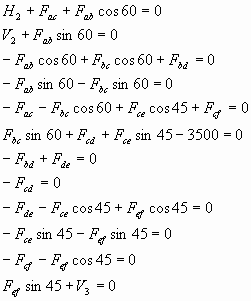
Sistema 2
O sistema é novamente colocado sob a forma de matriz e alimentado ao programa gelim.m, o qual fornece o seguinte resultado:
Output Questão 5:
» gelim
Este programa calcula a matriz triangularizada a partir da matriz aumentada, usando eliminação gaussiana. Fornece também os valores das variáveis de sistema representados na matriz aumentada.
Em caso de um sistema indefinido, a matriz triangularizada será calculada e os valores das variáveis do sistema serão representadas por infinitos.
Entre com a matriz aumentada no formato Matlab apropriado : [1 0 0 .5 1 0 0 0 0 0 0 0 0; 0 1 0 .866 0 0 0 0 0 0 0 0 0; 0 0 0 -.5 0 .5 1 0 0 0 0 0 0; 0 0 0 -.866 0 -.866 0 0 0 0 0 0 0; 0 0 0 0 -1 -.5 0 0 .707 1 0 0 0; 0 0 0 0 0 .866 0 1 .707 0 0 0 3500; 0 0 0 0 0 0 -1 0 0 0 1 0 0; 0 0 0 0 0 0 0 -1 0 0 0 0 0; 0 0 0 0 0 0 0 0 -.707 0 -1 .707 0; 0 0 0 0 0 0 0 0 -.707 0 0 -.707 0; 0 0 0 0 0 0 0 0 0 -1 0 -.707 0; 0 0 1 0 0 0 0 0 0 0 0 .707 0]
a =
Columns 1 through 6
1 0 0 0.5 1 0 0 1 0 0.866 0 0 0 0 0 -0.5 0 0.5 0 0 0 -0.866 0 -0.866 0 0 0 0 -1 -0.5 0 0 0 0 0 0.866 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0
Columns 7 through 12
0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0.707 1 0 0 0 1 0.707 0 0 0 -1 0 0 0 1 0 0 -1 0 0 0 0 0 0 -0.707 0 -1 0.707 0 0 -0.707 0 0 -0.707 0 0 0 -1 0 -0.707 0 0 0 0 0 0.707
Column 13
0 0 0 0 0 3500 0 0 0 0 0 0
Matriz triangularizada:
a =
Columns 1 through 6
1 0 0 0.5 1 0 0 1 0 0.866 0 0 0 0 1 0 0 0 0 0 0 -0.866 0 -0.866 0 0 0 0 -1 -0.5 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Columns 7 through 12
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.707 0 0 0 0 0 0 0 0 0.707 1 0 0 1 0 0 0 0 0 -1 0 0 0 1 0 0 -1 0 0 0 0 0 0 -0.707 0 -1 0.707 0 0 0 -1 0 -0.707 0 0 0 0 -1.866 0.707 0 0 0 0 0 -1.0351
Column 13
0 0 0 0 0 0 0 0 0 0 3500 1875.7
Valores das variaveis do sistema:
x =
Columns 1 through 6
0 2218.9 1281.1 -2562.2 1281.1 2562.2
Columns 7 through 12
-2562.2 0 1812 1281.1 -2562.2 -1812
» |
Output problema 2
Por conseguinte, as forças têm os seguintes valores (de acordo com a ordem de colocação na matriz), em valores absolutos:
|
|
Solução sistema 2
Observar que, como esperado, V2+V3 é igual à carga aplicada à treliça.
O projeto permite comprovar a eficácia do método de eliminação gaussiana na resolução de sistemas. Sobretudo significa facilitação da resolução de um sistema de muitas equações, a exemplo dos sistemas de treliças, representados por 10 ou mais equações, aliado a uma ferramenta para automação dos cálculos como o Matlab ou mesmo a linguagem C, sem a qual as eliminações tornar-se-iam muito laboriosas.
Em adição, verifica-se que o método de eliminação gaussiana é implementado de forma simples através de um programa ou algoritmo.
BEER, Ferdinand P.; JOHNSTON Jr., E. Russel (1994) Mecânica Vetorial para Engenheiros: Estática; vol. I, 5. Edição; Makron Books do Brasil Editora Ltda., São Paulo, SP; p. 369 a 385.