![]()
(1)
PERDA DE CARGA EM FLUIDOS INCOMPRESSÍVEIS
RELATÓRIO DE EXPERIMENTOS
Marcos Portnoi
Influência da Vazão Sobre a Perda de Carga
Este relatório pretende descrever experimentos realizados com água percorrendo um sistema de tubos de PVC. Com medições de pressão, objetiva-se: (a) verificar a influência do diâmetro do tubo sobre a perda de carga, (b) verificar a influência da vazão sobre a perda de carga, (c) calcular a rugosidade do PVC e comparar com o valor tabelado e (d) discutir os resultados obtidos de acordo com os conceitos teóricos de escoamento dos fluidos.
O sistema usado para estudos e experimentos de perda de carga em escoamento de fluidos incompressíveis consistiu em um tanque de água, uma bomba de circulação de água e quatro opções de tubulações, com diâmetros nominais ½", ¾", 1" e 1 ½". A vazão é medida através de um rotâmetro em LPM (litros por minuto). A medição da perda de carga nos trechos de tubulação é feita através de um tubo em "U" invertido, para coleta das diferenças de pressão.
A perda de carga, basicamente, consiste em uma perda energética no escoamento, que aparece como uma diminuição da pressão no escoamento a jusante. A energia dissipada pode converter-se em calor para o próprio fluido.
Esta perda de carga, chamada hL, é relacionada na equação de Bernoulli da seguinte forma:
| (1) |
A perda de carga pode ser calculada segundo diferença de pressões, se a altura e velocidades do escoamento em 1 e 2 forem iguais.
| (2) |
A perda de carga é função do comprimento do duto, da rugosidade do material que compõe o duto, da velocidade do escoamento, do diâmetro do duto e do tipo do escoamento. Para o escoamento laminar,
| (3) |
onde L é o comprimento do tubo, D é o diâmetro, V é a velocidade do escoamento e Re é o número de Reynolds, conforme a equação abaixo.
| (4) |
onde D e V são as variáveis definidas acima, ρ é a massa específica e µ é a viscosidade do fluido. Para o escoamento turbulento, a perda de carga é:
| (5) |
Esta é a chamada Equação de Darcy, e o fator de fricção, f, por ela definido, é o Fator de Darcy. O fator de Darcy pode ser obtido no Diagrama de Moody ou ainda calculado analiticamente segundo a Equação de Colebrook:
| (6) |
onde ε é a rugosidade do tubo (motivo de cálculo dos experimentos aqui relatados).
Mediu-se os diâmetros internos dos quatro tubos, utilizando-se de um paquímetro e de pedaços dos mesmos tubos usados na montagem do aparato de experimentos.
Tubo ¾": 20,50mm
Tubo ½": 15,40mm
Tubo 1": 25,70mm
Tubo 1 ½": 38,4mm
À saída da bomba há um rotâmetro, ou medidor de vazão. Uma forma de calibrar-se este medidor consiste em marcar um tempo fixo (num cronômetro) e medir então a quantidade ou volume de água que sai da bomba. Uma outra forma é estipular um volume fixo e então medir o tempo que a bomba consome para completar tal volume de controle. As duas formas resultarão na vazão. Nenhum procedimento deste tipo foi tomado, entretanto, e tomou-se as medições de vazão conforme indicadas pelo rotâmetro.
Influência da Vazão Sobre a Perda de Carga
Conectou-se o tubo em "U" invertido no tubo de ¾". Para dez vazões diferentes, mediu-se as alturas de líquido no tubo em "U". A diferença de pressão entre os pontos 1, 2, 3 e 4 é obtida segundo o princípio da estática dos fluidos.
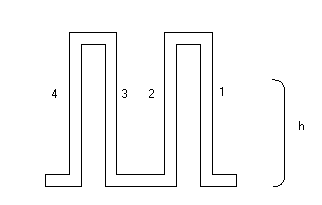
Ilustração 1: Tubo em "U" invertido para medição de pressões.
A coluna 1 é conectada a montante (entrada do escoamento) e a coluna 4 é conectada a jusante (saída do escoamento). Entre os tubos 2 e 3 há uma válvula para escape de fluido preso, ou ainda para alívio do acúmulo de ar. Desprezando-se a massa específica do ar, a equação usada para diferença de pressão entre os pontos de entrada em 1 (P1) e saída em 4 (P4) é:
| (7) |
O gráfico da perda de carga versus vazão está abaixo.
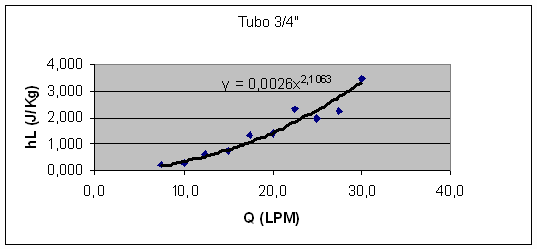
Ilustração 2: Gráfico para tubo de 3/4".
Vê-se que a curva é do tipo potência, com expoente de aproximadamente 2. Ou seja, a perda de carga varia com o quadrado da vazão. O gráfico log x log é:
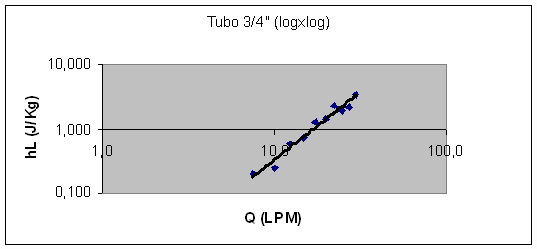
Ilustração 3: Gráfico logxlog para tubo de 3/4".
Observa-se que a reta para o gráfico logxlog é linear, com inclinação de aproximadamente 2. Isso é coerente com a Equação de Darcy, para o caso de f ser aproximadamente constante. No Diagrama de Moody, verifica-se que para a variação do número de Reynolds no experimento, o fator de Darcy varia em alguns pontos na potência de 10-4, o que pode ser considerado praticamente constante.
As Tabelas abaixo trazem os dados coletados para os quatros diâmetros de tubo.
Tubo 3/4" | 20,50 | mm | L=184cm | ||||
h1 (cm) | h2 (cm) | h3 (cm) | h4 (cm) | Vazão (LPM) | hL (J/Kg) | V (m/s) | Re |
28,5 | 0,0 | 0,0 | 26,5 | 7,5 | 0,196 | 0,38 | 7765 |
19,0 | 0,0 | 0,0 | 16,5 | 10,0 | 0,245 | 0,51 | 10354 |
15,5 | 0,0 | 0,0 | 9,5 | 12,5 | 0,588 | 0,63 | 12942 |
19,0 | 0,0 | 0,0 | 11,5 | 15,0 | 0,735 | 0,76 | 15531 |
40,0 | 0,0 | 0,0 | 26,5 | 17,5 | 1,323 | 0,88 | 18119 |
26,0 | 0,0 | 0,0 | 11,5 | 20,0 | 1,421 | 1,01 | 20708 |
57,0 | 0,0 | 0,0 | 33,5 | 22,5 | 2,303 | 1,14 | 23296 |
36,5 | 0,0 | 0,0 | 16,5 | 25,0 | 1,960 | 1,26 | 25885 |
61,5 | 0,0 | 0,0 | 38,5 | 27,5 | 2,254 | 1,39 | 28473 |
63,0 | 0,0 | 0,0 | 27,5 | 30,0 | 3,479 | 1,52 | 31062 |
Tabela 1: Dados coletados para tubo 3/4".
| Tubo 1" | 25,70 | mm | L=183,5cm | ||||
h1 (cm) | h2 (cm) | h3 (cm) | h4 (cm) | Vazão (LPM) | hL (J/Kg) | V (m/s) | Re |
46,0 | 0,0 | 0,0 | 35,5 | 30,0 | 1,029 | 0,96 | 24777 |
40,0 | 0,0 | 0,0 | 30,5 | 27,5 | 0,931 | 0,88 | 22712 |
25,5 | 0,0 | 0,0 | 20,0 | 25,0 | 0,539 | 0,80 | 20647 |
19,0 | 0,0 | 0,0 | 14,5 | 22,5 | 0,441 | 0,72 | 18583 |
16,5 | 0,0 | 0,0 | 12,5 | 20,0 | 0,392 | 0,64 | 16518 |
33,0 | 0,0 | 0,0 | 30,0 | 17,5 | 0,294 | 0,56 | 14453 |
32,0 | 0,0 | 0,0 | 29,0 | 15,0 | 0,294 | 0,48 | 12388 |
38,5 | 0,0 | 0,0 | 37,0 | 12,5 | 0,147 | 0,40 | 10324 |
36,0 | 0,0 | 0,0 | 35,0 | 10,0 | 0,098 | 0,32 | 8259 |
34,0 | 0,0 | 0,0 | 33,0 | 7,5 | 0,098 | 0,24 | 6194 |
Tabela 2: Dados coletados para tubo 1".
| Tubo 1/2" | 15,40 | mm | L=183,0cm | ||||
h1 (cm) | h2 (cm) | h3 (cm) | h4 (cm) | Vazão (LPM) | hL (J/Kg) | V (m/s) | Re |
32,0 | 0,0 | 0,0 | 29,5 | 7,0 | 0,245 | 0,63 | 9648 |
40,0 | 0,0 | 0,0 | 27,5 | 10,0 | 1,225 | 0,89 | 13783 |
40,0 | 0,0 | 0,0 | 28,0 | 15,0 | 1,176 | 1,34 | 20674 |
86,5 | 0,0 | 0,0 | 27,0 | 20,0 | 5,831 | 1,79 | 27566 |
101,0 | 2,5 | 20,0 | 21,0 | 21,0 | 9,555 | 1,88 | 28944 |
77,5 | 13,0 | 11,0 | 17,0 | 17,0 | 5,733 | 1,52 | 23431 |
64,0 | 19,2 | 6,8 | 10,5 | 10,5 | 4,028 | 0,94 | 14472 |
Tabela 3: Dados coletados para tubo 1/2".
| Tubo 1 1/2" | 38,40 | mm | L=182,5cm | ||||
h1 (cm) | h2 (cm) | h3 (cm) | h4 (cm) | Vazão (LPM) | hL (J/Kg) | V (m/s) | Re |
24,5 | 0,0 | 0,0 | 24,5 | 27,5 | 0,0 | 0,40 | 15201 |
50,0 | 0,0 | 0,0 | 50,0 | 30,0 | 0,0 | 0,43 | 16582 |
40,5 | 0,0 | 0,0 | 40,5 | 25,0 | 0,0 | 0,36 | 13819 |
Tabela 4: Dados coletados para tubo 1 1/2".
Vejamos os gráficos perda de carga versus vazão dos tubos 1" e ½".
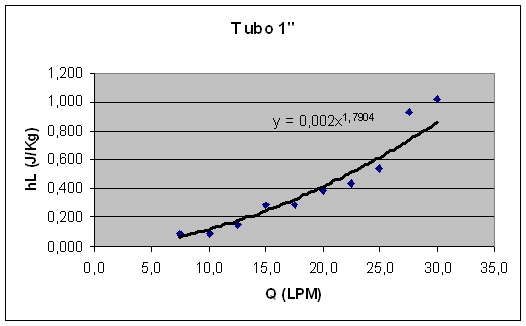
Ilustração 4: Perda de carga versus vazão para tubo 1".
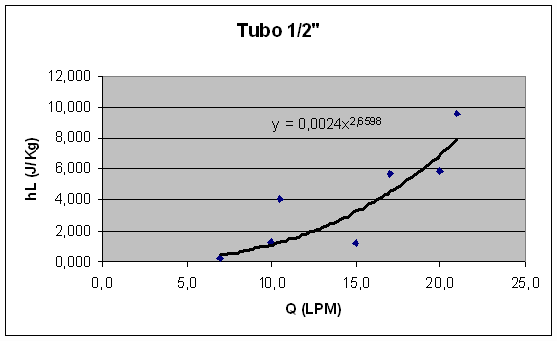
Ilustração 5: Perda de carga vesus vazão para tubo 1/2".
Verifica-se que, em vazões elevadas, apenas duas colunas de líquido para medição de pressão são insuficientes no caso do tubo de ½". Nestas vazões, as colunas rapidamente se enchem (sinal de alta pressão dentro do tubo) e não é possível realizar as medições. Toma-se então o sistema com quatro colunas de fluido. Entretanto, como pode-se observar no gráfico, os dados medidos apresentam dispersão mais evidente, o que resulta num expoente para a vazão de cerca de 2,7. Também a perda de carga é maior que para os outros tubos, o que é coerente com a equação de Darcy (a variável diâmetro está no denominador). Ainda, pela observação do número de Reynolds, o escoamento pelo tubo de ½" entra em níveis de turbulência mais elevados que os outros.
Observa-se, finalmente, que o tubo de 1 ½" não apresentou perda de carga. Isso não é coerente com a teoria, pois, mesmo que, devido ao maior diâmetro, este tubo mostrasse perdas de carga menores, elas ainda deveriam ser mensuráveis. A investigação mostrou ser esse problema resultado da montagem do sistema de tubos e do ponto de tomada de pressão. Como mostra a Ilustração 6, o fluido percorre tubos de diâmetro menor até entrarem no tubo de 1 ½". Logo no ponto de aumento de diâmetro, é feita a tomada de pressão.
Neste ponto, entretanto, o escoamento ainda não se desenvolveu completamente, e está ali sujeito a turbulência provocada pelo aumento súbito de diâmetro e cantos vivos. Este problema seria solucionado com o deslocamento do ponto de tomada de pressão mais a jusante do aumento de diâmetro.
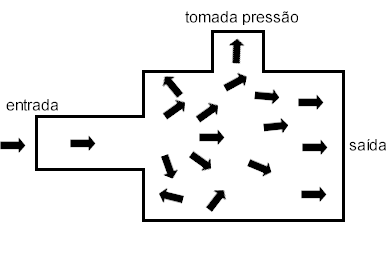
Ilustração 6: Tomada de pressão no tubo 1 1/2" (região de turbulência).
Influência do Diâmetro do Tubo sobre a Perda de Carga
O gráfico abaixo mostra a perda de carga máxima de cada tubo versus o diâmetro em metros.
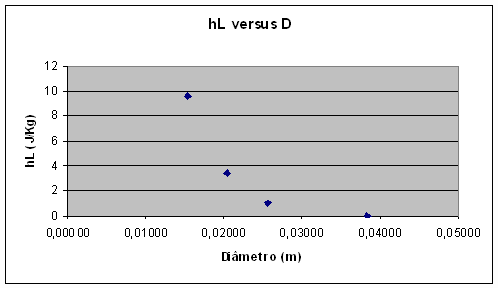
Ilustração 7: Perda de carga versus diâmetro.
A curva obtida, mesmo com a perda de carga zero erroneamente encontrada para o tubo de 1 ½", revela uma relação de potência do tipo y=kxn, onde n<0. Com efeito, segundo a Equação de Darcy, considerando o fator f constante, a perda de carga varia com quinta potência inversa do diâmetro. Senão, vejamos:
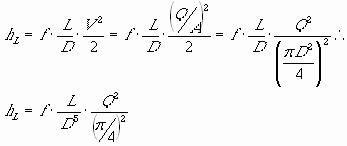
Conforme demonstrado, a perda de carga é proporcional a D-5, para uma vazão Q constante. O gráfico seguinte mostra a relação log-log da perda de carga versus diâmetro (excluindo o tubo de 1 ½", onde a perda de carga foi zero), segundo o experimento.
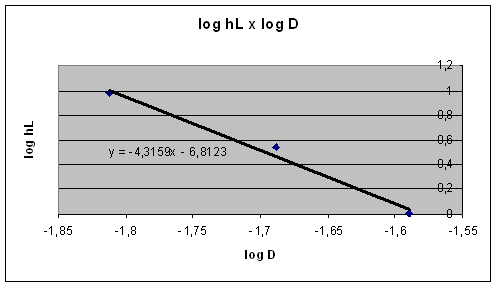
Ilustração 8: Perda de carga versus diâmetro (log-log).
Verifica-se aqui uma reta com inclinação de -4,3159, que seria o expoente do diâmetro nesta relação com a perda de carga. O valor, pois, aproxima-se da proporção teórica, calculada anteriormente, com precisão razoável.
O erro pode ser fruto das medições incorretas obtidas com o tubo de 1 ½", e ainda das dificuldades de medição com o tubo de ½", que pode ter gerado números imprecisos. Além disso, somente sete medidas foram coletadas para este último tubo, e nenhuma na vazão máxima da bomba.
A rugosidade de cada tubo de PVC pode ser calculada tomando-se a perda de carga com a máxima vazão e o número de Reynolds. Aplicando-se a perda de carga na Equação de Moody, sabendo-se V, D e L, obtém-se o fator f. No Diagrama de Moody, com o número de Reynolds, encontra-se a curva ε/D apropriada. Obtém-se assim a rugosidade. Senão vejamos:
Tubo ¾":
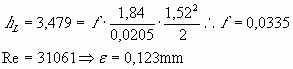
Tubo 1":
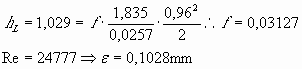
Tubo ½":
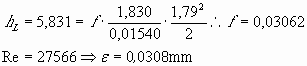
Tubo 1 ½": cálculo não pode ser feito, pois hL foi zero.
Os erros, comparados com o valor tabelado do PVC de 0,0021mm, são:
Rugosidade | Tabelado | Erro |
0,1230 | 0,0021 | 5757,14% |
0,1028 | 0,0021 | 4795,24% |
0,0308 | 0,0021 | 1366,67% |
Tabela 5: Erros das rugosidades calculadas.
Os erros foram bastante elevados, portanto. O experimento não mostrou-se eficiente a ponto de permitir o cálculo da rugosidade dos tubos de maneira precisa.
Apesar de que o cálculo da rugosidade do PVC com os dados obtidos do experimento não se mostrou satisfatório, o experimento foi útil na demonstração da influência da vazão e do diâmetro do tubo sobre a perda de carga.
A visualização da diminuição de pressão a jusante devido a perda de carga, bem como os efeitos sobre ela quando da regulagem da vazão, em tempo real, contribuiu para o entendimento deste fenômeno e para a aplicação das equações de Darcy e uso do Diagrama de Moody.
BELLO, Sergio; LOBO, Paulo. Análise Gráfica de Dados Experimentais. Material didático do Curso de Graduação em Engenharia Elétrica, UNIFACS. Salvador, 1999. Mimeo.
BELLO, Sergio. Perda de Carga em Fluidos Incompressíveis: Roteiro de Prática. Material didático do Curso de Graduação em Engenharia Elétrica, UNIFACS. Salvador, 2001. Mimeo.
FOX, Robert W.; McDONALD, Alan T. Introdução à Mecânica dos Fluidos. 4. edição. Rio de Janeiro, LTC – Livros Técnicos e Científicos Editora S.A., 1995. p. 253 a 285.
MUNSON, Bruce R. et al. Fundamentos da Mecânica dos Fluidos. vol II, versão SI, tradução da 2. edição americana. São Paulo, Editora Edgard Blücher Ltda., 1997. p. 64 a 67.