Refração
Marcos Portnoi
Rafael G. B. Araújo
Romildo Fausto
Victory Fernandes
Engenharia Elétrica - UNIFACS
17.Outubro.1999
http://surf.to/locksmith
"Constituição Brasileira. Artigo Único: todo brasileiro fica obrigado a ter vergonha na cara.."
--
Indíce *
Material Utilizado *Procedimento e Discussão *
Através de atividades realizadas com um recipiente transparente em formato de meia-lua e um papel com marcação de ângulos, verificar o efeito de refração quando a luz passa pela água, causando alteração no ângulo de observação de uma haste, no caso, um pequeno alfinete.
A refração é um fenômeno interessante que acontece com a luz e com qualquer onda eletromagnética. Refratar vem da palavra latina que significa "quebrar". A palavra "fratura" também tem a mesma raiz. De fato, ao se mergulhar um lápis inclinado dentro de um copo cheio de água, o lápis parecerá "quebrado".
O fenômeno da refração ocorre quando a luz ou onda eletromagnética passa de um meio com um determinado coeficiente de refração para outro de coeficiente diferente. O coeficiente de refração, n, é a razão entre a velocidade da luz no vácuo e a velocidade da luz no meio em questão:
O que acontece, de fato, é que a velocidade da luz muda ao passar de um meio, como o ar, para outro, como a água ou vidro. O efeito disso é o desvio do facho de luz sob um determinado ângulo. O coeficiente de refração depende da densidade do meio: aquele é maior, quanto mais denso foi o meio, ou seja, menor a velocidade da luz no meio mais denso.
A frequência da luz não muda quando esta passa de um meio para outro. De acordo com a fórmula:
,
onde v é a velocidade da onda, l (lambda) é a comprimento da onda e f é a frequência, deduz-se que o comprimento de onda tem de mudar. O índice ou coeficiente de refração pode então ser escrito em função dos comprimentos de onda, assim:
,
onde l
0 é o comprimento de onda da luz no vácuo e l é o comprimento de onda da luz no meio.A mudança de velocidade e comprimento de onda na borda de dois materiais causa a mudança de direção da luz. Uma analogia rudimentar para isso seria um carro, inicialmente no asfalto, aproximando-se de uma estrada de lama sob um determinado ângulo agudo. O primeiro pneu a atingir a lama diminuirá de velocidade, enquanto que o pneu do mesmo eixo ainda roda à maior velocidade no asfalto. Isso obrigará o carro a virar, até que ambos pneus estejam na lama e girando à mesma velocidade. Se q 1 é o ângulo do raio relativo à normal do plano de incidência no meio 1, e q 2 é o ângulo relativo à normal no meio 2, então:
onde v1 e l
1 são a velocidade e comprimento de onda no meio 1, etc. Isto é ilustrado na Figura 1.
Figura 1: Lei da Refração.
Esta relação entre os ângulos é chamada de Lei de Snell. A Lei de Snell pode ser deduzida segundo várias maneiras diferentes. Duas deduções famosas são creditadas ao Princípio de Huygens e ao Princípio de Fermat.
O Princípio de Huygens postula que:
Todos os pontos numa frente de onda podem ser considerados como fontes pontuais para a produção de ondas elementares esféricas secundárias. Após um tempo t a nova posição de uma frente de onda é a superfície tangente a estas ondas elementares secundárias.
O Princípio de Fermat, descoberto em 1650, expressa que:
Um raio de luz que se propaga de um ponto fixo para outro ponto fixo segue um trajeto tal que, comparado aos trajetos próximos, o tempo necessário é um mínimo, um máximo ou permanece inalterado (isto é, estacionário).
O desenvolvimento destes princípios, apesar de valiosos e interessantes, fogem ao objetivo deste relatório de experimentos e não será feito.
A Tabela 1 traz alguns índices de refração para vários materiais.
Observe que a tabela especifica os índices para um comprimento de onda único. Isso advém do fato de que geralmente o coeficiente de refração de um material varia com o comprimento de onda da luz. Isso explica o porquê de um facho de luz branca (que é constituída por luz de vários comprimentos de onda diferentes) é decomposta em vários feixes de luz de comprimentos de onda, ao passar por um prisma.
Meio | Índice |
Vácuo (exato) | 1,00000 |
Ar (CNTP) | 1,00029 |
Água (20oC) | 1,33 |
Álcool Etílico | 1,36 |
Vidro Comum | 1,52 |
Poliestireno | 1,55 |
Vidro ou cristal denso | 1,65 |
Safira | 1,77 |
Diamante | 2,42 |
Tabela 1: Índices de refração para comprimento de onda de 589 nm (luz amarela de sódio).
O efeito conhecido como arco-íris resulta da luz solar passando por gotículas de água em suspensão na atmosfera, gotículas essas que funcionam como um prisma. O arco-íris e geralmente visto no céu oposto ao sol, logo após ou logo antes da chuva, e também junto a sprays de cachoeiras. Um arco-íris é composto de dois arcos: o mais brilhante, chamado de primário, tem as cores arranjadas com o vermelho para fora da circunferência; o segundo arco, chamado de arco-íris secundário, é menos brilhante e apresenta as cores em ordem inversa.
Quando a luz do sol entra numa gotícula de água em suspensão, ela é refratada e então refletida na "parede" oposta da gotícula. Como a luz do sol é branca, ou seja, composta de luz de praticamente todos os espectros visíveis de comprimento de onda, cada comprimento de onda é refratado sob um ângulo ligeiramente diferente dos demais, o que o "separa" dos outros, causando o agradável efeito de degradê do arco-íris.
O arco secundário é formado quando o facho de luz é refletido duas vezes no interior da gotícula de água, causando a reversão e a perda de brilho. O grande número de gotículas funciona como um prisma gigante, redondo, finalizando o efeito. Ver Figura 2.
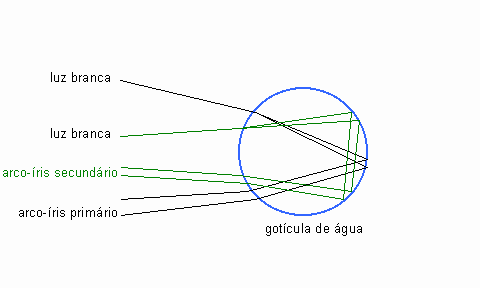
Figura 2: Refração de luz solar dentro de uma gotícula de água.
Na Figura 2, dois fachos de luz solar são indicados. Um deles, incidindo na gotícula sob um determinado ângulo, é refratado ao passar pela borda da gotícula, refletido no extremo oposto desta, refratado mais uma vez ao sair da gotícula e então ganha de novo o ar. Este feixe forma o arco-íris primário.
Um segundo feixe, novamente incidindo sobre a gotícula segundo um determinado ângulo, é refratado ao passar para o meio aquoso do interior da gotícula e sofre uma reflexão. O ângulo que o feixe entrou na gotícula permite que haja mais uma reflexão dentro da gotícula. Esta segunda reflexão inverte o facho, e este então sai da gotícula com brilho menor, devido a perdas de intensidade dentro da gotícula. Este é o arco-íris secundário, formado próximo ao primário.
As cores do arco-íris só podem ser vistas, na prática, se o ângulo de reflexão entre o sol, a gotícula e a linha de visão do observador estiver entre 40o e 42o. Fora desta faixa, o efeito arco-íris não é visível.
Um recipiente em formato de meia-lua, de plástico transparente, cujo interior pode ser preenchido com líquido.Papel rosa-dos-ventos com ângulos de 0o a 360o marcados.Alfinetes.Régua.
Ver Figura 3 para uma representação do recipiente em formato de meia-lua, visto de cima. Este recipiente tem um lado com formato de semicircunferência e um outro lado reto. Neste lado reto, foi feita uma marcação em seu ponto médio. O recipiente é então colocado por sobre o papel de ângulos, de forma que o lado reto esteja alinhado com o eixo x do papel, e a marcação do ponto médio, com a origem dos ângulos.
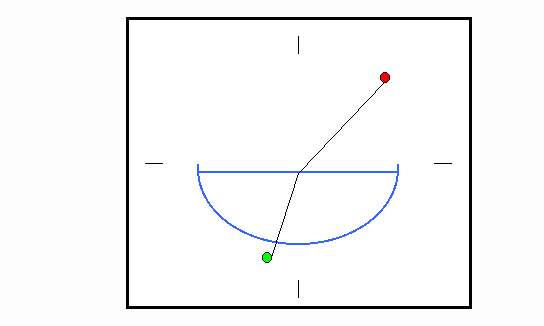
Figura
3: Recipiente em meia-lua, vista superior.O procedimento consiste em se colocar um alfinete, fincado de modo vertical, num ângulo qualquer na parte voltada para o lado reto da meia-lua. Este alfinete está indicado em vermelho na Figura 3. Então, sua imagem é observada através do lado curvo da meia-lua, de modo que sua imagem fique alinhada com a marcação também vertical no lado reto da meia-lua. A imagem do alfinete será refratada pelo líquido dentro do recipiente meia-lua, por conseguinte, será desviada e o ângulo de desvio pode então ser medido, conforme demonstrado na Figura 3. Um outro alfinete é posicionado pelo lado curvo de modo a marcar a imagem refratada do alfinete original. Este outro alfinete é indicado em verde.
Fez-se então 4 medidas, segundo vários ângulos. Para cada ângulo escolhido, posicionou-se um alfinete pelo lado reto da meia-lua, observou-se este alfinete pelo lado curvo, alinhou-se sua imagem com a marcação do ponto médio do lado reto (visível pela água) e marcou-se esse alinhamento com outro alfinete, o mais perto possível da parede da meia-lua. Os alfinetes sempre foram removidos, depois de feitas as marcações, de modo a não poluir o campo de visão. Os ângulos então puderam ser medidos, ao final, traçando-se uma reta de apoio do furo dos alfinetes ao centro do papel de ângulos. Na borda deste papel, estão graduados os ângulos, podendo então ser facilmente medidos. A Tabela 2 abaixo mostra os dados coletados. A primeira coluna indica o ângulo refratado, ou seja, o ângulo pelo qual o alfinete foi observado pelo lado curvo. A segunda coluna indica o ângulo de incidência, ou seja, o ângulo medido entre o alfinete pelo lado reto à normal da superfície reta. As colunas seguintes contêm os senos dos respectivos ângulos, e a última coluna, a razão entre os senos do ângulo de incidência e o ângulo refratado.
q r | q i | senq r | senq i | senq i/ senq r | |
1 | 14,5o | 20o | 0,2504 | 0,3420 | 1,366 |
2 | 29,5o | 40o | 0,4924 | 0,6428 | 1,305 |
3 | 41,5o | 60o | 0,6626 | 0,8660 | 1,307 |
4 | 35o | 50o | 0,5736 | 0,7660 | 1,335 |
Tabela 2: Dados coletados no experimento.
Aqui a relação da Lei de Snell é utilizada. Considerando o índice de refração do ar aproximadamente igual a 1, vem:
Usando o método dos mínimos quadrados, foi possível encontrar o melhor coeficiente angular para a reta representada por senq i(y) e senq r(x). Este valor representa o índice de refração experimental da água nágua, que foi de 1,282.
Pode-se agora avaliar o erro experimental deste procedimento, tomando-se o valor tabelado para o índice de refração da água de 1,33. Assim,
Neste experimento, os erros usualmente são menores que 1%. O valor aqui encontrado de 3,61%, apesar de alto se comparado ao histórico, não invalida o experimento. Posteriormente à tomada de medidas, observou-se que o marco no centro ou ponto médio do lado reto do recipiente em meia-lua era falho, pois continha um desvio acentuado numa das pontas. Isso sem dúvida dificultava o alinhamento do ponto médio com a origem dos ângulos, sendo uma fonte considerável de erro.
Por outro lado, não se pode garantir que a água utilizada no experimento condiz com o índice tabelado de 1,33, tampouco que a superfície transparente do recipiente em meia-lua não contribui para o desvio das imagens. O erro encontrado de 3,61% é portanto extremamente razoável para as condições dos procedimentos.
Os experimentos realizados possibilitaram calcular o índice de refração da água com precisão razoável, usando de equipamento simples e facilmente compreensível. O cálculo também permitiu demonstrar a validade da relação contida da Lei de Snell, onde o produto do seno do ângulo de incidência e o coeficiente de refração do meio é igual ao produto do seno do ângulo refratado e o índice de refração do outro meio.
É sempre uma honra poder repetir observações realizadas séculos atrás por gigantes como Christiaan Huygens e Pierre Fermat, nomes que enobrecem a Ciência.
Halliday, David et al. (1992) Física 4; vol. 4, 4. Edição; LTC Livros Técnicos e Científicos S.A., Rio De Janeiro, RJ; p. 14 a 26.
Microsoft Encarta 97 Encyclopedia, (1996)
Copyright 1993-1996, Microsoft Corporation (
Burley, Ian et al. Theoretical Physics at the University of Winnipeg [online].