[CE 160 homepage]
CE 160
First Exam
First Semester, 2002-2003
exam date: July 18, 2002
coverage: deterministic and nondeterministic finite automata,
regular expressions (approximately chapters 2 and 3 of [IALC2] ) [ answers]
- How many distinct DFA's are there with input
alphabet {0,1} with exactly two reachable states
A and B, with A as the start state, and with
exactly one accepting state?
- Draw transitions diagrams for any eight of the
DFA's described in part (a).
[answer]
- Simplify as much as possible: 1+0(00)*(1+01).
Note: The regular expression occurs as the regular
expression 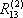 in
doing exercise 3.2.2, p. 106 of [IALC2].
in
doing exercise 3.2.2, p. 106 of [IALC2].
[answer]
- Design a DFA whose language is the set of all strings
over {0,1,2,3,4,5,6,7,8,9} that evaluate to nonzero
integers divisible by 3 when interpreted as decimal
numbers. State the divisibility rule you are using.
Note: This question was suggested by Mark Bendicion.
[answer]
Convert the following e-NFA to an
equivalent DFA in the form of a transition diagram:
| |
e
|
a
|
b
|
c
|
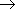 p p
|
|
{p,q}
|
{p,r}
|
{p}
|
q
|
{r}
|
{r}
|
{r}
|
{r}
|
r
|
{s}
|
{s}
|
{s}
|
{s}
|
*s
|
|
|
|
|
[answer]
- Write a regular expression representing the set of all
strings over {0,1}with an equal number of 0's and 1's,
such that no prefix has two more 0's than 1's, nor two
more 1's than 0's. Simplify as much as possible. Hint:
It may help to instead design a DFA and obtain a regular
expression by eliminating states.
Note: This question is Exercise 3.1.3, p. 90 of [IALC2].
[answer]
Some answers:
- The are 24 such DFA's:
A is reachable since it is the start state. For B to be
reachable, the DFA must transition to B on at least one
of the input symbols. Hence there are only three possible
ways of defining transitions from A:
| |
0 |
1 |
 A A |
B |
B |
| |
0 |
1 |
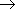 A A |
A |
B |
| |
0 |
1 |
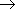 A A |
B |
A |
For each way of defining transitions from A, there are
four ways of defining the transitions from B. And for each
way of defining transitions for the DFA, there are two
choices for the accepting state. This amounts to 3*4*2=24
distinct DFA's.
- 1+0(00)*(1+01)
= 1 + 0(00)*1 + 0(00)*01
= 1 + 01 + 0(00)1 + 0(00)(00)1 + ... + 0(00)*01
= 1 + 01 + 0(00)1 + 0(00)(00)1 + ... + 001 + 0(00)01 +
0(00)(00)01 +...
= 0*1
- A number is divisible by 3 if the sum of its digits is
divisible by 3. Hence we only have to keep track of the
remainder of a running sum of the digits when this sum is
divided by 3. Since addition is commutative and a given
digit contributes exactly the same amount to the
remainder regardless of place value, we don't even have
to worry about which is the most significant digit.
We need three states corresponding to the 3 possible
remainders, and one more state where the DFA stays as
long as the input digits consist only of zeros. A
transition table for the DFA is
| |
0 |
3,6,9 |
1,4,7 |
2,5,8 |
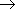 A A |
A |
[0] |
[1] |
[2] |
| *[0] |
[0] |
[0] |
[1] |
[2] |
| [1] |
[1] |
[1] |
[2] |
[0] |
| [2] |
[2] |
[2] |
[0] |
[1] |
.
- A transition table for the equivalent DFA is
| |
a |
b |
c |
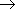 p p |
pqrs |
prs |
p |
| *pqrs |
pqrs |
prs |
prs |
| *prs |
pqrs |
prs |
ps |
| *ps |
pqrs |
prs |
p |
.
Draw the transition diagram.
- Note that the start state should be an accepting state
since e is in the language. Without the condition that no
prefix "have two more 0's than 1's, nor two more 1's
than 0's" it would be impossible to design the DFA
(Prove this using the pumping lemma).
With the added condition, we only need to monitor the
quantity
n = # of 0's seen so far - # of 1's seen so
far.
Based on the condition, if ever n becomes 2
or -2, the DFA should go into a dead state and stay there,
since the current string violates the condition and the
current string would be a prefix of whatever the full string
turns out to be. We don't really need to keep track of n once
we're in the dead state. The only other states we need are
those corresponding n = 0, n = 1, and n = -1. The state for n
= 0 is the lone accepting state and also the start state. A
transition table for the DFA is
| |
0 |
1 |
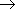 *[0] *[0] |
[1] |
[-1] |
| [1] |
d |
[0] |
| [-1] |
[0] |
d |
| d |
d |
d |
Draw the transition diagram.
In obtaining the regular expression, the dead state is very
easily eliminated. Once this is done, the two nonaccepting
states are eliminated and converted to loops.
Final answer: (01+10)*.
This page has been accessed

times since July 20, 2002.