[Lui's homepage] [DSP homepage]
Lab Exercise:
Magnitude Response
This exercise should be done using Excel.
In this exercise you are to use Excel to obtain the graph of the magnitude response of a finite impulse response (FIR) filter. The FIR filter is specified by the difference equation,
M-1
y(n) = sum h(k)x(n-k)
k=0
where M = 64, and the coefficiets h(n), n = 0,...,63, are as follows:
h(0) = h(63) = -0.000158126130000595
h(1) = h(62) = -0.000478357664687351
h(2) = h(61) = -0.000801661859271876
h(3) = h(60) = -0.00110308549297515
h(4) = h(59) = -0.00132172249376453
h(5) = h(58) = -0.00136202669388539
h(6) = h(57) = -0.0011120329442612
h(7) = h(56) = -0.000476799980284982
h(8) = h(55) = 0.000579729798449221
h(9) = h(54) = 0.00199526015169846
h(10) = h(53) = 0.00358456090475661
h(11) = h(52) = 0.00504093135426444
h(12) = h(51) = 0.00597041268497614
h(13) = h(50) = 0.00595859162735932
h(14) = h(49) = 0.0046618924422662
h(15) = h(48) = 0.00190795478936417
h(16) = h(47) = -0.00221519988670355
h(17) = h(46) = -0.007302606005794
h(18) = h(45) = -0.0126263939533596
h(19) = h(44) = -0.0171907724840236
h(20) = h(43) = -0.0198475323191142
h(21) = h(42) = -0.0194597067397005
h(22) = h(41) = -0.0150902257239541
h(23) = h(40) = -0.00618501702109644
h(24) = h(39) = 0.00728221471782563
h(25) = h(38) = 0.024732532464351
h(26) = h(37) = 0.0449911864134062
h(27) = h(36) = 0.0663897640447006
h(28) = h(35) = 0.0869513189490387
h(29) = h(34) = 0.104634017163135
h(30) = h(33) = 0.117597777544398
h(31) = h(32) = 0.124453122342888 .
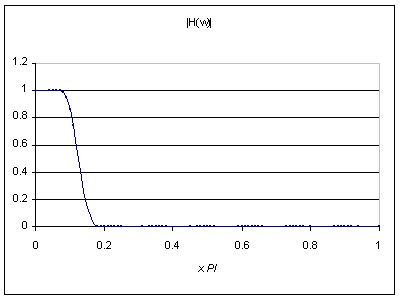
Use Excel to determine the magnitude response of this system, and graph the magnitude response against frequency. Show all intermediate computations. Be able to answer all questions related to this exercise.
Answer: