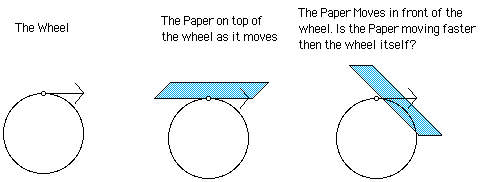
X-Ploration of the turning of a wheel
By Crean
The Question
There is a wheel and a piece of paper is placed on top of the wheel. As the wheel rotates the piece of paper seems to fall off the top of the wheel in the direction of rotation. The piece of paper appears to be moving faster than the wheel itself. What is going on here?

The Experiment
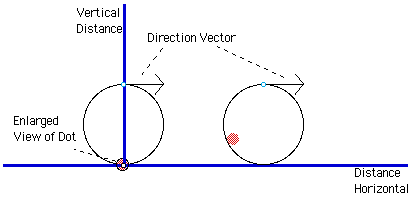
The experiment is to give us some insight into the behavior of the wheel and possibly answer the question, posed. The experiment was conducted as follows:
Lay out a lengthwise measuring tape and place a wheel with a red dot marked on the perimeter. Prior to this we divided the wheel by making marks at every 45o rotational point as follows:
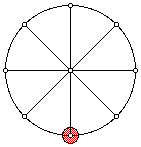
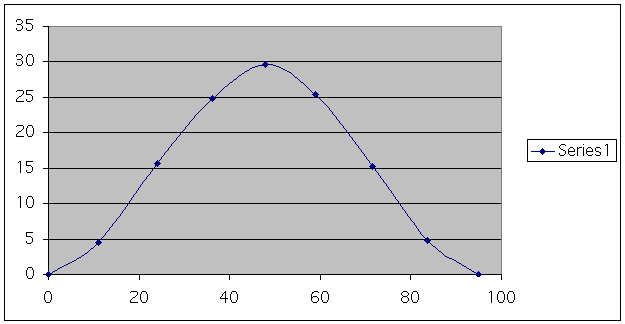
Now we rolled the wheel along the measuring tape recording the height of the red dot and the distance that the wheel has traveled. The following table of data is the results of the experiment:
|
H-Dist |
Height of Dot |
|
0 |
0 |
|
11.1 |
4.5 |
|
24.1 |
15.6 |
|
36.1 |
24.9 |
|
47.8 |
29.7 |
|
59 |
25.4 |
|
71.6 |
15.3 |
|
83.7 |
4.8 |
|
95 |
0 |
|
All in millimeters |
|
The below graph corresponds to horizontal distance traveled by the wheel to the height of the dot based upon the distance
(all in millimeters).
Now there was a great deal of x-perimental error in performance of this experiment because of measurement flaws etc. Note that since we took 45o angle measure we arrive at 8 measurements (360 o / 45 = 8) where the first and the last measurements in the table of values are one complete rotation. If we were to perform this experiment with finer and finer angle intervals then we would arrive at a fine graph covered below (the intervals are different, but the graph looks like it should).
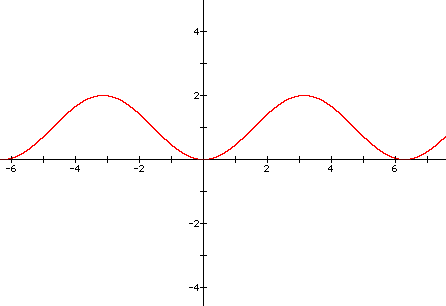
This graph corresponds Angle measure with the height of the point measured (horizontal/vertical axis respectively).
Now let us examine the specifics of the location of the point on the wheel.
Notes: The above equation is one component of the below:
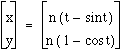
In a parametric form
So now we have a way to locate the position of the red dot on the wheel at any time or location along some horizontal axis. The following graph corresponds to the height versus distance as well as the rate of change of the wheel (the red dot):
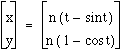
The red circle corresponds to one cycle of the point based upon the parameterization:
For the dot height

From this picture we can see that the rate of change gets less and less till at the top of the circle the tangent vector is equal to zero (the x intercept of the green graph) and then the rate starts to decline. Now let us think about this non-mathematically. If the wheel is moving at whatever rate it is moving at, fine and dandy. If there is a piece of paper placed on top of the wheel then this paper (think of it as being stiff) will be tangent to the circle. Now as we turn the wheel, the rate of change of the paper will slowly decline till it is matched to the rate of the wheel at the top (the derivative equals zero) and then starts to decline. But how fast will the paper be moving. Well the paper is "at rest" initially and we then place it on top of the wheel. The paper will be moving at the rate of the wheel along with its rate of change. So if the paper was stuck to the wheel (er.. not subject to the forces of gravity) then the papers speed will modulate back and forth as in the graph of the position of the dot, only being equal to the speed of the wheel when it is at the top of the graph (or the bottom - both times have a rate of change of zero) so at all other times, the paper will be moving faster to the wheel, because it will be moving at the rate that the wheel is moving plus the rate of change of it's rotational vector. Let us look at the following picture, which should clear some of this up:


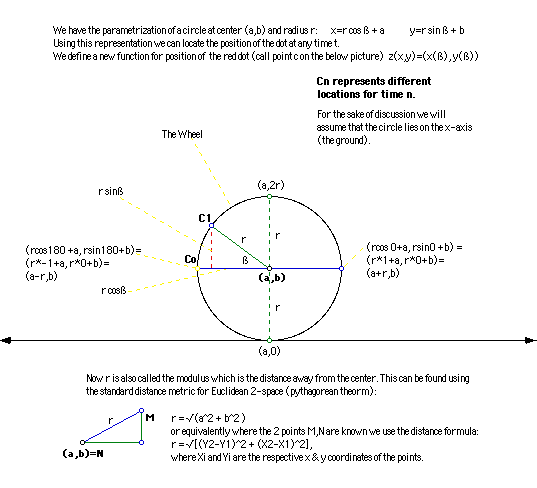
Vector representation

Now we can model this using a physics/mathematical model.
Notes:
p radians=180oWith a rigid object and a point rotating around the rigid object, as the particle in question moves along the circle it sweeps out an arc.

We define the angular speed w* as the ratio of angular displacement to the time: w* = (ß
2-ß1)/(t2-t1)=Æß/Æt. Now the instantaneous angular speedw = lim
Æt ->0 Æß/Æt. If w changes with some temporal displacement then the rate of change is changing --> acceleration å* = (w2-w1)/(t2-t1)=Æw/Æt, with the instantaneous acceleration å = lim Æt ->0 Æw/Æt.Note that when rotating around a fixed axis, every particle on a rigid object has the same angular speed and angular acceleration. Now the tangential speed of a point on a rotating object equals the distance of that point from the axis of rotation multiplied by the angular speed! Although every point on the rigid object has the same angular speed not every point has the same linear speed. This was shown in the vector representation above. Some more 'advanced' mathematics involving the tangent vectors follows:
The parametric equations for a circle of radius r: x= r cos t and y= r sin t.
For a body moving uniformly around the circle: x' = -r sin t & y' = r cost.
and x" = -r cos t, and y" = -a sin t.
When normalized (set about the origin), the former equation for the unit tangent vector (-sin t, cos t). The circle can also be parameterized by the rational functions:
x = (1-t2)/t (1+t)
y =2t/(1+t2)
Let
* (a,b) stand for the definite integral from a to b. * is the indefinite integral.The arc length s (t) =
* ds =* ÷ (x'2 +y'2) dt = rt.Curvature is k (t) = (x'y" - y'x")/(x'2+y'2)3/2 = 1/r
Tangential angle o (t) =
* k (t) dt = t/aSo simply put the paper is moving faster than the wheel because it is being pushed in the direction of the wheel (er... greater linear speed) and can be treated almost like a tangent vector. The wheel itself is moving at a given speed (velocity vector actually) and the paper is moving at this rate in addition to the tangent rate of change along the circles edge. So the paper will move "faster" than the wheel. Believe me? Good, either way. The following are some graphs of distance of the dot versus height, the height of the dot versus the angle traversed up to a given angle, and the distance versus the angle:
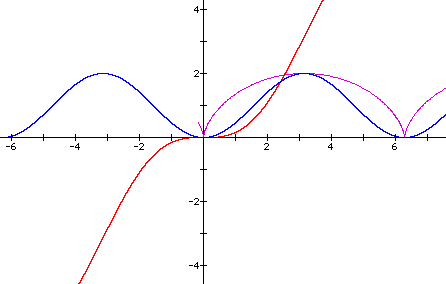
The Period can be declared as it need be.

![]()
![]()
Purple, Red, Blue graphs respectively.
Other cases may be investigated as one deems of import with some interesting observations regarding the radius (hint).
The spread sheet data follows:
|
Degree Count |
Radian Count |
Sine |
Cosine |
Distance Ant |
Height Ant |
|
0 |
0 |
0 |
1 |
0 |
0 |
|
10 |
0.17453293 |
0.17364818 |
0.98480775 |
0.00088475 |
0.01519225 |
|
20 |
0.34906585 |
0.34202014 |
0.93969262 |
0.00704571 |
0.06030738 |
|
30 |
0.52359878 |
0.5 |
0.8660254 |
0.02359878 |
0.1339746 |
|
40 |
0.6981317 |
0.64278761 |
0.76604444 |
0.05534409 |
0.23395556 |
|
50 |
0.87266463 |
0.76604444 |
0.64278761 |
0.10662018 |
0.35721239 |
|
60 |
1.04719755 |
0.8660254 |
0.5 |
0.18117215 |
0.5 |
|
70 |
1.22173048 |
0.93969262 |
0.34202014 |
0.28203786 |
0.65797986 |
|
80 |
1.3962634 |
0.98480775 |
0.17364818 |
0.41145565 |
0.82635182 |
|
90 |
1.57079633 |
1 |
6.123E-17 |
0.57079633 |
1 |
|
100 |
1.74532925 |
0.98480775 |
-0.1736482 |
0.7605215 |
1.17364818 |
|
110 |
1.91986218 |
0.93969262 |
-0.3420201 |
0.98016956 |
1.34202014 |
|
120 |
2.0943951 |
0.8660254 |
-0.5 |
1.2283697 |
1.5 |
|
130 |
2.26892803 |
0.76604444 |
-0.6427876 |
1.50288358 |
1.64278761 |
|
140 |
2.44346095 |
0.64278761 |
-0.7660444 |
1.80067334 |
1.76604444 |
|
150 |
2.61799388 |
0.5 |
-0.8660254 |
2.11799388 |
1.8660254 |
|
160 |
2.7925268 |
0.34202014 |
-0.9396926 |
2.45050666 |
1.93969262 |
|
170 |
2.96705973 |
0.17364818 |
-0.9848078 |
2.79341155 |
1.98480775 |
|
180 |
3.14159265 |
1.2246E-16 |
-1 |
3.14159265 |
2 |
|
190 |
3.31612558 |
-0.1736482 |
-0.9848078 |
3.48977376 |
1.98480775 |
|
200 |
3.4906585 |
-0.3420201 |
-0.9396926 |
3.83267865 |
1.93969262 |
|
210 |
3.66519143 |
-0.5 |
-0.8660254 |
4.16519143 |
1.8660254 |
|
220 |
3.83972435 |
-0.6427876 |
-0.7660444 |
4.48251196 |
1.76604444 |
|
230 |
4.01425728 |
-0.7660444 |
-0.6427876 |
4.78030172 |
1.64278761 |
|
240 |
4.1887902 |
-0.8660254 |
-0.5 |
5.05481561 |
1.5 |
|
250 |
4.36332313 |
-0.9396926 |
-0.3420201 |
5.30301575 |
1.34202014 |
|
260 |
4.53785606 |
-0.9848078 |
-0.1736482 |
5.52266381 |
1.17364818 |
|
270 |
4.71238898 |
-1 |
-1.837E-16 |
5.71238898 |
1 |
|
280 |
4.88692191 |
-0.9848078 |
0.17364818 |
5.87172966 |
0.82635182 |
|
290 |
5.06145483 |
-0.9396926 |
0.34202014 |
6.00114745 |
0.65797986 |
|
300 |
5.23598776 |
-0.8660254 |
0.5 |
6.10201316 |
0.5 |
|
310 |
5.41052068 |
-0.7660444 |
0.64278761 |
6.17656512 |
0.35721239 |
|
320 |
5.58505361 |
-0.6427876 |
0.76604444 |
6.22784122 |
0.23395556 |
|
330 |
5.75958653 |
-0.5 |
0.8660254 |
6.25958653 |
0.1339746 |
|
340 |
5.93411946 |
-0.3420201 |
0.93969262 |
6.2761396 |
0.06030738 |
|
350 |
6.10865238 |
-0.1736482 |
0.98480775 |
6.28230056 |
0.01519225 |
|
360 |
6.28318531 |
-2.449E-16 |
1 |
6.28318531 |
0 |
|
Note that 180 degrees corresponds to pi and 360 degrees is 2 pi |
|||||
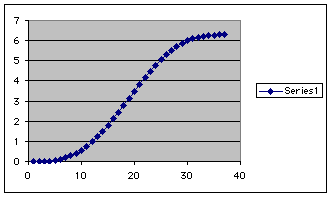
This graph corresponds to distance versus angle measure
Vertical/Horizontal Axis respectively.

This Corresponds to the height versus angle measure as first measured.
Vertical/Horizontal Axis respectively.
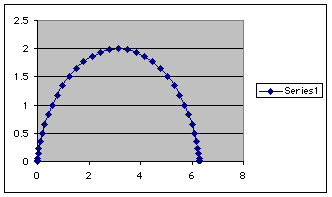
This Last Graph corresponds to the distance versus height.
Horizontal/Vertical respectively.
"...namely that there is what in both German and English is called "Zeitgeist", a form unique time-cum-thought quality, leading to surprisingly similar albeit completely independent models of thought, technical inventions, political truths and so on." - Fra.:U.D.
End