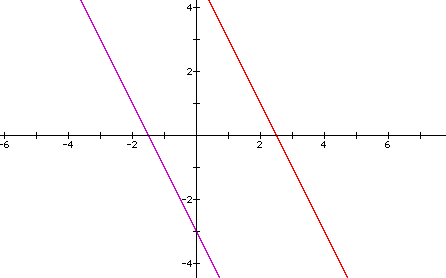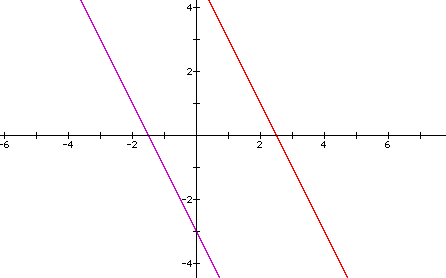Translations
by Frater Elijah
By a translation, we mean a rigid motion whose equations are:
x' = x + a and y' = y + b for real numbers a & b.
Given the translation x' = x + 3 and y' = y + 2.
Find the equation of the images of the graphs of each of the
following cases.
We have 2x + y - 5 = 0. Re arranging gives y = -2x +5, a linear
equation.
Now composition gives (y +2) = -2(x+3) + 5 --> y = -2x -6
+5 -2 = -2x-3
Comparing we have y=-2x+5 and y=-2x-3 so this is a line shifted
to the left.
Looking at x2 +y2 = 1 (the unit circle), under
x' and y' we have (x+3)2 + (y+2)2 = 1
- x2 + 6x + 9 + y2 + 4y + 4 = 1 --> x2
+ 6x + y2 + 4y = -12 comparing these graphs shows.
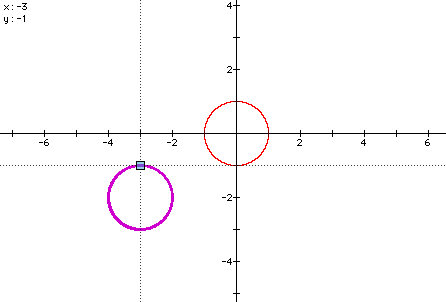 A shift in the unit circle, cool!
Now for y = x2. We have (y + 2) = (x + 3)2
--> y = x2 +6x +7.
A shift in the unit circle, cool!
Now for y = x2. We have (y + 2) = (x + 3)2
--> y = x2 +6x +7.
 Cool a parabolic shift!
Cool a parabolic shift!
Return