Bill Majoros
william.majoros@celera.com
December 9, 2000
Abstract
Two of these algorithms, backpropagation neural networks and genetic programming, employ an element of randomness which renders them nondeterministic, so that each algorithm singly can produce different results on identical runs. For this reason, it is advisable to run each algorithm multiple times on each problem, to give the algorithm an opportunity to search a larger portion of its model space. Unfortunately, each run of these algorithms can take a considerable amount of time, depending on the parameterization of the model and the size of the problem to be solved.
In the study mentioned above, the neural networks and genetic programs were trained under fairly stringent resource constraints, and it was suggested that the results might have been different had the available computational resources been significantly increased.
The purpose of the present study was to investigate this possibility by re-running the neural networks and genetic programs on the same problem set, but using a significantly faster computer and a longer time limit. The combination of faster clock speed and longer time limit produced a hundred-fold increase in computational power. It was hoped that such an increase would be sufficient to reveal any effect that resource constraints may have had on the ability of these two algorithms to perform competitively in the previous study.
As an additional minor enhancement to the previous study, another classification technique, linear discriminant analysis, was added to the set of algorithms to be compared, bringing the total to eight algorithms, or thirteen algorithm variants.
Algorithms
All of the algorithms employed in [Majoros 2000] will
be compared here, with only the genetic programming and backpropagation
neural nets being exercised anew. Abbreviations used in the previous
study will be utilized again here: RND=random guessing, MAJ=majority rule,
BAY=naive Bayes classifier, NET=neural network, TRE=decision tree, NC=nearest
centroid with Euclidean distance, KN=k-nearest-neighbors, FS=k-nearest-neighbors
with feature selection, MAH=k-nearest-neighbors using Mahalanobis distance,
KNW=k-nearest-neighbors with weighted attributes, KWM=k-nearest-neighbors
using Mahalanobis distance with weighted attributes, NCM=nearest-centroid
using Mahalanobis distance, REG=linear regression, and GP=genetic programming.
An additional algorithm, linear discriminant analysis, also known as discriminant function analysis (DFA), is employed. Discriminant analysis is a well-known statistical technique developed by R. A. Fisher in 1936 and provided by many commercial statistical packages [Many 1994]. This method uses eigenvalues and eigenvectors to identify a set of linear functions which optimally separate classes. All of the linear functions are evaluated for each test case and the resulting values are subjected to the nearest centroid algorithm (NCM) to produce a classification. C++ code for computing the linear functions was adapted from [Masters 1995].
Computing Resources
All programs were executed on an 8-node cluster consisting
of 800 MHz Pentium III processors grouped into dual processor machines,
each having 128 Mb of RAM. All four machines ran Red Hat Linux version
6.2 compiled for symmetric multiprocessing. "Fast ethernet" connections
provided a 100Mbps communication channel.
For GP and NET, eight processes were executed simultaneously, one per processor, with randomized initial conditions. Completed processes were followed by new invocations, until at least eight hours of wall-clock time had elapsed (per algorithm, per problem). Only the highest score was kept for each problem.
This repetitive approach to utilizing greater computational resources allows searching through both the parameter space of the algorithm, as well as the model space constrained by a given parameterization. Because each of the many models (often thousands) induced during this search was evaluated in the context of the test set, one can expect there to be a slight chance of overtraining on the test set. However, because training was performed using the training set, inadvertent exploration of the test set was limited to the random search that occurred as a result of random model initialization at the beginning of each run (i.e., initial synapse weights in NET, and the initial population in GP). Thus, the slight chance of overtraining with respect to the test set should not be expected to noticeably affect the results of this study.
Statistical Analyses
All statistical analyses are as described in [Majoros
2000], with the exception of the t-test described below. Briefly,
analysis of variance (ANOVA) was applied to both scores and ranks, for
both real-world problems and the entire problem set (i.e., four analyses
in all), followed by pairwise comparisons using the Tukey test.
Differences in scores between this and the previous study for GP, and separately for NET, were subjected to a paired t-test.
Significance levels were set a 0.05. All analyses were performed using unpublished software written by the author. Statistical procedures and critical values were taken from [Zar 1996].
problem
NET GP DFA
problem NET GP DFA
ocr
59% 10% 66% hepatitis 86%
99% 76%
income
85% 82% 79% brst-cancer 99% 98%
96%
pendigits 94%
33% 82% ecoli 83%
68% 81%
optdigits 96%
28% 89% iris
99% 100% 84%
bands
82% 80% 67% yeast
49% 38% 47%
ind-diabetes 75% 77% 76%
abalone 27% 28% 22%
dermatology 99% 69%
96% mpg 88%
79% 78%
mushroom 100% 99% 64%
scale 97% 100% 73%
haberman 69%
77% 62% cmc
57% 52% 47%
liver
64% 70% 64% echocardio 83%
86% 68%
tae
68% 64% 63% monk1
86% 100% 52%
glass
65% 62% 58% monk2
71% 67% 51%
wine
100% 91% 98% monk3
97% 97% 76%
water-treatmt 75% 60% 68%
nl1 100% 97%
98%
vote
97% 99% 95% nl2
94% 90% 89%
soybean 91%
38% 89% nl3
89% 80% 79%
crx
89% 84% 84% nl4
96% 93% 91%
hypo
94% 94% 0% nl5
83% 91% 81%
ionosphere 98% 99%
62% nl6 96%
92% 92%
Table 1: New accuracy scores. Improvements are underlined.
Improvements were made by NET on 27/38=71% of the problems, and by GP on 32/38=84% of the problems. However, these differences were statistically significant for neither NET (t=0.82<t0.05(1),37=1.687, P>0.1) nor GP (t=0.66<t0.05(1),37=1.687, P>0.25).
The original scores given in [Majoros 2000] are reproduced
in Table 2. The occurrence of ni in the table indicates that
the algorithm in question encountered a noninvertible matrix, and had to
be aborted.
problem
RND MAJ BAY NET TRE NC KN FS MAH KNW KWM NCM REG GP
ocr
4% 4% 75% 59% 86% 58% 84% 89% 85% 56% 47% 66% 82% 8%
income
50% 76% 77% 85% 83% 55% 71% 73% 78% 70% 74% 79% 82% 80%
pendigits 10% 10% 79% 54%
94% 78% 97% 97% 96% 96% 96% 82% 95% 23%
optdigits 10% 10% 73% 69%
86% 89% 97% 98% ni 96% ni ni ni 24%
bands
50% 51% 51% 74% 69% 67% 72% 72% ni 79% ni ni 51% 74%
ind-diabetes 50% 64% 61% 68% 73% 65% 74% 76%
75% 69% 63% 76% 78% 76%
dermatology 17% 31% 53% 98% 97% 45% 87%
98% 84% 52% 74% 96% ni 63%
mushroom 50% 52% 100%100%99%
64% 100%100% ni 100% ni ni 79% 99%
haberman 50% 68% 69%
68% 73% 75% 71% 72% 71% 65% 65% 62% 68% 76%
liver
50% 49% 50% 64% 61% 67% 58% 60% 54% 63% 55% 64% 64% 67%
tae
33% 27% 55% 61% 60% 43% 53% 53% 59% 55% 57% 63% 52% 40%
glass
14% 31% 49% 43% 64% 40% 69% 69% 64% 62% 54% 58% ni 60%
wine
33% 36% 39% 98% 93% 71% 69% 71% 97% 67% 81% 98% 99% 88%
water-treatmt 8% 48% 48% 62% 66% 18% 55% 63%
56% 53% 57% 68% ni 48%
vote
50% 61% 79% 97% 97% 88% 89% 96% 93% 89% 80% 95% 96% 99%
soybean
5% 13% 82% 91% 85% 51% 60% 84% 88% 60% 72% 89% ni 16%
crx
50% 55% 65% 86% 82% 67% 66% 73% 83% 65% 65% 84% 84% 84%
hypo
20% 92% 95% 94% 97% 0% 96% 96% ni 94% ni ni ni
93%
ionosphere 50% 82% 95% 96% 97%
62% 95% 94% ni 91% ni ni ni 97%
problem
RND MAJ BAY NET TRE NC KN FS MAH KNW KWM NCM REG GP
hepatitis 50% 81% 80% 81%
83% 68% 74% 78% 83% 76% 80% 76% 76% 85%
brst-cancer 50% 66% 95% 97% 94% 96% 97%
97% 93% 97% 93% 96% 96% 97%
ecoli
13% 39% 40% 72% 80% 81% 86% 86% ni 85% ni ni ni
59%
iris
33% 31% 97% 93% 97% 97% 100%100%89% 96% 81% 84% 96% 99%
yeast
10% 27% 27% 49% 52% 48% 59% 59% 56% 54% 52% 47% ni 34%
abalone
3% 17% 21% 23% 23% 6% 26% 24% 22% 25% 19% 22% ni 17%
mpg
33% 45% 50% 85% 80% 70% 77% 78% 81% 76% 81% 78% 82% 77%
scale
33% 46% 90% 93% 79% 72% 92% 92% 91% 92% 90% 73% 89% 100
cmc
33% 40% 48% 56% 51% 39% 53% 53% 48% 51% 47% 47% 50% 42%
echocardio 50% 82% 79% 82% 82%
56% 76% 77% 79% 79% 80% 68% 82% 85%
monk1
50% 50% 71% 86% 93% 50% 70% 75% 73% 70% 62% 52% 52% 83%
monk2
50% 67% 62% 71% 87% 67% 79% 78% 68% 80% 72% 51% 67% 67%
monk3
50% 47% 97% 81% 97% 64% 67% 89% 84% 67% 63% 76% 77% 97%
nl1
50% 51% 85% 99% 87% 93% 96% 96% 95% 96% 95% 98% 98% 96%
nl2
50% 59% 89% 90% 91% 88% 92% 92% 91% 81% 82% 88% 89% 89%
nl3
50% 60% 76% 85% 79% 79% 89% 89% 86% 71% 70% 79% 79% 76%
nl4
50% 52% 82% 89% 85% 89% 90% 92% 89% 69% 69% 91% 90% 90%
nl5
50% 52% 83% 83% 82% 81% 82% 83% 81% 56% 54% 81% 82% 83%
nl6
50% 50% 88% 85% 91% 92% 91% 92% 89% 49% 48% 92% 92% 90%
Table 2: Accuracy scores from previous study.
Table 3 gives the means and standard deviations of algorithm
ranks on the real-world problem set. Note that the standard deviations
are fairly similar.
alg mean stddev
NET 2.24
1.72
FS 3.45
2.20
GP 3.55
2.94
TRE 3.74
1.64
KN 4.39
2.66
MAH 5.03
2.02
DFA 5.11
2.22
NCM 5.47
2.38
KNW 5.74
2.66
REG 5.84
3.38
BAY 6.45
2.55
KWM 6.89
1.89
NC 6.97
2.73
MAJ 8.68
2.24
RND 10.03 1.88
Table 3: Means and standard deviations of
algorithm ranks on real-world problems.
Table 4 shows the results of the four separate analyses
of variance, all of which were highly significant at the 0.05 level.
problem values critical
value F
P
all scores F0.05(1),14,518=1.69
24.8 <0.05
all ranks
F0.05(1),14,518=1.69
32.1 <0.05
real scores F0.05(1),14,392=1.72
17.5 <0.05
real ranks F0.05(1),14,392=1.72
21.6 <0.05
Table 4: Critical values and test statistics for ANOVA.
The results of all pairwise comparisons are shown in Figures 1-4. The algorithms are listed left-to-right in order of decreasing performance. Each horizontal line groups together a set of algorithms which were not found to be significantly different by the Tukey test.
Relative to the corresponding figures in [Majoros 2000], both NET and GP moved left (in the direction of better performance) in all four analyses, with GP moving as many as two positions to the left and NET as many as three. Whereas the leftmost algorithm in all four figures had previously been TRE or FS, it is now uniformly NET.
DFA appears slightly left of center in all four figures,
suggesting that the method is neither the best nor the worst of the algorithms
considered.
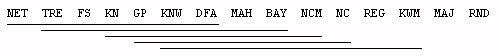
Figure 2. Pairwise comparisons over all problems based on
scores.
Accuracy decreases left-to-right.
![]()
Figure 3. Pairwise comparisons over real-world problems based
on ranks.
Rank increases left-to-right.
![]()
Figure 4. Pairwise comparisons over real-world problems based
on scores.
Accuracy decreases left-to-right.
Ranges of ranks on the real-world problems are shown in
Table 5. GP remains at the same position as in [Majoros 2000], while
NET has moved up one position to the top. Three algorithms that had
previously achieved rank 1 at least once now do no better than rank 2 (NC,
NCM, KWM).
Algorithm Range of ranks
NET
1-6
TRE
1-7
FS
1-9
GP
1-10
KN
1-10
BAY
1-11
KNW
1-11
REG
1-13
NCM
2-9
MAH
2-9
DFA
2-9
KWM
2-10
NC
2-12
--MAJ--------------3-12--
RND
6-13
Table 5: Ranges of ranks on real-world problems.
The dashed line highlights the MAJ baseline.
Table 6 gives the observed frequencies of achieving the
top rank. Note that the frequencies do not sum to 1 because of occasional
ties for the top rank. These frequencies are therefore not (in general)
additive, so the corresponding frequencies for groups of algorithms must
be computed from the original raw scores (see Table 7, below).
Algorithm Frequency
NET
41%
GP
31%
FS
28%
KN
21%
KNW
3%
BAY
3%
REG
3%
TRE
3%
Table 6: Frequency with which an algorithm achieved top rank
on real-world problems.
Table 7 gives the probability (i.e., frequency) of achieving
top rank on the real-world problem set with various groups of algorithms.
These groups were specifically chosen to maximize performance, so that,
for example, no group of size 3 could be found which would have P[#1]>93%.
Thus, achieving top rank with at least 95% confidence would require a suite
of at least four algorithms.
group size P[#1]
group members
1
41%
NET
2
72%
GP+NET
3
93%
FS+GP+NET
4
97%
REG+FS+GP+NET
5
100%
TRE+REG+FS+GP+NET
Table 7: Number of algorithms required to achieve top rank
with the given frequency on
the real-world problem set. P[#1] is the frequency of achieving
top rank.
Table 8 generalizes Table 7 by considering the probability
of achieving first or second rank. As can be seen from the table,
placing first or second on the real-world problem set can be assured by
employing a suite of only three algorithms.
group size P[#1 or #2]
group members
1
69%
NET
2
90%
FS+NET
3
100%
GP+FS+NET
Table 8: Number of algorithms required to achieve first or
second rank with the given
frequency on the real-world problem set. P[#1 or #2] is the
frequency of achieving first
or second rank.
Whereas [Majoros 2000] could not extoll a single algorithm as being clearly superior to all others under consideration, neural networks exhibited remarkable performance in the present study, placing first according to several different criteria. They had the best mean rank (2.24), the best range of ranks (1-6), the best mean accuracy (79%), the highest frequency of top rank (41%), and the highest frequency of ranking first or second (69%).
Nevertheless, backpropagation neural networks still do not qualify as a "silver bullet;" i.e., as an algorithm which produces the highest score on nearly all problems. In fact, on the majority of problems (59%), NET was outperformed by other algorithms.
Thus, it is still apparent that one needs to apply more than one classification method to a new problem if one wishes to be highly confident of achieving the highest possible score. What the present study suggests, however, is that one need only employ a "toolbox" of 4 algorithms (NET,GP,FS,REG) to achieve the highest score with at least 95% confidence, rather than 7 algorithms as suggested previously. Furthermore, using only NET and FS, it seems one can count on achieving nearly maximal performance with 90% confidence. Adding GP to this "toolbox" boosts confidence to 100% (at least on the problem suite used in this study). It therefore seems more reasonable now to suggest that practitioners maintain a toolbox of black-box classifiers for application to novel problems, given that so few classifiers may be needed.
It is interesting to speculate on the significance of linear regression appearing in Table 7. The accuracy scores of this method have not been overly impressive -- indeed, it is the lowest scoring algorithm other than the baselines MAJ and RND on the real-world problem set (see Figure 4). Its importance in reaching 95% confidence in achieving top rank may be due to an inductive bias sufficiently different from other methods such as NET and FS so as to accommodate those few problems handled poorly by the more general methods. That is, feedforward backpropagation neural networks may lack something in their inductive bias relative to selected classification problems that cannot be entirely compensated for by arbitrarily increasing computational effort.
The DFA method has turned out to be rather unremarkable,
being positioned as it is near neither extreme of the performance spectrum.
It is noteworthy, however, that FS ranks significantly better than DFA,
given their similarities. Whereas DFA computes a new set of features
which maximize (subject to linearity constraints) the F ratio of between-group
variance to within-group variance, FS merely sorts the original features
according to their F ratios and discards any feature having a low F ratio
and not contributing to cross-validation accuracy scores. This is
presumably a testament to the importance of the nonlinear relationships
between the original features which are lost through linearization.
Backpropagation neural networks, although not perfectly suited for all problems, have been seen to compete very favorably with other popular algorithms, and can certainly be recommended to practitioners who are compelled to rely on a single tool, so long as their computational resources are not minimal. Given that the hardware used in this study was purchased for under $5000 US, this should not be a limiting factor for most small businesses, especially given the ongoing advances in microprocessor technology and the attendant price reductions that can be expected to continue for the foreseeable future.
[Majoros 2000] Bill Majoros, On Free Lunches
and Silver Bullets: An Empirical Comparison of Seven Machine-Learning
Algorithms for Classification [http://geocities.datacellar.net/ResearchTriangle/Forum/1203/ml_7.html].
[Manly 1994] Bryan F.J. Manly, Multivariate Statistical Methods, Chapman & Hall, 1994.
[Masters 1995] Timothy Masters, Neural, Novel & Hybrid Algorithms for Time Series Prediction, John Wiley & Sons, 1995.
[Murphy and Aha] P. Murphy and D. Aha, UCI Repository of machine learning databases [http://www.ics.uci.edu/~mlearn/MLRepository.html]. Irvine, CA: University of California, Department of Information and Computer Science.
[Zar 1996] Jerrold H. Zar, Biostatistical Analysis,
Prentice Hall, 1996.